 En una publicación anterior escribí sobre la relación entre utilización, fluctuación y tiempo de espera, y su aproximación por la fórmula de kingman . Permítame mostrarle un juego de dados rápido y fácil en el que simulamos un pago en el supermercado para que los participantes experimenten el efecto de la utilización, la fluctuación y el (peor) efecto combinado de ambos.
En una publicación anterior escribí sobre la relación entre utilización, fluctuación y tiempo de espera, y su aproximación por la fórmula de kingman . Permítame mostrarle un juego de dados rápido y fácil en el que simulamos un pago en el supermercado para que los participantes experimenten el efecto de la utilización, la fluctuación y el (peor) efecto combinado de ambos.
Introducción

El tiempo de espera frente a un proceso está fuertemente influenciado por dos cosas: el utilización de un proceso (¿qué tan ocupado está?) y el fluctuaciones de los tiempos de llegada y proceso (¿qué tan estable es el sistema, o no?). La ecuación de Kingman y otros lo muestran muy bien (consulte mi publicación La fórmula de Kingman: variación, utilización y tiempo de entrega para obtener detalles sobre la ecuación). A medida que la utilización se acerca al 100%, el tiempo de espera se acerca al infinito. A medida que aumentan las fluctuaciones de los tiempos de llegada y proceso, también aumenta el tiempo de espera. Este juego demostrará este efecto.
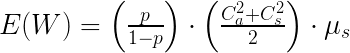
Equipo de juego

¡Lo que necesitas son dados! ¡Dados de muchos lados diferentes! Si creciste antes de internet como yo, entonces puedes estar familiarizado con los dados que son diferentes de los dados comunes de seis lados D6 (¿Alguien de mazmorras y dragones?). En particular, necesita tres tipos diferentes de dados: uno pequeño (D4 o D6), uno mediano (D10 o D12) y uno grande (D20 o D30).
Idealmente, tiene uno de cada dado por cada jugador, pero si tiene pocos dados, puede tener un dado por cada dos jugadores (en breve formaremos equipos de dos personas). Es mejor tener una gran extensión en el rango de dados (es decir, usar D4 como el más pequeño y D30 como el más grande).
Te Puede Interesar
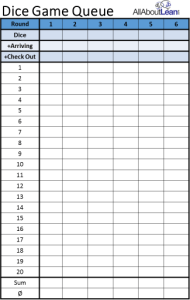 Luego, necesitaría imprimir las hojas de datos (una por cada dos jugadores, y tal vez algunas para hacer una copia de seguridad). También hay una hoja de descripción general, pero también puede usar una pizarra, una pizarra o un rotafolio para un boceto rápido. Más sobre esto a continuación.
Luego, necesitaría imprimir las hojas de datos (una por cada dos jugadores, y tal vez algunas para hacer una copia de seguridad). También hay una hoja de descripción general, pero también puede usar una pizarra, una pizarra o un rotafolio para un boceto rápido. Más sobre esto a continuación.
El juego en sí dura aproximadamente una hora, incluida cierta teoría, y puede manejar una amplia gama de tamaños de grupos, aunque se vuelve engorroso si tienes más de treinta personas.
El juego
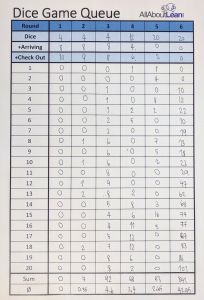
Creará grupos de dos personas, cada una simulando un pago en el supermercado. Uno determinará la cantidad de personas que llegarán, el otro la capacidad de pago. Obtienen una hoja de longitud de la cola del juego de dados como se muestra arriba. Cada uno obtiene un dado, que determinará la cantidad de clientes que llegan al proceso de pago y la cantidad de clientes procesados en el proceso de pago. Es posible que tengan que compartir un dado si le faltan dados. Habrá seis rondas en el juego, y cada ronda consta de veinte iteraciones. En las primeras tres rondas variamos la utilización.
Utilización variable
Ronda 1 – D4 con Offset 2: En la primera ronda, cada jugador obtiene un dado de cuatro lados. Por la cantidad de personas que llegan, tiramos el dado y agregar 13. Por la capacidad de pago, también lanzamos un dado, pero esta vez agregar 15. Por lo tanto, el proceso de pago tiene en promedio dos capacidad más que la cantidad de personas que llegan. Esta información también sería las primeras tres filas vacías en la hoja de datos, donde escribimos 4 (para los lados del dado), 13 (para el cliente) y 15 (para el proveedor). Esto también podría imprimirse en la hoja, pero prefiero mantener a los jugadores en la oscuridad en las rondas futuras para que puedan centrarse en la ronda actual.
Ambos tiran el dado y suman para determinar las llegadas y la capacidad. Si la capacidad coincide o excede la demanda, los dos jugadores escriben un cero en la siguiente celda a continuación. Si las llegadas superan la capacidad, se anota el número de personas que esperan. Estas personas que esperan en la cola deben procesarse en la próxima iteración. Repiten esto durante veinte iteraciones, siempre haciendo un seguimiento de la cantidad de personas que esperan en la fila. Luego calculan la longitud total y promedio de la cola al sumar las veinte entradas y dividirlas por 20. Esto se escribe en las últimas dos filas de la hoja.
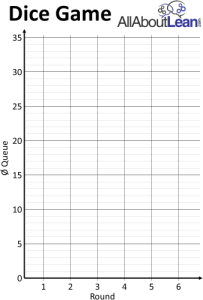 Los resultados se agregan a una estadística general para todos los equipos. Aquí se muestra una hoja en blanco, que podría imprimirse o simplemente dibujarse en una pizarra, pizarra o rotafolio. Anote la longitud promedio de la cola para cada equipo en la ronda 1. Con toda probabilidad, no habrá cola, ya que el resultado esperado es 0.07 personas esperando en línea con una desviación estándar de 0.08 personas.
Los resultados se agregan a una estadística general para todos los equipos. Aquí se muestra una hoja en blanco, que podría imprimirse o simplemente dibujarse en una pizarra, pizarra o rotafolio. Anote la longitud promedio de la cola para cada equipo en la ronda 1. Con toda probabilidad, no habrá cola, ya que el resultado esperado es 0.07 personas esperando en línea con una desviación estándar de 0.08 personas.
Ronda 2 – D4 con Offset 1: La siguiente ronda reducimos el desplazamiento. Los recién llegados continúan agregando 13 al dado, pero el pago ahora agrega 14 (en lugar de 15) a su lanzamiento. Por lo tanto, las primeras tres filas de la ronda 2 son 4, 13 y 14. Nuevamente juegan durante veinte iteraciones y luego determinan la longitud promedio de la cola. Estos resultados se agregarán a las estadísticas generales de todos los equipos.
El resultado esperado ahora es una cola promedio de 0.5 personas con una desviación estándar de 0.4 personas, por lo que habrá más personas esperando en la fila.
Ronda 3 – D4 con Offset 0: La siguiente ronda eliminamos la diferencia entre las llegadas y las salidas. Ambos pueden agregar solo 13 a su lanzamiento de dados. Ahora la cola comienza a calentarse. El resultado esperado es una cola promedio de 3,1 personas con una desviación estándar de 2,3 personas.
Teoría sobre la utilización
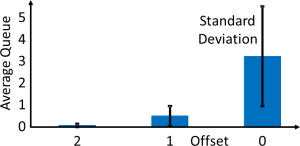 En este punto, deberíamos discutir con los participantes lo que sucedió. Al reducir el exceso de capacidad por iteración de 2 a 1 a 0, en efecto aumentamos la utilización de la comprobación. Cuando el proceso de pago tenía en promedio dos capacidad más que las personas que llegaban, tenía una utilización del 88,57%. Con una compensación de 1, la utilización fue del 93.945%. Sin compensación alguna, la utilización fue del 100%. A la larga, una utilización del 100% significa una longitud de cola infinita, pero como solo hicimos veinte iteraciones, no llegamos tan lejos. Los gráficos muestran los resultados promedio esperados con las desviaciones estándar para un D4 con diferentes compensaciones.
En este punto, deberíamos discutir con los participantes lo que sucedió. Al reducir el exceso de capacidad por iteración de 2 a 1 a 0, en efecto aumentamos la utilización de la comprobación. Cuando el proceso de pago tenía en promedio dos capacidad más que las personas que llegaban, tenía una utilización del 88,57%. Con una compensación de 1, la utilización fue del 93.945%. Sin compensación alguna, la utilización fue del 100%. A la larga, una utilización del 100% significa una longitud de cola infinita, pero como solo hicimos veinte iteraciones, no llegamos tan lejos. Los gráficos muestran los resultados promedio esperados con las desviaciones estándar para un D4 con diferentes compensaciones.
Fluctuación variable
En las siguientes dos rondas, variamos las fluctuaciones mientras mantenemos el desplazamiento constante. Esto significa que la utilización siempre será del 88,57%.
Ronda 4 – D12 con Offset 2: Ahora usamos un dado de doce lados. Los arribos suman 9 a su lanzamiento, y la salida agrega 11 a su lanzamiento. Nuevamente, después de veinte iteraciones, agregamos los promedios a la hoja de resumen. El resultado esperado es una longitud promedio de cola de 3.0 personas, con una desviación estándar de 2.4.
Ronda 5 – D30 con Offset 2: Finalmente, podemos usar el dado de treinta lados. Para mantener la misma utilización y compensación, los arribos no agregan nada a su lanzamiento de dado, mientras que el pago agrega 2 a cada lanzamiento de dado. El resultado esperado es una longitud de cola promedio de 14.7 personas, con una desviación estándar de 11.0.
Teoría de la fluctuación
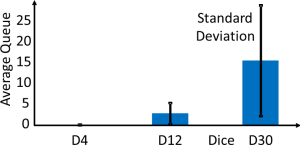 Al cambiar el dado de un D4 a un D12 a un D30 mientras se mantienen constantes las llegadas promedio y la capacidad de salida, en realidad aumentamos la fluctuación. Las llegadas D4 +13 significaron que el número de llegadas fluctuó entre 14 y 17 con un promedio de 15.5. Un D12 +9 mantiene el mismo promedio de 15.5, pero ahora con una fluctuación de 10 a 21. Un D30 más nada nuevamente tiene el mismo promedio de 15.5, pero ahora fluctúa entre 1 y 30.
Al cambiar el dado de un D4 a un D12 a un D30 mientras se mantienen constantes las llegadas promedio y la capacidad de salida, en realidad aumentamos la fluctuación. Las llegadas D4 +13 significaron que el número de llegadas fluctuó entre 14 y 17 con un promedio de 15.5. Un D12 +9 mantiene el mismo promedio de 15.5, pero ahora con una fluctuación de 10 a 21. Un D30 más nada nuevamente tiene el mismo promedio de 15.5, pero ahora fluctúa entre 1 y 30.
Por lo tanto, aumentamos la utilización. Similar a la utilización, el aumento de la fluctuación también aumentó el retraso acumulado promedio como se muestra en el cuadro anterior.
Utilización y fluctuación variables
Ronda 6 – D30 con Offset 0: Para la próxima ronda aumentamos tanto la fluctuación como la utilización. Tanto las llegadas como la salida obtienen un dado de treinta lados, y ninguno de los dos agrega nada al lanzamiento del dado. Importante: Antes de que hagamos esta ronda, ¡pregunte a los participantes sobre sus suposiciones sobre cuánto tiempo durará la fila! Con toda probabilidad, probablemente agregarán los dos efectos juntos y esperarán una longitud de cola de alrededor de 18. Sin embargo, lo que no saben (todavía) es que estos efectos no son aditivos sino más multiplicativos. Hagamos la sexta ronda.
La longitud esperada de la cola no es 18, sino 24.2 personas, con una desviación estándar de 17.6. Por lo tanto, es mucho más grande de lo esperado. Haga hincapié en que esto no es aditivo sino multiplicativo según la ecuación de Kingman anterior.
Simulación de resultados esperados

Para su conveniencia, aquí hay una tabla de los resultados esperados para las compensaciones 2, 1 y 0 y para los dados de dos lados (un lanzamiento de moneda) a treinta lados en pasos de dos basados en doscientos juegos cada uno. Naturalmente, hice esto en Excel en lugar de tirar un dado dieciocho mil veces. Además, no tengo un dado de veintiséis caras, que según Wikipedia no sería realmente un buen dado de todos modos. En cualquier caso, aquí está la media y la desviación estándar de la longitud de la cola para diferentes situaciones.
| Longitud media de la cola |
Desviación estándar de la longitud de la cola |
|||||
| Dado | Offset 2 | Offset 1 | Offset 0 | Offset 2 | Offset 1 | Offset 0 |
| 2 | 0,00 | 0,00 | 1,21 | 0,00 | 0,00 | 0,88 |
| 4 4 | 0,07 | 0,49 | 3,07 | 0,08 | 0,42 | 2,28 |
| 6 6 | 0,47 | 1,35 | 4,80 | 0,39 | 1,11 | 3,59 |
| 8 | 1,01 | 2,89 | 5,80 | 0,79 | 2,99 | 4,03 |
| 10 | 1,88 | 3,86 | 7,70 | 1,50 | 3,35 | 5,48 |
| 12 | 2,98 | 5,39 | 10,26 | 2,44 | 4,45 | 7,25 |
| 14 | 3,91 | 6,83 | 11,71 | 3,33 | 5,75 | 7,90 |
| dieciséis | 5,49 | 7,33 | 13,24 | 4,88 | 5,32 | 8,60 |
| 18 años | 6,04 | 9,56 | 14,62 | 4,93 | 7,42 | 10,35 |
| 20 | 8,22 | 11,99 | 15,67 | 6,95 | 9,26 | 11,83 |
| 22 | 9,85 | 12,33 | 19,17 | 8,23 | 9,19 | 13,67 |
| 24 | 10,92 | 14,19 | 20,51 | 9,39 | 10,56 | 14,30 |
| 26 | 12,44 | 16,99 | 23,02 | 10,92 | 11,70 | 16,17 |
| 28 | 11,89 | 18,65 | 22,83 | 9,13 | 13,44 | 15,75 |
| 30 | 14,70 | 20,36 | 24,18 | 11,02 | 14,49 | 17,64 |
[post_relacionado id=»608″]
Dados diferentes
 Si no tiene un dado de treinta lados, también puede usar un dado de veinte lados. Si su dado más grande tiene solo doce lados, entonces puede ser difícil ver un buen efecto. Los números agregados a las llegadas para diferentes dados anteriores funcionarían para cualquier dado de hasta 30, pero si tiene dados más pequeños, también puede usar complementos más pequeños. La siguiente tabla muestra la cantidad que se debe agregar a las llegadas para diferentes dados dependiendo de su dado más grande. Los números en cualquier fila también funcionarían para cualquier dado más pequeño. El pago debe agregar 2, 1 o 0 en la parte superior dependiendo de la utilización que desee.
Si no tiene un dado de treinta lados, también puede usar un dado de veinte lados. Si su dado más grande tiene solo doce lados, entonces puede ser difícil ver un buen efecto. Los números agregados a las llegadas para diferentes dados anteriores funcionarían para cualquier dado de hasta 30, pero si tiene dados más pequeños, también puede usar complementos más pequeños. La siguiente tabla muestra la cantidad que se debe agregar a las llegadas para diferentes dados dependiendo de su dado más grande. Los números en cualquier fila también funcionarían para cualquier dado más pequeño. El pago debe agregar 2, 1 o 0 en la parte superior dependiendo de la utilización que desee.
| Dado | D4 | D6 | D8 | D10 | D12 | D20 | D30 |
| Max D30 | 13 | 12 | 11 | 10 | 9 9 | 5 5 | 0 0 |
| Max D20 | 8 | 7 7 | 6 6 | 5 5 | 4 4 | 0 0 | |
| Max D12 | 4 4 | 3 | 2 | 1 | 0 0 |
Entonces, ahí está, ¡un juego rápido y fácil con el que puedes demostrar el efecto en la acumulación o el tiempo de espera de la utilización y la fluctuación, y el efecto combinado mucho peor de la utilización y la fluctuación! Creo que todos pueden compartir ese sentimiento si están esperando en la caja del supermercado.
Este juego se inspiró en el juego de dados en The Lean Games and Simulations Book de John Bicheno, que usa D6 para mostrar el efecto de la utilización. Expandí esto usando diferentes dados para mostrar también el efecto de la fluctuación y el efecto combinado aún peor. Ahora, ¡salga, tire un dado (no a su compañero de trabajo, jefe o cliente), reduzca la fluctuación, controle la utilización y organice su industria!







