Convection for Straight Fin Formulae and Calculator

Convection for Straight Fin Formulae and Calculator is a crucial tool for engineers and researchers to calculate heat transfer rates from straight fins. The straight fin is a common geometry used in various heat exchangers, and understanding its convective behavior is essential for designing efficient thermal systems. This article provides a comprehensive overview of the formulae and equations used to calculate convective heat transfer from straight fins, along with a calculator to simplify the process. The calculator uses established methods to determine the heat transfer rate.
Convection for Straight Fin Formulae and Calculator
The concept of convection in straight fins is crucial in understanding heat transfer and designing efficient heat exchangers. Convection occurs when there is a temperature difference between the fin and the surrounding fluid, causing the fluid to move and transfer heat. The heat transfer coefficient (h) is a key parameter in determining the rate of convection.
Introduction to Convection in Straight Fins
Convection in straight fins is a complex phenomenon that involves the movement of fluid over the surface of the fin. The Reynolds number (Re) plays a significant role in determining the nature of the flow, whether it is laminar or turbulent. The Nusselt number (Nu) is another important parameter that characterizes the convective heat transfer.
Formulae for Convection in Straight Fins
The Newton's law of cooling states that the rate of heat transfer (Q) is proportional to the temperature difference (ΔT) between the fin and the surrounding fluid. The formula for convection in straight fins is given by: Q = h A ΔT, where A is the surface area of the fin. The convective heat transfer coefficient (h) can be calculated using the Dittus-Boelter equation or the Colburn equation.
| Formula | Description |
|---|---|
| Q = h A ΔT | Newton's law of cooling |
| h = 0.023 (k / D) Re^0.8 Pr^0.33 | Dittus-Boelter equation |
| h = 0.023 (k / D) Re^0.8 (Pr / Pr_w)^0.25 | Colburn equation |
Calculator for Convection in Straight Fins
A calculator for convection in straight fins can be designed using the above formulae. The input parameters include the length and width of the fin, the temperature difference, and the properties of the fluid. The output parameters include the rate of heat transfer, the convective heat transfer coefficient, and the efficiency of the fin.
Applications of Convection in Straight Fins
Convection in straight fins has numerous applications in engineering, including the design of heat exchangers, cooling systems, and electronic devices. The optimization of fin geometry and material can significantly improve the performance of these systems. The analysis of convection in straight fins can also be used to predict the thermal performance of complex systems.
Limitations and Future Directions
The limitations of the current formulae and calculators for convection in straight fins include the assumption of steady-state conditions and the neglect of radiation effects. Future research directions include the development of transient models and the incorporation of radiative heat transfer. The use of computational fluid dynamics (CFD) and machine learning algorithms can also improve the accuracy and efficiency of convective heat transfer calculations. Experimental studies can provide valuable insights into the physics of convection in straight fins and validate the theoretical models.
What is the formula for calculating convection?
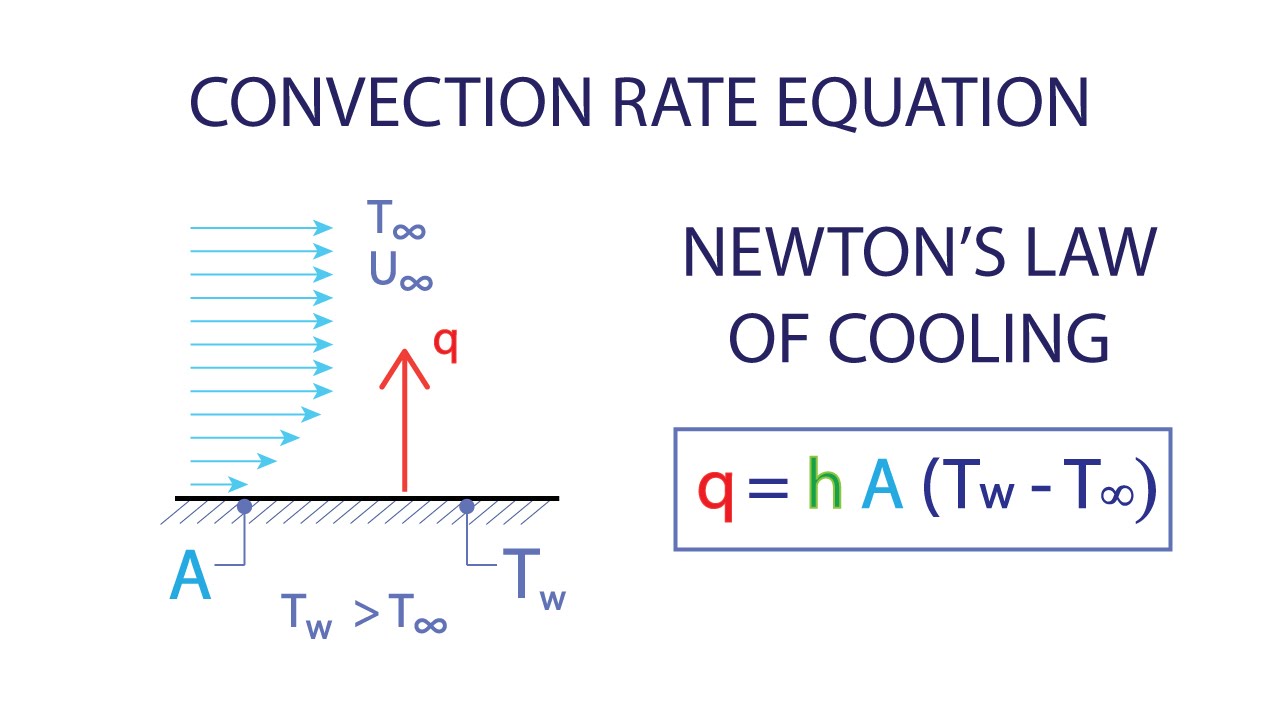
The formula for calculating convection is based on the heat transfer equation, which is given by Q = h A (T1 - T2), where Q is the heat flux, h is the convective heat transfer coefficient, A is the surface area, and T1 and T2 are the temperatures of the two surfaces. This equation is used to calculate the rate of heat transfer due to convection.
Introduction to Convection
Convection is a mode of heat transfer that occurs through the movement of fluids. The formula for calculating convection is based on the heat transfer equation, which takes into account the convective heat transfer coefficient, surface area, and temperature difference. The key factors that affect convection are:
- Fluid velocity: The speed at which the fluid is moving
- Fluid properties: The density, viscosity, and specific heat capacity of the fluid
- Surface roughness: The roughness of the surface can affect the convective heat transfer coefficient
Convective Heat Transfer Coefficient
The convective heat transfer coefficient (h) is a critical parameter in the calculation of convection. It depends on the fluid properties, flow velocity, and surface roughness. The convective heat transfer coefficient can be calculated using various correlations and empirical formulas, which are based on experimental data. The key factors that affect the convective heat transfer coefficient are:
- Fluid type: The type of fluid, such as air, water, or oil, affects the convective heat transfer coefficient
- Flow regime: The flow regime, such as laminar or turbulent, affects the convective heat transfer coefficient
- Surface geometry: The shape and size of the surface affect the convective heat transfer coefficient
Surface Area and Temperature Difference
The surface area (A) and temperature difference (T1 - T2) are also important parameters in the calculation of convection. The surface area affects the heat flux, while the temperature difference drives the heat transfer. The key factors that affect the surface area and temperature difference are:
- Geometry: The shape and size of the surface affect the surface area
- Material properties: The thermal conductivity and specific heat capacity of the material affect the temperature difference
- Boundary conditions: The boundary conditions, such as insulated or constant temperature, affect the temperature difference
Types of Convection
There are two main types of convection: natural convection and forced convection. Natural convection occurs due to the density difference between the fluid and the surrounding environment, while forced convection occurs due to an external force, such as a fan or pump. The key factors that affect the type of convection are:
- Fluid properties: The density, viscosity, and specific heat capacity of the fluid affect the type of convection
- Flow velocity: The speed at which the fluid is moving affects the type of convection
- Surface geometry: The shape and size of the surface affect the type of convection
Applications of Convection
Convection has various applications in engineering and science, such as heat exchangers, air conditioning, and weather forecasting. The formula for calculating convection is used to design and optimize these systems. The key factors that affect the applications of convection are:
- Energy efficiency: The heat transfer coefficient and surface area affect the energy efficiency of the system
- Cost: The cost of the system and the materials used affect the application of convection
- Performance: The performance of the system, such as the heat flux and temperature difference, affects the application of convection
How to calculate heat transfer due to convection?

To calculate heat transfer due to convection, you need to consider the convection coefficient, fluid properties, and temperature differences. The convection coefficient, also known as the heat transfer coefficient, is a measure of the ability of a fluid to transfer heat through convection. The calculation involves determining the Nusselt number, Reynolds number, and Prandtl number, which are dimensionless quantities that characterize the convective heat transfer process.
Understanding Convection Heat Transfer
Convection heat transfer occurs when a fluid flows over a surface, causing heat to be transferred between the surface and the fluid. This type of heat transfer is commonly observed in natural convection, where a fluid rises due to density differences caused by temperature gradients. To calculate convection heat transfer, you need to understand the mechanisms of heat transfer, including conduction, convection, and radiation.
- Identify the type of convection: forced convection or natural convection
- Determine the fluid properties: density, viscosity, specific heat capacity, and thermal conductivity
- Calculate the Reynolds number to determine the flow regime: laminar or turbulent
Calculating Convection Heat Transfer Coefficient
The convection heat transfer coefficient, also known as the film coefficient, is a measure of the ability of a fluid to transfer heat through convection. This coefficient depends on the fluid properties, flow velocity, and surface roughness. To calculate the convection heat transfer coefficient, you can use empirical correlations or numerical methods.
- Choose a suitable correlation: Dittus-Boelter equation or Colburn equation
- Determine the fluid properties: density, viscosity, specific heat capacity, and thermal conductivity
- Calculate the Nusselt number to determine the convection heat transfer coefficient
Factors Affecting Convection Heat Transfer
Several factors can affect convection heat transfer, including fluid properties, flow velocity, surface roughness, and temperature differences. Understanding these factors is crucial to accurately calculating convection heat transfer.
- Fluid properties: density, viscosity, specific heat capacity, and thermal conductivity
- Flow velocity: laminar or turbulent flow
- Surface roughness: smooth or rough surface
Applications of Convection Heat Transfer
Convection heat transfer has numerous practical applications, including heat exchangers, cooling systems, and thermal management. Understanding convection heat transfer is essential to designing efficient and effective thermal systems.
- Heat exchangers: plate heat exchangers or tube heat exchangers
- Cooling systems: air cooling or liquid cooling
- Thermal management: electronics cooling or building insulation
Challenges in Calculating Convection Heat Transfer
Calculating convection heat transfer can be challenging due to the complexity of fluid flow and heat transfer mechanisms. Numerical methods, such as computational fluid dynamics, can be used to simulate convection heat transfer and provide accurate results.
- Complexity of fluid flow: turbulent flow or multiphase flow
- Heat transfer mechanisms: conduction, convection, and radiation
- Numerical methods: finite element method or finite volume method
What is the formula for convection in a pipe?

The formula for convection in a pipe is a complex equation that takes into account several factors, including the velocity of the fluid, the temperature difference between the fluid and the pipe, and the properties of the fluid and the pipe. The most common formula used to describe convection in a pipe is the Nusselt number equation, which is given by: Nu = (h D) / k, where Nu is the Nusselt number, h is the convective heat transfer coefficient, D is the diameter of the pipe, and k is the thermal conductivity of the fluid.
Introduction to Convection in a Pipe
Convection in a pipe is a type of heat transfer that occurs when a fluid flows through a pipe and transfers heat to or from the pipe wall. The formula for convection in a pipe is used to calculate the rate of heat transfer and to design heat exchangers and other equipment. The key factors that affect convection in a pipe are the velocity of the fluid, the temperature difference between the fluid and the pipe, and the properties of the fluid and the pipe. Some of the key concepts related to convection in a pipe include:
- Laminar flow: a type of fluid flow in which the fluid flows in parallel layers, with no turbulence or mixing between the layers.
- Turbulent flow: a type of fluid flow in which the fluid flows in a chaotic, irregular manner, with mixing and turbulence between the layers.
- Conductive heat transfer: a type of heat transfer that occurs through direct contact between particles or molecules.
Factors Affecting Convection in a Pipe
The formula for convection in a pipe is affected by several factors, including the velocity of the fluid, the temperature difference between the fluid and the pipe, and the properties of the fluid and the pipe. The velocity of the fluid is a key factor, as it determines the rate of heat transfer and the amount of heat transferred. The temperature difference between the fluid and the pipe is also important, as it drives the heat transfer process. Some of the key factors that affect convection in a pipe include:
- Fluid properties: such as density, viscosity, and thermal conductivity, which affect the rate of heat transfer and the amount of heat transferred.
- Pipe properties: such as diameter, length, and material, which affect the rate of heat transfer and the amount of heat transferred.
- Flow regime: whether the flow is laminar or turbulent, which affects the rate of heat transfer and the amount of heat transferred.
Applications of Convection in a Pipe
The formula for convection in a pipe has many practical applications, including the design of heat exchangers, boilers, and condensers. Convection in a pipe is also important in chemical processing, power generation, and refrigeration. Some of the key applications of convection in a pipe include:
- Heat exchangers: devices that transfer heat from one fluid to another, often using convection to enhance the heat transfer process.
- Boilers: devices that use convection to transfer heat from a fuel source to a fluid, producing steam or hot water.
- Condensers: devices that use convection to transfer heat from a fluid to a cooling medium, often using water or air as the cooling medium.
Calculating Convection in a Pipe
To calculate convection in a pipe, the Nusselt number equation is often used, which is given by: Nu = (h D) / k, where Nu is the Nusselt number, h is the convective heat transfer coefficient, D is the diameter of the pipe, and k is the thermal conductivity of the fluid. Some of the key steps involved in calculating convection in a pipe include:
- Determining the flow regime: whether the flow is laminar or turbulent, which affects the rate of heat transfer and the amount of heat transferred.
- Calculating the convective heat transfer coefficient: using the Nusselt number equation or other correlations, such as the Dittus-Boelter correlation.
- Calculating the heat transfer rate: using the convective heat transfer coefficient and the temperature difference between the fluid and the pipe.
Challenges and Limitations of Convection in a Pipe
There are several challenges and limitations associated with convection in a pipe, including the complexity of the flow regime, the uncertainty of the fluid properties, and the difficulty of measuring the convective heat transfer coefficient. Some of the key challenges and limitations include:
- Flow regime: the flow regime can be laminar or turbulent, which affects the rate of heat transfer and the amount of heat transferred.
- Fluid properties: the fluid properties, such as density, viscosity, and thermal conductivity, can be uncertain or difficult to measure.
- Measurement uncertainty: the measurement uncertainty of the convective heat transfer coefficient and other parameters can be high, which affects the accuracy of the calculations.
What is the rate equation for convection?

The rate equation for convection is a mathematical representation of the convective heat transfer process, which occurs when there is a fluid in motion over a surface. The rate equation for convection is given by the Newton's law of cooling, which states that the rate of heat transfer is proportional to the temperature difference between the fluid and the surface. The equation is:
Q = h A (T_s - T_f)
where Q is the heat transfer rate, h is the convective heat transfer coefficient, A is the surface area, T_s is the surface temperature, and T_f is the fluid temperature.
What is the convective heat transfer coefficient?
The convective heat transfer coefficient is a measure of the ability of the fluid to transfer heat to or from the surface. It depends on various factors, such as the velocity of the fluid, the properties of the fluid, and the geometry of the surface. The convective heat transfer coefficient can be calculated using empirical correlations or numerical simulations. Some of the key factors that affect the convective heat transfer coefficient are:
- The Reynolds number, which is a measure of the turbulence of the fluid flow
- The Prandtl number, which is a measure of the thermal conductivity of the fluid
- The Nusselt number, which is a measure of the heat transfer between the fluid and the surface
What are the types of convective heat transfer?
There are two main types of convective heat transfer: forced convection and natural convection. Forced convection occurs when the fluid is pumped or blown over the surface, while natural convection occurs when the fluid is stationary and the heat transfer occurs due to density gradients. The type of convective heat transfer that occurs depends on the velocity of the fluid and the temperature difference between the fluid and the surface. Some of the key differences between forced and natural convection are:
- The velocity of the fluid, which is higher in forced convection than in natural convection
- The heat transfer coefficient, which is higher in forced convection than in natural convection
- The flow regime, which can be laminar or turbulent in forced convection, and is usually laminar in natural convection
What are the applications of convective heat transfer?
Convective heat transfer has numerous applications in various fields, such as engineering, chemistry, and physics. Some of the key applications of convective heat transfer are:
- Heat exchangers, which are used to transfer heat between two fluids
- Refrigeration systems, which use convective heat transfer to cool fluids
- Power plants, which use convective heat transfer to transfer heat from the combustion chamber to the steam generator
What are the limitations of convective heat transfer?
Convective heat transfer has several limitations, such as the low heat transfer rates and the complexity of the flow regime. Some of the key limitations of convective heat transfer are:
- The heat transfer coefficient, which can be low in certain flow regimes
- The flow regime, which can be complex and difficult to predict
- The surface roughness, which can enhance or reduce the heat transfer rate
How is convective heat transfer modeled?
Convective heat transfer can be modeled using various mathematical and numerical techniques, such as the finite element method and the computational fluid dynamics. Some of the key techniques used to model convective heat transfer are:
- The Navier-Stokes equations, which are used to simulate the fluid flow
- The energy equation, which is used to simulate the heat transfer
- The turbulence models, which are used to simulate the turbulent flow regime
Frequently Asked Questions (FAQs)
What is Convection for Straight Fin Formulae and Calculator?
Convection for straight fin formulae and calculator is a mathematical model used to calculate the heat transfer from a straight fin to the surrounding environment. The formulae take into account various parameters such as the fin length, fin thickness, thermal conductivity, and convective heat transfer coefficient. The calculator is a tool that simplifies the calculation process, allowing users to input the relevant parameters and obtain the result. The convection for straight fin formulae and calculator is widely used in engineering and design applications, particularly in the fields of mechanical engineering, aerospace engineering, and chemical engineering. The formulae and calculator are essential for optimizing the design of straight fins, which are commonly used in heat exchangers, radiators, and electronic devices.
How to Use the Convection for Straight Fin Formulae and Calculator?
To use the convection for straight fin formulae and calculator, users need to input the relevant parameters such as the fin length, fin thickness, thermal conductivity, convective heat transfer coefficient, and ambient temperature. The formulae are based on the theory of heat transfer, which states that the heat transfer rate is proportional to the temperature difference between the fin and the surrounding environment. The calculator uses these formulae to calculate the heat transfer rate, fin efficiency, and fin effectiveness. Users can select the units of measurement and the calculation options to obtain the desired results. The convection for straight fin formulae and calculator also provide graphs and charts to visualize the results, making it easier to analyze and optimize the design of straight fins.
What are the Applications of Convection for Straight Fin Formulae and Calculator?
The convection for straight fin formulae and calculator have a wide range of applications in various fields of engineering and design. One of the primary applications is in the design of heat! exchangers, where straight fins are used to enhance the heat transfer between two fluids. The formulae and calculator are also used in the design of radiators, where straight fins are used to dissipate the heat generated by electronic devices. Additionally, the convection for straight fin formulae and calculator are used in aerospace engineering to analyze the heat transfer from aircraft and spacecraft. The formulae and calculator are also used in chemical engineering to design and optimize the heat transfer in chemical reactors and process equipment. The convection for straight fin formulae and calculator are essential tools for engineers and designers to optimize the performance and efficiency of straight fins.
What are the Limitations of Convection for Straight Fin Formulae and Calculator?
The convection for straight fin formulae and calculator have some limitations that need to be considered. One of the main limitations is that the formulae assume a steady-state condition, which may not be valid in all situations. The formulae also assume a uniform convective heat transfer coefficient, which may not be accurate in all cases. Additionally, the formulae do not take into account the effects of radiation and conduction, which can be significant in some applications. The calculator also has some limitations, such as the rounding errors and truncation errors, which can affect the accuracy of the results. Furthermore, the convection for straight fin formulae and calculator are based on simplifying assumptions, such as the fin being straight and uniform, which may not be valid in all cases. Therefore, users need to be aware of these limitations and use the formulae and calculator with caution and judgment.
Deja una respuesta

Entradas Relacionadas