Volume and Area of Sphere Equation and Calculator

The equations for calculating the volume and area of a sphere are fundamental concepts in geometry and mathematics. A sphere is a perfectly symmetrical three-dimensional shape, and its volume and surface area can be calculated using specific formulas. The volume of a sphere is given by the equation V = (4/3)πr³, where r is the radius of the sphere. The surface area of a sphere is calculated using the equation A = 4πr². These equations are essential in various fields, including physics, engineering, and architecture, and are used to solve problems involving spherical shapes.
- Understanding the Volume and Area of a Sphere: Equations and Calculators
- How do you find the area and volume of a sphere?
- What is the formula for sphere and volume?
- Why is 4:3 used in the volume of a sphere?
- What is the formula for the area of a sphere?
-
Frequently Asked Questions (FAQs)
- What is the formula for calculating the volume and area of a sphere?
- How does the volume and area of a sphere calculator work?
- What are the real-world applications of calculating the volume and area of a sphere?
- How can I use the volume and area of a sphere equation and calculator for educational purposes?
Understanding the Volume and Area of a Sphere: Equations and Calculators
The volume and area of a sphere are fundamental concepts in geometry and are used in various fields such as physics, engineering, and architecture. The volume of a sphere is the amount of space inside the sphere, while the surface area is the total area of the sphere's surface. To calculate these values, we use specific equations that involve the sphere's radius or diameter.
Introduction to Sphere Volume and Area Formulas
The formula for the volume of a sphere is ( V = frac{4}{3} pi r^3 ), where ( r ) is the radius of the sphere. The surface area of a sphere is given by ( A = 4 pi r^2 ). These formulas are derived from the geometry of the sphere and are used in calculations to determine the volume and surface area of spheres in various applications.
How to Calculate the Volume of a Sphere
To calculate the volume of a sphere, you need to know the radius of the sphere. Once you have the radius, you can plug it into the volume formula and perform the necessary calculations. For example, if the radius of the sphere is 5 units, the volume would be ( V = frac{4}{3} pi (5)^3 ). This calculation yields the volume of the sphere in cubic units.
Understanding the Surface Area of a Sphere
The surface area of a sphere is a measure of the total area of its surface. It is calculated using the formula ( A = 4 pi r^2 ), where ( r ) is the radius of the sphere. The surface area is important in various applications, such as determining the amount of material needed to cover the surface of a sphere or calculating the drag force on a spherical object moving through a fluid.
Applications of Sphere Volume and Area Calculations
The calculations of the volume and surface area of a sphere have numerous applications in science and engineering. For example, in physics, the volume and surface area of a sphere are used to calculate the moment of inertia and the surface tension of the sphere. In engineering, these calculations are used in the design of spherical tanks, domes, and other structures.
Using a Sphere Volume and Area Calculator
A calculator for the volume and surface area of a sphere can simplify the calculation process. These calculators typically require the user to input the radius or diameter of the sphere and then perform the necessary calculations to display the volume and surface area. Some calculators may also provide additional features, such as graphs or tables, to help users understand the relationships between the radius, volume, and surface area of a sphere.
| Radius | Volume | Surface Area |
|---|---|---|
| 5 units | ( frac{4}{3} pi (5)^3 ) | ( 4 pi (5)^2 ) |
| 10 units | ( frac{4}{3} pi (10)^3 ) | ( 4 pi (10)^2 ) |
How do you find the area and volume of a sphere?

To find the area and volume of a sphere, you need to use specific formulas. The area of a sphere is given by the formula 4 π r^2, where r is the radius of the sphere. The volume of a sphere is given by the formula (4/3) π r^3, where r is the radius of the sphere. These formulas are used to calculate the surface area and volume of a sphere, which is a three-dimensional shape that is perfectly round.
Understanding the Formulas for Area and Volume
To calculate the area and volume of a sphere, you need to understand the formulas and how to apply them. Here are the steps to follow:
- Identify the radius of the sphere, which is the distance from the center of the sphere to its surface.
- Use the formula 4 π r^2 to calculate the area of the sphere.
- Use the formula (4/3) π r^3 to calculate the volume of the sphere.
The formulas for area and volume of a sphere are based on the mathematical concept of pi (π) and the radius of the sphere.
Calculating the Surface Area of a Sphere
The surface area of a sphere is the total area of its surface. To calculate the surface area, you need to use the formula 4 π r^2, where r is the radius of the sphere. Here are the steps to follow:
- Identify the radius of the sphere.
- Plug in the value of the radius into the formula 4 π r^2.
- Calculate the surface area using the formula.
The surface area of a sphere is an important concept in mathematics and physics, and is used to calculate the area of spherical shapes.
Calculating the Volume of a Sphere
The volume of a sphere is the amount of space it occupies. To calculate the volume, you need to use the formula (4/3) π r^3, where r is the radius of the sphere. Here are the steps to follow:
- Identify the radius of the sphere.
- Plug in the value of the radius into the formula (4/3) π r^3.
- Calculate the volume using the formula.
The volume of a sphere is an important concept in mathematics and physics, and is used to calculate the volume of spherical shapes.
Real-World Applications of Spheres
Spheres have many real-world applications in science, engineering, and architecture. Here are some examples:
- Balls and spheres are used in sports and games.
- Spherical shapes are used in architecture to design buildings and structures.
- Spheres are used in science to model planets and celestial bodies.
The properties of spheres, such as their symmetry and curvature, make them useful in a wide range of applications.
Mathematical Properties of Spheres
Spheres have several mathematical properties that make them interesting and useful. Here are some examples:
- Spheres are symmetric about their center.
- Spheres have constant curvature.
- Spheres have a finite volume and surface area.
The mathematical properties of spheres make them a fascinating topic of study in mathematics and geometry.
What is the formula for sphere and volume?
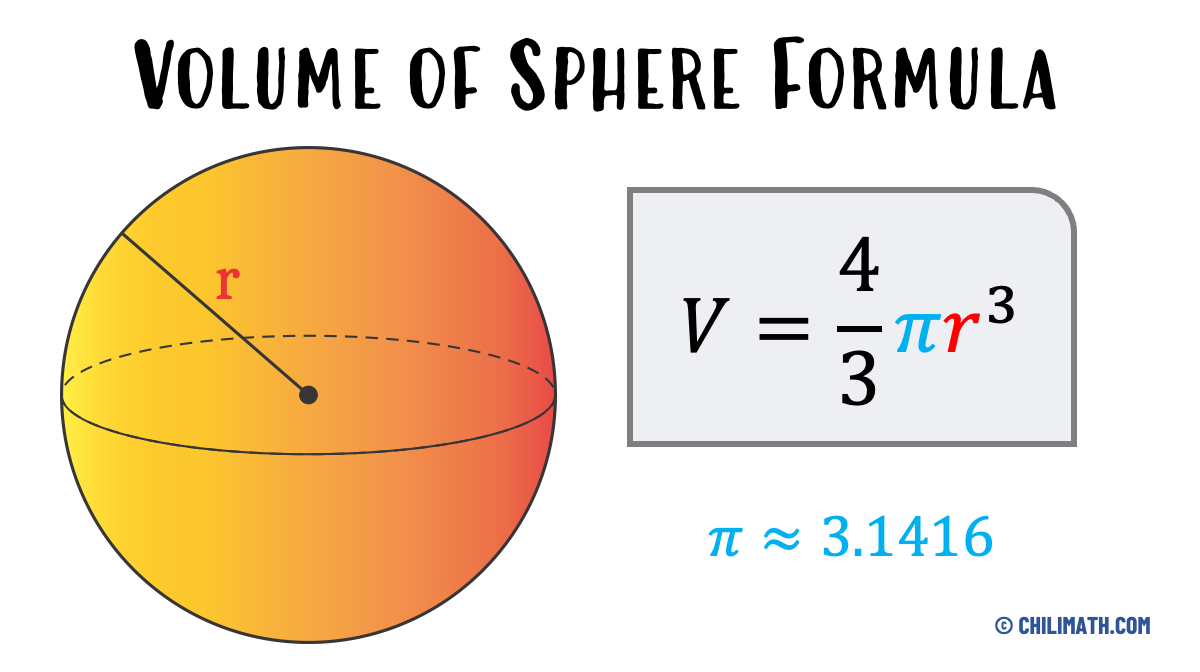
The formula for the volume of a sphere is (4/3)πr³, where r is the radius of the sphere. This formula is derived from the integration of the area of the sphere's cross-sections.
Understanding the Sphere Formula
The formula for the volume of a sphere is based on the principle of integration, where the area of the cross-sections is integrated to find the volume. The formula can be broken down into:
- The radius of the sphere (r) is squared and then cubed to find the volume.
- The constant π (pi) is used to represent the ratio of a circle's circumference to its diameter.
- The fraction 4/3 is used to represent the proportion of the sphere's volume to its surface area.
Calculating the Volume of a Sphere
To calculate the volume of a sphere, you need to know the radius of the sphere. The formula can be applied by:
- Measuring the diameter of the sphere and dividing it by 2 to find the radius.
- Plugging the radius into the formula (4/3)πr³ to find the volume.
- Using a calculator to evaluate the expression and find the volume.
The result will be the volume of the sphere in cubic units.
Sphere Volume Applications
The formula for the volume of a sphere has many practical applications in:
- Engineering, where it is used to design spherical containers and structures.
- Architecture, where it is used to design domes and spherical buildings.
- Physics, where it is used to study the behavior of spherical objects in motion.
These applications rely on the accurate calculation of the sphere's volume.
Derivation of the Sphere Formula
The formula for the volume of a sphere can be derived using:
- Integration, where the area of the cross-sections is integrated to find the volume.
- Geometry, where the properties of spheres and circles are used to derive the formula.
- Calculus, where the limit of the sum of the areas of the cross-sections is used to find the volume.
The derivation of the formula is based on the principles of mathematics and geometry.
Sphere Volume in Different Dimensions
The formula for the volume of a sphere can be extended to:
- Higher dimensions, where the volume of a sphere in n-dimensional space is calculated using the formula (π^(n/2))/(Γ(n/2 + 1))r^n.
- Lower dimensions, where the volume of a sphere in 2-dimensional space is calculated using the formula πr^2.
- Fractional dimensions, where the volume of a sphere in fractional dimensional space is calculated using fractal geometry.
The formula for the volume of a sphere is a fundamental concept in geometry and mathematics, and its applications are diverse and far-reaching.
Why is 4:3 used in the volume of a sphere?

The volume of a sphere is given by the formula (4/3)πr³, where r is the radius of the sphere. This formula is derived from the integration of the area of the sphere's cross-sections. The number 4/3 appears in this formula because it is the result of the integration process, which involves the summation of the areas of the cross-sections. The value of 4/3 is a constant that arises from the geometric properties of the sphere, specifically from the ratio of the sphere's volume to its surface area.
Derivation of the Volume Formula
The derivation of the volume formula involves the use of calculus, specifically the method of disks or washers. This method involves integrating the area of the sphere's cross-sections with respect to the radius. The result of this integration is the formula (4/3)πr³, which gives the volume of the sphere. The steps involved in this derivation are:
- The area of the sphere's cross-section is given by the formula πr², where r is the radius of the sphere.
- The volume of the sphere is given by the integral of the area of the cross-sections with respect to the radius.
- The result of this integration is the formula (4/3)πr³, which gives the volume of the sphere.
Geometric Interpretation of the Volume Formula
The volume formula (4/3)πr³ has a geometric interpretation, which involves the ratio of the sphere's volume to its surface area. The number 4/3 appears in this formula because it is the constant of proportionality between the volume and the surface area of the sphere. The geometric properties of the sphere, such as its symmetry and curvature, are reflected in the value of this constant. The key points to consider are:
- The sphere is a symmetric object, which means that its volume and surface area are related by a simple proportionality constant.
- The curvature of the sphere affects the ratio of its volume to its surface area.
- The value of 4/3 is a universal constant that applies to all spheres, regardless of their size or shape.
Physical Applications of the Volume Formula
The volume formula (4/3)πr³ has many physical applications, such as calculating the volume of spherical objects, like balls or marbles. This formula is also used in engineering and architecture to calculate the volume of spherical structures, like dome-shaped buildings. The steps involved in these calculations are:
- The radius of the sphere is measured or given.
- The volume of the sphere is calculated using the formula (4/3)πr³.
- The result is used to determine the physical properties of the sphere, such as its weight or buoyancy.
Mathematical Properties of the Volume Formula
The volume formula (4/3)πr³ has several mathematical properties, such as being a polynomial function of the radius. This formula can also be differentiated and integrated to obtain other mathematical expressions. The key points to consider are:
- The formula is a polynomial function of the radius, which means that it can be differentiated and integrated using standard techniques.
- The derivative of the formula gives the surface area of the sphere.
- The integral of the formula gives the volume of the sphere.
Historical Development of the Volume Formula
The volume formula (4/3)πr³ has a rich historical development, which involves the contributions of many mathematicians and scientists. The ancient Greeks, such as Archimedes, were among the first to study the properties of spheres and calculate their volumes. The steps involved in this historical development are:
- The ancient Greeks, such as Archimedes, studied the properties of spheres and calculated their volumes using geometric methods.
- The development of calculus in the 17th century allowed for the derivation of the volume formula using analytic methods.
- The formula was later refined and generalized to apply to other types of spheres, such as ellipsoids and tori.
What is the formula for the area of a sphere?

The formula for the area of a sphere is 4πr², where r is the radius of the sphere. This formula is derived from the idea that the surface area of a sphere is equal to the area of a circle multiplied by 4π.
Introduction to Sphere Surface Area
The surface area of a sphere is a fundamental concept in geometry and is used in various applications, including engineering, physics, and computer science. To calculate the surface area of a sphere, we need to know the radius of the sphere. The formula for the surface area of a sphere is 4πr², where r is the radius of the sphere. Some key points about the surface area of a sphere include:
- The surface area of a sphere is proportional to the square of its radius.
- The surface area of a sphere is a smooth and continuous shape.
- The surface area of a sphere can be calculated using the formula 4πr².
Derivation of the Formula
The formula for the area of a sphere can be derived using integral calculus. The idea is to divide the sphere into small triangles and calculate the area of each triangle. The sum of the areas of these triangles gives us the total surface area of the sphere. The formula for the surface area of a sphere is 4πr², where r is the radius of the sphere. Some key steps in deriving the formula include:
- Divide the sphere into small triangles.
- Calculate the area of each triangle using the formula (base × height) / 2.
- Sum up the areas of all the triangles to get the total surface area of the sphere.
Applications of Sphere Surface Area
The surface area of a sphere has many practical applications in various fields, including engineering, physics, and computer science. For example, the surface area of a sphere is used to calculate the drag force on an object moving through a fluid. The formula for the surface area of a sphere is 4πr², where r is the radius of the sphere. Some key applications of sphere surface area include:
- Calculating the drag force on an object moving through a fluid.
- Designing spherical shapes for aerodynamic or hydrodynamic applications.
- Modeling the behavior of particles or objects in a three-dimensional space.
Sphere Surface Area in Real-World Scenarios
The surface area of a sphere is used in many real-world scenarios, including architecture, engineering, and design. For example, the surface area of a sphere is used to calculate the surface area of a dome or a sphere-shaped building. The formula for the surface area of a sphere is 4πr², where r is the radius of the sphere. Some key scenarios where sphere surface area is used include:
- Designing dome-shaped buildings or stadiums.
- Calculating the surface area of a sphere-shaped container or tank.
- Modeling the behavior of particles or objects in a three-dimensional space.
Calculating Sphere Surface Area with Different Units
The surface area of a sphere can be calculated using different units, including meters, feet, or inches. The formula for the surface area of a sphere is 4πr², where r is the radius of the sphere. Some key points to keep in mind when calculating sphere surface area with different units include:
- Make sure to use the correct units for the radius and the surface area.
- Use the conversion factors to convert between different units.
- Be careful when rounding or truncating the results to avoid errors.
Frequently Asked Questions (FAQs)
What is the formula for calculating the volume and area of a sphere?
The formula for calculating the volume of a sphere is ( V = frac{4}{3} pi r^3 ), where ( V ) is the volume and ( r ) is the radius of the sphere. This formula is derived from the integration of the area of circular cross-sections of the sphere. The area of each cross-section is ( A = pi r^2 ), and as you move along the axis of the sphere, the radius of these cross-sections changes. The formula for the surface area of a sphere is ( A = 4 pi r^2 ), which is derived by integrating the area of these cross-sections over the entire sphere. Understanding these formulas is crucial for calculating the volume and area of a sphere using the equation and calculator.
How does the volume and area of a sphere calculator work?
The calculator for the volume and area of a sphere works by taking the radius of the sphere as input and then using the formulas for volume and surface area to calculate the respective values. The user simply needs to enter the radius of the sphere they are interested in, and the calculator will automatically compute the volume using the formula ( V = frac{4}{3} pi r^3 ) and the surface area using the formula ( A = 4 pi r^2 ). The calculator can be a software program, a web-based tool, or even a spreadsheet that has been set up with these formulas. The advantage of using a calculator is that it quickly and accurately performs the calculations, saving time and reducing the chance of errors. Additionally, some calculators may also provide additional features, such as graphing the sphere or calculating other properties.
What are the real-world applications of calculating the volume and area of a sphere?
Calculating the volume and area of a sphere has numerous real-world applications in fields such as engineering, architecture, and physics. For example, in engineering, the volume of a sphere might be used to determine the amount of material needed to manufacture a spherical container or tank. In architecture, the surface area of a sphere might be used to calculate the amount of material needed for a domed roof or the surface area of a spherical sculpture. In physics, the volume and surface area of a sphere are used to calculate physical properties such as buoyancy, moment of inertia, and surface tension. Additionally, spherical shapes are found in nature, such as the earth and other planets, and understanding their volume and surface area is crucial for scientific research and space exploration.
How can I use the volume and area of a sphere equation and calculator for educational purposes?
The equation and calculator for the volume and area of a sphere can be a valuable educational tool for students learning about geometry and mathematics. Teachers can use the calculator to demonstrate how the volume and surface area of a sphere change as the radius increases or decreases, helping students to visualize and understand the concepts. The equation can be used to teach students about the derivation of mathematical formulas and how they are used to model real-world objects. Additionally, students can use the calculator to explore different scenarios and problems, such as calculating the volume of a sphere that can fit inside a cube, or determining the surface area of a sphere that is inscribed within a polyhedron. By using the equation and calculator, students can gain a deeper understanding of mathematical concepts and develop problem-solving skills.
Deja una respuesta

Entradas Relacionadas