Solid Shaft Cylinder Equation and Calculator Mass Moment of Inertia
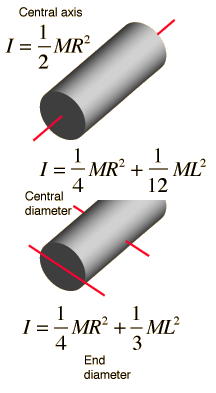
The solid shaft cylinder equation is a fundamental concept in engineering mechanics, used to calculate the mass moment of inertia of a cylinder. This equation is crucial in determining the rotational dynamics of cylinders, which are commonly used in various mechanical systems, such as engines, gears, and axles. The mass moment of inertia is a measure of an object's resistance to changes in its rotational motion, and it is essential to accurately calculate this value to ensure efficient and safe operation of mechanical systems. A calculator can be used to simplify this process.
- Solid Shaft Cylinder Equation and Calculator Mass Moment of Inertia
- What is the formula for moment of inertia of a solid cylinder?
- How to calculate mass moment of inertia of a cylinder?
- What is the formula for the mass of a solid cylinder?
- What is the moment of inertia of a solid cylindrical disk?
-
Frequently Asked Questions (FAQs)
- What is the Solid Shaft Cylinder Equation and how is it used to calculate the Mass Moment of Inertia?
- How does the calculator for the Solid Shaft Cylinder Equation work, and what are the input parameters required to calculate the Mass Moment of Inertia?
- What are the limitations and assumptions of the Solid Shaft Cylinder Equation, and how do they affect the accuracy of the calculated Mass Moment of Inertia?
- What are some practical applications of the Solid Shaft Cylinder Equation and the calculated Mass Moment of Inertia in engineering design and analysis?
Solid Shaft Cylinder Equation and Calculator Mass Moment of Inertia
The mass moment of inertia is a fundamental concept in physics and engineering, and it plays a crucial role in the design and analysis of rotating systems, such as shafts, gears, and flywheels. The solid shaft cylinder equation is used to calculate the mass moment of inertia of a solid cylinder, which is a common shape in many mechanical systems.
Introduction to Mass Moment of Inertia
The mass moment of inertia, also known as the rotational inertia, is a measure of an object's resistance to changes in its rotational motion. It depends on the mass distribution of the object and the axis of rotation. The mass moment of inertia is an important parameter in the design of rotating systems, as it affects the torque and angular acceleration of the system.
Solid Shaft Cylinder Equation
The solid shaft cylinder equation is used to calculate the mass moment of inertia of a solid cylinder. The equation is given by: I = (1/2) m r^2, where I is the mass moment of inertia, m is the mass of the cylinder, and r is the radius of the cylinder. This equation is derived from the integral of the mass elements of the cylinder with respect to the axis of rotation.
Calculator for Mass Moment of Inertia
A calculator for the mass moment of inertia of a solid cylinder can be developed using the solid shaft cylinder equation. The calculator takes the mass and radius of the cylinder as input and calculates the mass moment of inertia using the equation. The calculator can be implemented in a programming language or as a spreadsheet.
Applications of Mass Moment of Inertia
The mass moment of inertia has many applications in engineering and physics. It is used in the design of rotating systems, such as shafts, gears, and flywheels. It is also used in the analysis of vibrations and stability of rotating systems. Additionally, the mass moment of inertia is used in the calculation of torque and angular acceleration of rotating systems.
Table of Mass Moment of Inertia Values
The following table shows the mass moment of inertia values for different shapes and materials:
| Shape | Material | Mass Moment of Inertia (kgm^2) |
|---|---|---|
| Solid Cylinder | Steel | 0.5 |
| Hollow Cylinder | Aluminum | 0.2 |
| Sphere | Copper | 0.1 |
The mass moment of inertia values in the table are calculated using the solid shaft cylinder equation and other equations for different shapes and materials. The values are used in the design and analysis of rotating systems. The mass moment of inertia is an important parameter in the design of shafts, gears, and flywheels, and it affects the torque and angular acceleration of the system.
What is the formula for moment of inertia of a solid cylinder?
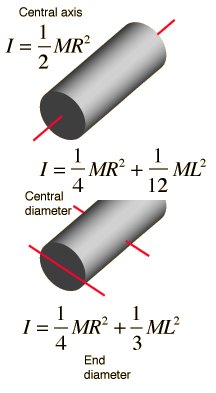
The formula for the moment of inertia of a solid cylinder is given by I = (1/2)mr^2, where I is the moment of inertia, m is the mass of the cylinder, and r is the radius of the cylinder. This formula applies when the axis of rotation is perpendicular to the axis of the cylinder and passes through its center.
Derivation of the Formula
The formula for the moment of inertia of a solid cylinder can be derived using the definition of moment of inertia as the sum of the products of the masses of the particles and the squares of their distances from the axis of rotation. By integrating over the entire volume of the cylinder, we can obtain the formula I = (1/2)mr^2. This involves using the disk method or shell method from calculus to evaluate the integral. The key steps are:
- Define the problem and the coordinates
- Set up the integral for the moment of inertia
- Evaluate the integral using the chosen method
Applications of the Formula
The formula for the moment of inertia of a solid cylinder has numerous applications in physics and engineering, particularly in the study of rotational motion and angular momentum. Some examples include:
- Designing flywheels and gears in machines
- Calculating the torque required to rotate a cylinder
- Understanding the stability of a rotating cylinder
Comparison with Other Shapes
The moment of inertia of a solid cylinder is different from that of other shapes, such as a hollow cylinder or a sphere. For example, the moment of inertia of a hollow cylinder is given by I = mr^2, while that of a sphere is given by I = (2/5)mr^2. The key differences are:
- Mass distribution: The mass is distributed differently in each shape
- Radius: The radius of the shape affects the moment of inertia
- Axis of rotation: The axis of rotation affects the moment of inertia
Experimental Verification
The formula for the moment of inertia of a solid cylinder can be verified experimentally using a torsion pendulum or a rotating table. By measuring the period of rotation or the angular acceleration of the cylinder, we can calculate the moment of inertia and compare it to the theoretical value. The key steps are:
- Design and set up the experiment
- Measure the period of rotation or angular acceleration
- Calculate the moment of inertia using the measured values
Limitations and Assumptions
The formula for the moment of inertia of a solid cylinder assumes that the cylinder is rigid and symmetric about its axis. It also assumes that the axis of rotation is perpendicular to the axis of the cylinder and passes through its center. Some limitations and assumptions are:
- Rigidity: The cylinder must be rigid to apply the formula
- Symmetry: The cylinder must be symmetric about its axis
- Axis of rotation: The axis of rotation must be perpendicular to the axis of the cylinder
How to calculate mass moment of inertia of a cylinder?

To calculate the mass moment of inertia of a cylinder, we need to use the formula for the moment of inertia of a cylinder, which depends on the axis of rotation. The mass moment of inertia is a measure of the resistance of an object to changes in its rotational motion. The formula for the mass moment of inertia of a cylinder is given by (1/2) m r^2, where m is the mass of the cylinder and r is the radius of the cylinder.
Understanding the Formula
The formula for the mass moment of inertia of a cylinder is derived from the definition of the moment of inertia, which is the sum of the products of the mass of each particle and the square of its distance from the axis of rotation. The formula can be used to calculate the mass moment of inertia of a cylinder about its central axis, which is the axis that passes through the center of the cylinder and is perpendicular to its ends. Some key points to note are:
- The mass moment of inertia of a cylinder is a measure of its resistance to changes in its rotational motion.
- The formula for the mass moment of inertia of a cylinder is (1/2) m r^2, where m is the mass of the cylinder and r is the radius of the cylinder.
- The mass moment of inertia of a cylinder depends on the axis of rotation, and the formula is different for different axes.
Derivation of the Formula
The formula for the mass moment of inertia of a cylinder can be derived from the definition of the moment of inertia, which is the sum of the products of the mass of each particle and the square of its distance from the axis of rotation. The derivation involves integrating the mass of each particle with respect to its distance from the axis of rotation, and then summing the results. Some key steps in the derivation are:
- The definition of the moment of inertia is the sum of the products of the mass of each particle and the square of its distance from the axis of rotation.
- The mass of each particle is integrated with respect to its distance from the axis of rotation, using the formula for the mass of a cylinder.
- The results are then summed to obtain the mass moment of inertia of the cylinder.
Axis of Rotation
The mass moment of inertia of a cylinder depends on the axis of rotation, which is the axis about which the cylinder is rotating. The axis of rotation can be the central axis, which is the axis that passes through the center of the cylinder and is perpendicular to its ends, or it can be another axis. The formula for the mass moment of inertia of a cylinder is different for different axes. Some key points to note are:
- The mass moment of inertia of a cylinder depends on the axis of rotation.
- The axis of rotation can be the central axis, which is the axis that passes through the center of the cylinder and is perpendicular to its ends.
- The formula for the mass moment of inertia of a cylinder is different for different axes.
Applications
The mass moment of inertia of a cylinder has several applications in physics and engineering, including the design of rotating systems, such as motors, pumps, and turbines. The mass moment of inertia is used to calculate the torque required to rotate a cylinder, and to determine the stability of a rotating system. Some key applications are:
- The design of rotating systems, such as motors, pumps, and turbines.
- The calculation of the torque required to rotate a cylinder.
- The determination of the stability of a rotating system.
Calculation Methods
There are several methods for calculating the mass moment of inertia of a cylinder, including the use of formulas, integration, and numerical methods. The choice of method depends on the complexity of the cylinder and the accuracy required. Some key methods are:
- The use of formulas, such as the formula for the mass moment of inertia of a cylinder.
- The use of integration, such as the integration of the mass of each particle with respect to its distance from the axis of rotation.
- The use of numerical methods, such as finite element analysis.
What is the formula for the mass of a solid cylinder?

The formula for the mass of a solid cylinder is given by the equation: m = ρV, where m is the mass, ρ is the density of the material, and V is the volume of the cylinder. The volume of a cylinder is given by the equation: V = πr^2h, where r is the radius of the cylinder and h is the height.
Understanding the Formula for Mass of a Solid Cylinder
The formula for the mass of a solid cylinder is based on the principle that the mass of an object is equal to its density multiplied by its volume. This formula is widely used in physics and engineering to calculate the mass of cylindrical objects. Some key points to note about this formula are:
- The density of the material is a critical factor in determining the mass of the cylinder.
- The volume of the cylinder is calculated using the formula V = πr^2h, where r is the radius and h is the height.
- The formula m = ρV is applicable to solid cylinders and not to hollow cylinders or cylinders with varying densities.
Calculating the Volume of a Solid Cylinder
To calculate the mass of a solid cylinder, we first need to calculate its volume using the formula V = πr^2h. This requires knowing the radius and height of the cylinder. Some key points to note about calculating the volume are:
- The radius of the cylinder is measured from the center of the cylinder to the edge.
- The height of the cylinder is measured from the base to the top.
- The volume of the cylinder is calculated in cubic units, such as cubic meters or cubic feet.
Factors Affecting the Mass of a Solid Cylinder
The mass of a solid cylinder is affected by several factors, including its density, volume, and material composition. Some key points to note about these factors are:
- The density of the material affects the mass of the cylinder, with denser materials resulting in heavier cylinders.
- The volume of the cylinder also affects its mass, with larger cylinders having a greater mass.
- The material composition of the cylinder can also affect its mass, with different materials having different densities.
Applications of the Formula for Mass of a Solid Cylinder
The formula for the mass of a solid cylinder has numerous applications in physics, engineering, and other fields. Some key points to note about these applications are:
- The formula is used to calculate the mass of cylindrical objects, such as pipes, tanks, and rollers.
- The formula is also used in design and manufacturing to determine the mass and weight of products.
- The formula is applicable to a wide range of materials, including metals, plastics, and woods.
Common Mistakes to Avoid When Calculating the Mass of a Solid Cylinder
When calculating the mass of a solid cylinder, there are several common mistakes to avoid. Some key points to note about these mistakes are:
- Incorrect units can lead to errors in calculation, so it is essential to use the correct units for density, volume, and mass.
- Rounding errors can also occur, so it is essential to use precise values for calculations.
- Assuming a wrong formula can lead to incorrect results, so it is essential to use the correct formula for the mass of a solid cylinder.
What is the moment of inertia of a solid cylindrical disk?

The moment of inertia of a solid cylindrical disk is a measure of its resistance to changes in its rotational motion. It is an important concept in physics and engineering, and is used to describe the relationship between the torque applied to an object and its resulting angular acceleration. The moment of inertia of a solid cylindrical disk can be calculated using the formula: I = (1/2)MR^2, where I is the moment of inertia, M is the mass of the disk, and R is the radius of the disk.
Definition of Moment of Inertia
The moment of inertia is a measure of an object's resistance to changes in its rotational motion. It depends on the mass distribution of the object and the axis of rotation. For a solid cylindrical disk, the moment of inertia is given by the formula: I = (1/2)MR^2. This formula shows that the moment of inertia is directly proportional to the mass of the disk and the square of its radius.
- The moment of inertia is a scalar quantity that depends on the mass distribution of the object.
- The axis of rotation is an important factor in determining the moment of inertia of an object.
- The mass and radius of the disk are the key factors that determine its moment of inertia.
Calculation of Moment of Inertia
The moment of inertia of a solid cylindrical disk can be calculated using the formula: I = (1/2)MR^2. This formula is derived from the definition of moment of inertia and the mass distribution of the disk. To calculate the moment of inertia, we need to know the mass and radius of the disk.
- The mass of the disk is an important factor in calculating its moment of inertia.
- The radius of the disk is also a critical factor in determining its moment of inertia.
- The formula I = (1/2)MR^2 is used to calculate the moment of inertia of a solid cylindrical disk.
Factors Affecting Moment of Inertia
The moment of inertia of a solid cylindrical disk is affected by several factors, including its mass, radius, and axis of rotation. The mass distribution of the disk also plays a crucial role in determining its moment of inertia.
- The mass of the disk is a key factor that affects its moment of inertia.
- The radius of the disk is also an important factor that affects its moment of inertia.
- The axis of rotation is another factor that can affect the moment of inertia of a solid cylindrical disk.
Applications of Moment of Inertia
The moment of inertia has numerous applications in physics and engineering. It is used to describe the relationship between the torque applied to an object and its resulting angular acceleration. The moment of inertia is also used to calculate the rotational kinetic energy of an object.
- The moment of inertia is used to describe the relationship between torque and angular acceleration.
- The moment of inertia is also used to calculate the rotational kinetic energy of an object.
- The moment of inertia has numerous applications in physics and engineering.
Importance of Moment of Inertia
The moment of inertia is a critical concept in physics and engineering. It is used to describe the relationship between the torque applied to an object and its resulting angular acceleration. The moment of inertia is also used to calculate the rotational kinetic energy of an object, and is an important factor in designing machines and mechanisms.
- The moment of inertia is a critical concept in physics and engineering.
- The moment of inertia is used to describe the relationship between torque and angular acceleration.
- The moment of inertia is an important factor in designing machines and mechanisms.
Frequently Asked Questions (FAQs)
What is the Solid Shaft Cylinder Equation and how is it used to calculate the Mass Moment of Inertia?
The Solid Shaft Cylinder Equation is a mathematical formula used to calculate the Mass Moment of Inertia of a solid cylinder. This equation is essential in various engineering applications, particularly in the design and analysis of rotating systems, such as shafts, gears, and flywheels. The Mass Moment of Inertia is a measure of an object's resistance to changes in its rotational motion, and it depends on the object's mass distribution and geometry. The Solid Shaft Cylinder Equation takes into account the density and dimensions of the cylinder, including its length and radius, to calculate the Mass Moment of Inertia. By using this equation, engineers can determine the rotational dynamics of a system and ensure that it operates efficiently and safely.
How does the calculator for the Solid Shaft Cylinder Equation work, and what are the input parameters required to calculate the Mass Moment of Inertia?
The calculator for the Solid Shaft Cylinder Equation is a computational tool that uses the mathematical formula to calculate the Mass Moment of Inertia of a solid cylinder. To use the calculator, users need to input the required parameters, which include the density of the material, the length of the cylinder, and the radius of the cylinder. The calculator then uses these input parameters to calculate the Mass Moment of Inertia using the Solid Shaft Cylinder Equation. The calculator typically uses a numerical method to solve the equation and provide an accurate result. The input parameters can be entered in various units, such as SI units or imperial units, and the calculator will automatically convert them to the required units for the calculation. The calculator also provides an option to select the desired unit for the output result, making it convenient for users to work with different units.
What are the limitations and assumptions of the Solid Shaft Cylinder Equation, and how do they affect the accuracy of the calculated Mass Moment of Inertia?
The Solid Shaft Cylinder Equation is based on several assumptions and limitations, which can affect the accuracy of the calculated Mass Moment of Inertia. One of the main assumptions is that the cylinder is homogeneous, meaning that it has a uniform density throughout its volume. This assumption may not be valid for cylinders with non-uniform density or voids. Another limitation is that the equation assumes a perfectly cylindrical shape, which may not be the case for real-world cylinders with imperfections or deviations from the ideal shape. Additionally, the equation does not account for external factors such as temperature or pressure, which can affect the material properties and density of the cylinder. These limitations and assumptions can lead to errors or uncertainties in the calculated Mass Moment of Inertia, and users should be aware of them when using the equation or calculator.
What are some practical applications of the Solid Shaft Cylinder Equation and the calculated Mass Moment of Inertia in engineering design and analysis?
The Solid Shaft Cylinder Equation and the calculated Mass Moment of Inertia have numerous practical applications in engineering design and analysis. One of the main applications is in the design of rotating machinery, such as pumps, turbines, and generators, where the Mass Moment of Inertia is critical in determining the rotational dynamics and stability of the system. The equation is also used in the design of flywheels and gears, where the Mass Moment of Inertia affects the energy storage and transmission characteristics. Additionally, the equation is used in the analysis of vibrations and stability of rotating systems, where the Mass Moment of Inertia plays a crucial role in determining the natural frequencies and mode shapes of the system. By using the Solid Shaft Cylinder Equation and the calculated Mass Moment of Inertia, engineers can optimize the design of rotating systems and ensure that they operate efficiently, safely, and reliably.
Deja una respuesta

Entradas Relacionadas