Simple Pendulum Natural Frequency and Period Equations and Calculator
The simple pendulum is a fundamental concept in physics, consisting of a mass attached to a massless string or rod. The natural frequency and period of a simple pendulum are critical parameters that describe its oscillatory motion. These values can be calculated using specific equations that take into account the pendulum's length and the acceleration due to gravity. This article provides a comprehensive overview of the equations and a calculator to determine the natural frequency and period of a simple pendulum, enabling users to understand and predict its behavior under various conditions. Accurate calculations are essential.
-
Understanding Simple Pendulum Natural Frequency and Period Equations and Calculator
- Introduction to Simple Pendulum Natural Frequency and Period Equations
- Derivation of Simple Pendulum Natural Frequency and Period Equations
- Simple Pendulum Natural Frequency and Period Calculator
- Applications of Simple Pendulum Natural Frequency and Period Equations
- Limitations and Assumptions of Simple Pendulum Natural Frequency and Period Equations
- What is the formula of time period and frequency of simple pendulum?
- What is the formula for the period of a pendulum calculator?
-
Frequently Asked Questions (FAQs)
- What is the simple pendulum natural frequency and period equations and calculator?
- How do the natural frequency and period of a simple pendulum depend on its length and gravity?
- What are the assumptions and limitations of the simple pendulum natural frequency and period equations and calculator?
- How can the simple pendulum natural frequency and period equations and calculator be applied in real-world scenarios?
Understanding Simple Pendulum Natural Frequency and Period Equations and Calculator
The simple pendulum is a fundamental concept in physics, and its natural frequency and period are crucial in understanding its behavior. The natural frequency of a simple pendulum is the frequency at which it oscillates when displaced from its equilibrium position and released. The period of a simple pendulum is the time taken for one complete oscillation. The equations that govern the natural frequency and period of a simple pendulum are based on its physical parameters, such as the length of the pendulum and the acceleration due to gravity.
Introduction to Simple Pendulum Natural Frequency and Period Equations
The natural frequency (f) of a simple pendulum is given by the equation f = (1/2π) √(g/L), where g is the acceleration due to gravity and L is the length of the pendulum. The period (T) of a simple pendulum is given by the equation T = 2π √(L/g). These equations are derived from the physics of the pendulum's motion and are used to calculate the natural frequency and period of the pendulum.
Derivation of Simple Pendulum Natural Frequency and Period Equations
The derivation of the natural frequency and period equations involves the application of Newton's laws of motion and the equations of motion for a simple pendulum. The pendulum's motion is modeled as a simple harmonic motion, and the equations are derived from the differential equation that governs this motion. The resulting equations provide a mathematical model of the pendulum's behavior and can be used to calculate its natural frequency and period.
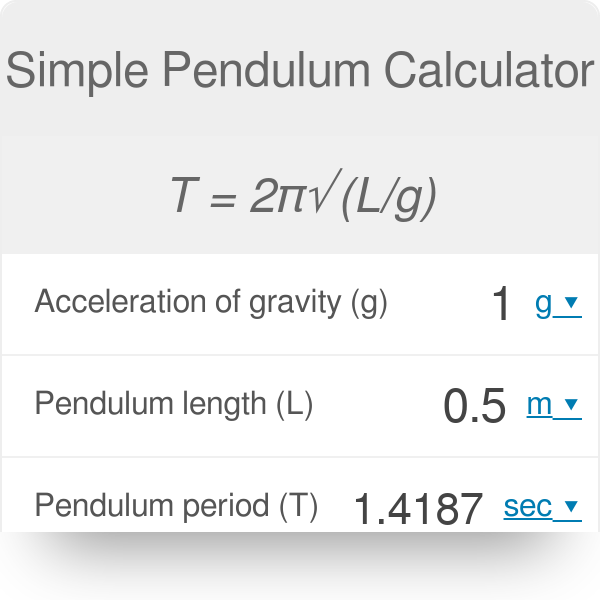
Simple Pendulum Natural Frequency and Period Calculator
A calculator can be used to calculate the natural frequency and period of a simple pendulum using the equations mentioned earlier. The calculator takes the length of the pendulum and the acceleration due to gravity as input and calculates the natural frequency and period. The calculator can be implemented using a computer program or a spreadsheet, and it provides a quick and easy way to calculate the natural frequency and period of a simple pendulum.
Applications of Simple Pendulum Natural Frequency and Period Equations
The natural frequency and period equations of a simple pendulum have many applications in physics and engineering. They are used to design and analyze pendulum-based systems, such as clocks and seismometers. They are also used to study the behavior of complex systems, such as coupled pendulums. The equations provide a fundamental understanding of the physics of pendulums and are essential for designing and optimizing pendulum-based systems.
Limitations and Assumptions of Simple Pendulum Natural Frequency and Period Equations
The natural frequency and period equations of a simple pendulum are based on simplifying assumptions, such as a rigid pendulum and a constant gravitational field. They do not take into account real-world effects, such as air resistance and pendulum flexibility. The equations are also limited to small angles of oscillation, and they do not apply to large angles or nonlinear pendulum motion. The limitations and assumptions of the equations must be considered when applying them to real-world problems.
| Parameter | Symbol | Units |
|---|---|---|
| Natural Frequency | f | Hz |
| Period | T | s |
| Length | L | m |
| Acceleration due to Gravity | g | m/s^2 |
What is the formula of time period and frequency of simple pendulum?

The formula for the time period and frequency of a simple pendulum is given by the following equations:
T = 2π √(L/g) and f = 1/T = 1/(2π √(L/g)), where T is the time period, f is the frequency, L is the length of the pendulum, and g is the acceleration due to gravity.
Time Period of Simple Pendulum
The time period of a simple pendulum is the time taken by the pendulum to complete one oscillation. The time period is given by the formula T = 2π √(L/g). The factors that affect the time period of a simple pendulum are:
- The length of the pendulum: The time period is directly proportional to the square root of the length of the pendulum.
- The acceleration due to gravity: The time period is inversely proportional to the square root of the acceleration due to gravity.
- The amplitude of oscillation: The time period is independent of the amplitude of oscillation, as long as the amplitude is small.
Frequency of Simple Pendulum
The frequency of a simple pendulum is the number of oscillations per unit time. The frequency is given by the formula f = 1/T = 1/(2π √(L/g)). The factors that affect the frequency of a simple pendulum are:
- The length of the pendulum: The frequency is inversely proportional to the square root of the length of the pendulum.
- The acceleration due to gravity: The frequency is directly proportional to the square root of the acceleration due to gravity.
- The amplitude of oscillation: The frequency is independent of the amplitude of oscillation, as long as the amplitude is small.
Derivation of Time Period Formula
The formula for the time period of a simple pendulum can be derived using the equations of motion. The equation of motion for a simple pendulum is given by d^2θ/dt^2 + (g/L) sin(θ) = 0, where θ is the angular displacement of the pendulum. For small amplitudes, the equation of motion can be approximated as d^2θ/dt^2 + (g/L) θ = 0. The solution to this equation is θ(t) = A cos(ωt + φ), where A is the amplitude, ω is the angular frequency, and φ is the phase angle. The time period is given by T = 2π/ω, where ω = √(g/L).
Factors Affecting Time Period and Frequency
The factors that affect the time period and frequency of a simple pendulum are:
- The length of the pendulum: The time period is directly proportional to the square root of the length of the pendulum, while the frequency is inversely proportional to the square root of the length of the pendulum.
- The acceleration due to gravity: The time period is inversely proportional to the square root of the acceleration due to gravity, while the frequency is directly proportional to the square root of the acceleration due to gravity.
- The amplitude of oscillation: The time period and frequency are independent of the amplitude of oscillation, as long as the amplitude is small.
Applications of Simple Pendulum
The simple pendulum has several applications in physics and engineering, including:
- Timekeeping: The simple pendulum is used in clocks to regulate the time.
- Seismology: The simple pendulum is used to measure the magnitude of earthquakes.
- Engineering: The simple pendulum is used to test the stability of structures and to design vibration-resistant systems.
What is the formula for the period of a pendulum calculator?

The formula for the period of a pendulum calculator is given by T = 2π √(L/g), where T is the period of the pendulum, L is the length of the pendulum, and g is the acceleration due to gravity. This formula is derived from the simple harmonic motion of the pendulum and is widely used to calculate the period of a pendulum in various applications.
Understanding the Variables
The variables involved in the formula are length (L), acceleration due to gravity (g), and period (T). To calculate the period of a pendulum, it is essential to understand the values of these variables. The length of the pendulum is the distance from the point of suspension to the center of the pendulum bob, while the acceleration due to gravity is a constant value of approximately 9.81 m/s². The period of the pendulum is the time taken for one complete oscillation.
- The length of the pendulum is measured in meters (m).
- The acceleration due to gravity is measured in meters per second squared (m/s²).
- The period of the pendulum is measured in seconds (s).
Derivation of the Formula
The formula for the period of a pendulum is derived from the equations of motion for a simple pendulum. The pendulum is assumed to be a point mass attached to a massless string, and the motion is restricted to small angles. The angular displacement of the pendulum is related to the angular velocity and angular acceleration through the equations of motion. By solving these equations, the formula for the period of the pendulum can be derived.
- The pendulum is assumed to be a simple pendulum with a point mass attached to a massless string.
- The motion is restricted to small angles, typically less than 10°.
- The equations of motion are solved to derive the formula for the period of the pendulum.
Applications of the Formula
The formula for the period of a pendulum has various practical applications in physics and engineering. It is used to calculate the period of a pendulum in clocks, seismometers, and gravimeters. The formula is also used to study the behavior of pendulums in different environments, such as in space or on other planets.
- The formula is used to calculate the period of a pendulum in clocks and time-keeping devices.
- The formula is used to study the behavior of pendulums in different environments, such as in space or on other planets.
- The formula is used in the design of seismometers and gravimeters to measure seismic activity and gravitational fields.
Limitations of the Formula
The formula for the period of a pendulum has certain limitations and assumptions. It assumes that the pendulum is a simple pendulum with a point mass attached to a massless string, and the motion is restricted to small angles. The formula also assumes that the air resistance and friction are negligible. In reality, these assumptions may not always be valid, and the formula may need to be modified or corrected to account for these factors.
- The formula assumes that the pendulum is a simple pendulum with a point mass attached to a massless string.
- The formula assumes that the motion is restricted to small angles, typically less than 10°.
- The formula assumes that the air resistance and friction are negligible, but in reality, these factors can affect the motion of the pendulum.
Experimental Verification
The formula for the period of a pendulum can be experimentally verified using a simple pendulum apparatus. The length of the pendulum can be varied, and the period of the pendulum can be measured using a timer or oscilloscope. The results can be compared with the theoretical values calculated using the formula to verify its accuracy.
- The length of the pendulum can be varied to measure the effect on the period.
- The period of the pendulum can be measured using a timer or oscilloscope.
- The results can be compared with the theoretical values calculated using the formula to verify its accuracy and validate the assumptions.
Frequently Asked Questions (FAQs)
What is the simple pendulum natural frequency and period equations and calculator?
The simple pendulum is a classic example of a harmonic oscillator, consisting of a mass attached to a massless string of length L. The natural frequency and period of a simple pendulum can be calculated using the following equations: ω = √(g/L) and T = 2π √(L/g), where ω is the angular frequency, T is the period, g is the acceleration due to gravity, and L is the length of the pendulum. The calculator is a tool that allows users to input the values of L and g to calculate the natural frequency and period of the pendulum. This is useful for physics students and engineers who need to design and analyze pendulum-based systems.
How do the natural frequency and period of a simple pendulum depend on its length and gravity?
The natural frequency of a simple pendulum is inversely proportional to the square root of its length L, meaning that as the length of the pendulum increases, its natural frequency decreases. On the other hand, the period of the pendulum is directly proportional to the square root of its length L, meaning that as the length of the pendulum increases, its period also increases. The acceleration due to gravity g also plays a crucial role in determining the natural frequency and period of the pendulum. The natural frequency is directly proportional to the square root of g, while the period is inversely proportional to the square root of g. This means that if the gravity is stronger, the pendulum will oscillate faster and have a shorter period.
What are the assumptions and limitations of the simple pendulum natural frequency and period equations and calculator?
The simple pendulum natural frequency and period equations are based on several assumptions, including that the pendulum is a point mass attached to a massless string, and that the string is inextensible and rigid. Additionally, the equations assume that the pendulum is subject only to the force of gravity and that there is no air resistance or other damping forces. The calculator also assumes that the user inputs the correct values for L and g, and that the pendulum is in a vacuum. In reality, air resistance and other damping forces can affect the motion of the pendulum, causing its period to decrease over time. Furthermore, the string may not be perfectly inextensible or rigid, which can also affect the accuracy of the equations and calculator.
How can the simple pendulum natural frequency and period equations and calculator be applied in real-world scenarios?
The simple pendulum natural frequency and period equations and calculator have numerous real-world applications, including seismology, engineering, and physics research. For example, seismologists use pendulums to measure the ground motion caused by earthquakes, and the natural frequency and period of the pendulum can be used to estimate the magnitude of the earthquake. Engineers also use pendulums in the design of buildings and bridges, where the natural frequency of the structure must be taken into account to ensure that it can withstand external forces such as wind and earthquakes. Additionally, physics researchers use pendulums to study the properties of matter and energy, and the natural frequency and period of the pendulum can be used to measure the gravitational constant and other fundamental constants.
Deja una respuesta

Entradas Relacionadas