Simple Pendulum Natural Frequency and Period Calculator
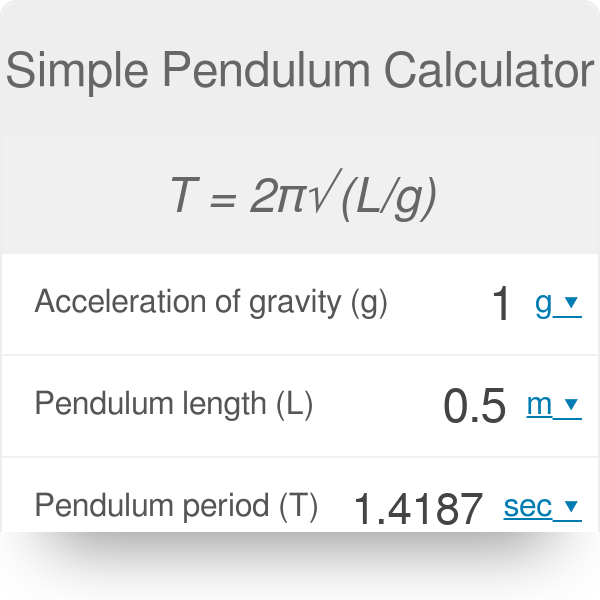
The simple pendulum is a fundamental concept in physics, and understanding its natural frequency and period is crucial in various engineering and scientific applications. The natural frequency and period of a simple pendulum depend on its length and the acceleration due to gravity. This calculator is designed to compute the natural frequency and period of a simple pendulum, given its length and the gravitational acceleration. It uses the mathematical equations that govern the motion of a simple pendulum to provide accurate calculations, making it a useful tool for students, engineers, and researchers. Accurate calculations are provided instantly.
- Understanding the Simple Pendulum Natural Frequency and Period Calculator
- What is the determination of time period and natural frequency of a simple pendulum?
- How to calculate period in simple pendulum?
-
Frequently Asked Questions (FAQs)
- What is the Simple Pendulum Natural Frequency and Period Calculator and how does it work?
- What are the key factors that affect the natural frequency and period of a simple pendulum?
- How can I use the Simple Pendulum Natural Frequency and Period Calculator to design a pendulum clock?
- What are the limitations and assumptions of the Simple Pendulum Natural Frequency and Period Calculator?
Understanding the Simple Pendulum Natural Frequency and Period Calculator
The Simple Pendulum Natural Frequency and Period Calculator is a tool used to calculate the natural frequency and period of a simple pendulum. A simple pendulum is a pendulum that consists of a mass attached to a massless string of length L. The calculator uses the equation for the natural frequency of a simple pendulum, which is given by the formula: f = (1/2π) √(g/L), where f is the natural frequency, g is the acceleration due to gravity, and L is the length of the pendulum.
Introduction to Simple Pendulum Dynamics
Simple pendulum dynamics is the study of the motion of a simple pendulum. The pendulum's motion is periodic, meaning it repeats at regular intervals. The period of the pendulum is the time it takes for the pendulum to complete one cycle of its motion. The natural frequency of the pendulum is related to its period by the equation: f = 1/T, where T is the period.
Calculation of Natural Frequency
The natural frequency of a simple pendulum can be calculated using the formula: f = (1/2π) √(g/L). This formula shows that the natural frequency of the pendulum depends on the length of the pendulum and the acceleration due to gravity. The formula can be rearranged to solve for the length of the pendulum: L = g / (4π²f²).
Calculation of Period
The period of a simple pendulum can be calculated using the formula: T = 2π √(L/g). This formula shows that the period of the pendulum depends on the length of the pendulum and the acceleration due to gravity. The formula can be rearranged to solve for the length of the pendulum: L = g T² / (4π²).
Applications of Simple Pendulum Natural Frequency and Period Calculator
The Simple Pendulum Natural Frequency and Period Calculator has several applications in physics and engineering. It can be used to design and optimize pendulum-based systems, such as clocks and seismometers. It can also be used to study the dynamics of simple pendulums and to understand the principles of periodic motion.
Limitations of Simple Pendulum Natural Frequency and Period Calculator
The Simple Pendulum Natural Frequency and Period Calculator has several limitations. It assumes that the pendulum is a simple pendulum, which means that it consists of a mass attached to a massless string. It also assumes that the acceleration due to gravity is constant, which may not be true in all environments. Additionally, the calculator does not take into account damping or friction, which can affect the motion of the pendulum.
| Variable | Unit | Description |
|---|---|---|
| f | Hz | Natural Frequency |
| T | s | Period |
| g | m/s² | Acceleration due to Gravity |
| L | m | Length of the Pendulum |
What is the determination of time period and natural frequency of a simple pendulum?

The determination of the time period and natural frequency of a simple pendulum is a fundamental concept in physics. A simple pendulum consists of a mass attached to a massless string of length L, and its motion is governed by the equations of motion. The time period (T) is the time taken by the pendulum to complete one oscillation, and the natural frequency (f) is the number of oscillations per unit time.
Introduction to Simple Pendulum
The simple pendulum is a classic example of a harmonic oscillator, where the restoring force is proportional to the displacement. The time period of a simple pendulum is given by the equation T = 2π √(L/g), where L is the length of the pendulum and g is the acceleration due to gravity. The natural frequency is related to the time period by the equation f = 1/T. Some key points to consider are:
- The length of the pendulum affects the time period and natural frequency.
- The mass of the pendulum does not affect the time period or natural frequency.
- The angle of displacement affects the amplitude of the oscillation.
Derivation of Time Period Equation
The time period equation for a simple pendulum can be derived using the equations of motion. The net force acting on the pendulum is given by the equation F = -mg sin(θ), where θ is the angle of displacement. The equation of motion for the pendulum is given by the differential equation d^2θ/dt^2 + (g/L) sin(θ) = 0. For small angles, the sin(θ) term can be approximated as θ, and the equation becomes d^2θ/dt^2 + (g/L) θ = 0. Some key points to consider are:
- The acceleration due to gravity affects the time period.
- The length of the pendulum affects the natural frequency.
- The angle of displacement affects the amplitude of the oscillation.
Factors Affecting Time Period and Natural Frequency
The time period and natural frequency of a simple pendulum are affected by several factors, including the length of the pendulum, the acceleration due to gravity, and the angle of displacement. The mass of the pendulum does not affect the time period or natural frequency. Some key points to consider are:
- The length of the pendulum affects the time period and natural frequency.
- The acceleration due to gravity affects the time period and natural frequency.
- The angle of displacement affects the amplitude of the oscillation.
Experimental Determination of Time Period and Natural Frequency
The time period and natural frequency of a simple pendulum can be determined experimentally using a stopwatch and a ruler. The time period can be measured by timing the oscillations of the pendulum, and the natural frequency can be calculated using the equation f = 1/T. Some key points to consider are:
- The length of the pendulum must be measured accurately.
- The oscillations must be timed accurately.
- The angle of displacement affects the amplitude of the oscillation.
Applications of Simple Pendulum
The simple pendulum has several applications, including clocks, seismometers, and gravimeters. The time period and natural frequency of a simple pendulum are used to measure the acceleration due to gravity, which is essential for geophysical and engineering applications. Some key points to consider are:
- The simple pendulum is used in clocks to measure time.
- The simple pendulum is used in seismometers to measure earthquakes.
- The simple pendulum is used in gravimeters to measure the acceleration due to gravity.
How to calculate period in simple pendulum?

To calculate the period in a simple pendulum, we use the formula: T = 2π √(L/g), where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity. This formula is derived from the equations of motion for a simple pendulum, which assume a frictionless environment and a small amplitude of motion. The period of a simple pendulum is the time it takes for the pendulum to complete one full cycle of motion.
Understanding the Simple Pendulum Formula
The formula for the period of a simple pendulum is based on the physical properties of the pendulum, including its length and the acceleration due to gravity. To calculate the period, we need to know these values. Here are the steps to follow:
- Measure the length of the pendulum from its pivot point to the center of its bob.
- Use the accepted value of the acceleration due to gravity, which is approximately 9.81 m/s² on Earth.
- Plug these values into the formula: T = 2π √(L/g), and calculate the period.
Factors Affecting the Period of a Simple Pendulum
The period of a simple pendulum is affected by several factors, including its length, the acceleration due to gravity, and air resistance. The length of the pendulum has a direct impact on its period, with longer pendulums having longer periods. Here are some key factors to consider:
- The length of the pendulum is the most important factor in determining its period.
- The acceleration due to gravity also affects the period, but it is generally constant on Earth.
- Air resistance can affect the period of a simple pendulum, especially at high speeds or with very light pendulums.
Derivation of the Simple Pendulum Formula
The formula for the period of a simple pendulum is derived from the equations of motion for a pendulum. These equations describe the motion of the pendulum in terms of its angular displacement, angular velocity, and angular acceleration. Here are the key steps in deriving the formula:
- Start with the equation of motion for a pendulum: θ''(t) + (g/L) sin(θ(t)) = 0.
- Use the small angle approximation to simplify the equation: θ''(t) + (g/L) θ(t) = 0.
- Solve the equation using techniques from differential equations, to obtain the formula: T = 2π √(L/g).
Experimental Verification of the Simple Pendulum Formula
The simple pendulum formula can be verified experimentally by measuring the period of a pendulum and comparing it to the theoretical value. This can be done using a stopwatch or timer to measure the time it takes for the pendulum to complete several cycles. Here are the steps to follow:
- Measure the length of the pendulum and calculate its theoretical period using the formula: T = 2π √(L/g).
- Measure the experimental period of the pendulum using a stopwatch or timer.
- Compare the experimental period to the theoretical period to verify the accuracy of the formula.
Applications of the Simple Pendulum Formula
The simple pendulum formula has several practical applications, including the design of clocks, seismometers, and gravimeters. These devices rely on the stable period of a pendulum to measure time or detect gravity. Here are some key applications:
- Clocks: The simple pendulum is used in some clocks to regulate their timekeeping.
- Seismometers: The simple pendulum is used in some seismometers to detect earthquakes and measure seismic activity.
- Gravimeters: The simple pendulum is used in some gravimeters to measure the strength of the gravitational field.
Frequently Asked Questions (FAQs)
What is the Simple Pendulum Natural Frequency and Period Calculator and how does it work?
The Simple Pendulum Natural Frequency and Period Calculator is an online tool designed to calculate the natural frequency and period of a simple pendulum. A simple pendulum is a physical system that consists of a mass attached to a massless string of length L. The calculator uses the mathematical formulas that govern the motion of a simple pendulum to calculate its natural frequency and period. The natural frequency is the number of oscillations per unit time that the pendulum makes when it is displaced from its equilibrium position and released. The period is the time taken by the pendulum to complete one oscillation. The calculator takes the length of the pendulum and the acceleration due to gravity as inputs and calculates the natural frequency and period using the formulas: f = (1/2π) √(g/L) and T = 2π √(L/g), where f is the natural frequency, T is the period, g is the acceleration due to gravity, and L is the length of the pendulum.
What are the key factors that affect the natural frequency and period of a simple pendulum?
The key factors that affect the natural frequency and period of a simple pendulum are the length of the pendulum and the acceleration due to gravity. The length of the pendulum is the most critical factor as it directly affects the natural frequency and period. A longer pendulum has a lower natural frequency and a longer period, while a shorter pendulum has a higher natural frequency and a shorter period. The acceleration due to gravity also plays a significant role as it affects the restoring force that acts on the pendulum. The restoring force is the force that acts on the pendulum to bring it back to its equilibrium position. The acceleration due to gravity is constant on the surface of the Earth, but it can vary slightly depending on the location and altitude. Other factors such as air resistance and friction can also affect the natural frequency and period of a simple pendulum, but they are negligible in most cases.
How can I use the Simple Pendulum Natural Frequency and Period Calculator to design a pendulum clock?
The Simple Pendulum Natural Frequency and Period Calculator can be used to design a pendulum clock by calculating the natural frequency and period of the pendulum. A pendulum clock uses a pendulum to regulate the timekeeping mechanism. The pendulum is designed to swing at a precise frequency, which is used to drive the clock's gears. To design a pendulum clock, you need to calculate the length of the pendulum required to achieve a specific natural frequency. The calculator can be used to calculate the length of the pendulum by inputting the desired natural frequency and the acceleration due to gravity. The calculator will then calculate the length of the pendulum using the formula: L = g / (4 π^2 f^2), where L is the length of the pendulum, g is the acceleration due to gravity, and f is the desired natural frequency. By using the calculator, you can design a pendulum clock with a high degree of accuracy.
What are the limitations and assumptions of the Simple Pendulum Natural Frequency and Period Calculator?
The Simple Pendulum Natural Frequency and Period Calculator is based on the assumption that the pendulum is a simple pendulum, which means that it is a point mass attached to a massless string. The calculator also assumes that the pendulum is subject to a constant acceleration due to gravity and that air resistance and friction are negligible. The calculator uses the small angle approximation, which assumes that the angle of swing is small. This approximation is valid for most practical purposes, but it may not be accurate for very large angles. The calculator also assumes that the pendulum is undamped, which means that it does not lose energy due to friction or air resistance. In real-world applications, the pendulum may be subject to damping, which can affect its natural frequency and period. Additionally, the calculator does not take into account the effects of gravity on the pendulum's motion, such as the variation in gravity with altitude or latitude. Despite these limitations, the calculator is a useful tool for calculating the natural frequency and period of a simple pendulum.
Deja una respuesta

Entradas Relacionadas