Planetary Epicyclic Gear Ratios Equations and Calculators
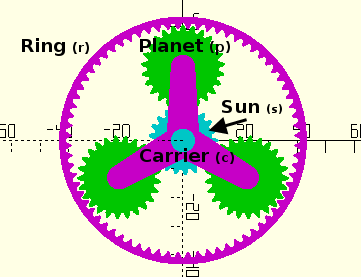
Planetary epicyclic gear ratios are crucial in determining the performance and efficiency of gear systems. These ratios are calculated using complex equations that take into account various factors, including the number of teeth on each gear, the gear configuration, and the desired output speed. Calculators can simplify this process, providing quick and accurate results. In this article, we will explore the equations and calculators used to determine planetary epicyclic gear ratios, and discuss their applications in various fields, including robotics, automotive, and aerospace engineering, to help designers and engineers optimize their gear systems. Key concepts will be explained.
- Understanding Planetary Epicyclic Gear Ratios Equations and Calculators
- How to calculate epicyclic gear ratio?
- What is the formula for the gear ratio of a planetary gear?
- What is the planetary gearbox theory?
-
Frequently Asked Questions (FAQs)
- What are Planetary Epicyclic Gear Ratios and their importance in engineering applications?
- How do you calculate the gear ratios for a planetary epicyclic gear system using equations and calculators?
- What are the advantages and disadvantages of using planetary epicyclic gear ratios in engineering applications?
- How do you design and optimize planetary epicyclic gear ratios for specific engineering applications using calculators and software?
Understanding Planetary Epicyclic Gear Ratios Equations and Calculators
Planetary epicyclic gear ratios equations and calculators are essential tools in the design and analysis of planetary gear systems. These systems are widely used in various applications, including aerospace, automotive, and industrial machinery, due to their high power density, compact design, and flexibility. The equations and calculators used in planetary epicyclic gear systems enable engineers to determine the optimal gear ratios, tooth numbers, and other parameters to achieve the desired performance, efficiency, and reliability.
Introduction to Planetary Epicyclic Gear Systems
Planetary epicyclic gear systems consist of a sun gear, planet gears, and an annulus or ring gear. The planet gears rotate around the sun gear, while the annulus or ring gear surrounds the planet gears. This configuration allows for a high degree of flexibility in designing gear ratios and achieving specific performance characteristics. The planetary gear ratio is calculated using the number of teeth on the sun gear, planet gears, and annulus or ring gear.
Planetary Epicyclic Gear Ratio Equations
The planetary epicyclic gear ratio equations are used to calculate the gear ratio and other parameters. The gear ratio is defined as the ratio of the output speed to the input speed. The equations take into account the number of teeth on each gear, the pitch diameter, and the module. The most common equation used to calculate the planetary epicyclic gear ratio is:
i = (N_s N_p) / (N_s + N_p)
where i is the gear ratio, N_s is the number of teeth on the sun gear, and N_p is the number of teeth on the planet gear.
Planetary Epicyclic Gear Calculators
Planetary epicyclic gear calculators are software tools or online applications that simplify the process of designing and analyzing planetary gear systems. These calculators use the equations and algorithms to calculate the gear ratio, tooth numbers, and other parameters. They also provide a graphical interface to visualize the gear system and analyze its performance. Some common features of planetary epicyclic gear calculators include:
Calculation of gear ratio and tooth numbers
Analysis of gear system performance and efficiency
Visualization of gear system configuration
Optimization of gear system design
| Parameter | Description |
|---|---|
| Sun Gear Teeth | Number of teeth on the sun gear |
| Planet Gear Teeth | Number of teeth on the planet gear |
| Annulus Teeth | Number of teeth on the annulus or ring gear!> |
| Gear Ratio | Ratio of output speed to input speed |
| Pitch Diameter | Diameter of the gear pitch circle |
Applications of Planetary Epicyclic Gear Systems
Planetary epicyclic gear systems have a wide range of applications in various industries, including:
Aerospace: Planetary gear systems are used in aircraft and spacecraft applications due to their high power density and compact design.
Automotive: Planetary gear systems are used in automotive transmissions and drivetrain systems to achieve high efficiency and performance.
Industrial Machinery: Planetary gear systems are used in industrial machinery, such as wind turbines and pumps, to achieve high reliability and efficiency.
Design Considerations for Planetary Epicyclic Gear Systems
When designing planetary epicyclic gear systems, several factors must be considered, including:
Load capacity: The gear system must be designed to withstand the loads and stresses imposed by the application.
Efficiency: The gear system must be designed to achieve high efficiency and minimize energy losses.
Reliability: The gear system must be designed to achieve high reliability and minimize downtime.
Maintenance: The gear system must be designed to be maintainable and minimize maintenance costs.
Future Developments in Planetary Epicyclic Gear Systems
The development of planetary epicyclic gear systems is ongoing, with research focused on improving their performance, efficiency, and reliability. Some areas of research include:
Advanced materials: The use of advanced materials, such as composites and nanomaterials, to improve gear system performance and efficiency.
Optimization techniques: The development of optimization techniques, such as genetic algorithms and finite element analysis, to optimize gear system design and performance.
Condition monitoring: The development of condition monitoring systems to detect faults and anomalies in gear systems and minimize downtime.
How to calculate epicyclic gear ratio?

To calculate the epicyclic gear ratio, it's essential to understand the basic components of an epicyclic gear system, which typically consists of a sun gear, planet gears, and a ring gear. The gear ratio is calculated based on the number of teeth on each gear and the configuration of the system. The formula for calculating the gear ratio in an epicyclic gear system is more complex than in a simple gear system, as it involves the rotation of the planet gears around the sun gear and the ring gear.
Understanding Epicyclic Gear System Components
The calculation of the epicyclic gear ratio starts with understanding the components involved: the sun gear, planet gears, and ring gear. Each of these components plays a crucial role in determining the overall gear ratio. The sun gear is the central gear, the planet gears rotate around the sun gear, and the ring gear is the outer gear that encloses the planet gears. The ratios can be calculated based on the number of teeth on each gear and the configuration of the system.
- Identify the number of teeth on the sun gear, planet gears, and ring gear.
- Determine the configuration of the epicyclic gear system, including how the gears are connected and which gears are fixed or rotating.
- Apply the appropriate formula for calculating the gear ratio based on the system's configuration.
Calculating Gear Ratios in Different Configurations
The gear ratio in an epicyclic gear system can be calculated differently depending on the configuration of the system, such as when the ring gear is fixed, the sun gear is fixed, or when there's a combination of fixed and rotating components. For example, when the ring gear is fixed, the gear ratio is calculated based on the rotation of the sun gear relative to the ring gear. Understanding these different configurations is crucial for accurate calculation.
- Determine the fixed component in the system, which could be the sun gear, ring gear, or the carrier that holds the planet gears.
- Calculate the gear ratio based on the rotation of the input component relative to the output component.
- Consider the direction of rotation and how it affects the gear ratio calculation.
Applying the Formula for Epicyclic Gear Ratio
The formula for the epicyclic gear ratio involves the number of teeth on the sun gear and the ring gear, as well as the configuration of the system. The general formula is ( frac{text{Number of teeth on the ring gear}}{text{Number of teeth on the sun gear}} ), but this can vary depending on the specific configuration and whether the planet gears are involved in the calculation. It's also important to consider the mechanical advantage provided by the epicyclic gear system.
- Apply the basic formula for the gear ratio, considering the number of teeth on the sun gear and ring gear.
- Adjust the formula based on the system's configuration, including the role of the planet gears and any fixed components.
- Consider the effect of the gear ratio on the mechanical advantage and torque output of the system.
Considering the Role of Planet Gears
Planet gears play a significant role in the calculation of the epicyclic gear ratio, as they rotate around the sun gear and interact with the ring gear. The number of planet gears and their teeth count can affect the overall gear ratio and the mechanical advantage of the system. Understanding how the planet gears contribute to the system's operation is crucial for accurate calculations.
- Determine the number of planet gears and their teeth count.
- Calculate the gear ratio considering the interaction between the planet gears, sun gear, and ring gear.
- Analyze how the planet gears affect the mechanical advantage and efficiency of the system.
Accounting for Efficiency and Mechanical Advantage
The efficiency and mechanical advantage of the epicyclic gear system are important considerations when calculating the gear ratio. The mechanical advantage provided by the system can affect the torque and speed output, while efficiency considerations can impact the system's overall performance and energy loss. Understanding these factors is essential for designing and optimizing epicyclic gear systems.
- Calculate the mechanical advantage of the system based on the gear ratio and configuration.
- Consider the efficiency of the system, including any energy losses due to friction or other factors.
- Optimize the gear ratio and system configuration to achieve the desired mechanical advantage and efficiency.
What is the formula for the gear ratio of a planetary gear?

The formula for the gear ratio of a planetary gear is a complex one, involving the number of teeth on the sun gear, the planet gears, and the ring gear. The gear ratio is calculated as the ratio of the output speed to the input speed, and it can be expressed as a function of the number of teeth on each gear. The formula is: (R + S) / S, where R is the number of teeth on the ring gear and S is the number of teeth on the sun gear.
Understanding the Components of a Planetary Gear
To calculate the gear ratio of a planetary gear, it's essential to understand the components involved. The sun gear is the central gear, the planet gears are the gears that orbit around the sun gear, and the ring gear is the outer gear that surrounds the planet gears. The gear ratio is determined by the interaction between these components.
- The planet gears play a crucial role in determining the gear ratio, as they transmit power between the sun gear and the ring gear.
- The gear ratio can be adjusted by changing the number of teeth on the sun gear or the ring gear.
Calculating the Gear Ratio
Calculating the gear ratio of a planetary gear involves using the formula: (R + S) / S. This formula takes into account the number of teeth on the ring gear (R) and the sun gear (S). By plugging in the values, you can determine the gear ratio. It's essential to note that the gear ratio can be a positive or negative value, depending on the configuration of the gears.
- The gear ratio is calculated as a ratio of the output speed to the input speed.
- The formula (R + S) / S is used to calculate the gear ratio, where R is the number of teeth on the ring gear and S is the number of teeth on the sun gear.
- The gear ratio can be used to determine the torque and speed of the output shaft.
Types of Planetary Gears
There are several types of planetary gears, each with its own unique characteristics and applications. The single-stage planetary gear is the most common type, but there are also multi-stage planetary gears and differential planetary gears. Each type of planetary gear has its own gear ratio and efficiency.
- The single-stage planetary gear is the most common type, with a single sun gear and a single ring gear.
- The multi-stage planetary gear has multiple sun gears and ring gears, allowing for a higher gear ratio.
- The differential planetary gear is used to transmit power between two or more output shafts.
Advantages of Planetary Gears
Planetary gears have several advantages, including a high gear ratio, a compact design, and a high efficiency. They are also reliable and maintenance-free, making them a popular choice for many applications. The gear ratio of a planetary gear can be adjusted to meet the specific needs of the application.
- Planetary gears have a high gear ratio, making them suitable for applications where a high torque is required.
- The compact design of planetary gears makes them ideal for applications where space is limited.
- Planetary gears are reliable and maintenance-free, reducing the need for repairs and maintenance.
Applications of Planetary Gears
Planetary gears are used in a wide range of applications, including automotive, aerospace, and industrial. They are used to transmit power between the engine and the wheels in cars, and to transmit power between the turbine and the generator in power plants. The gear ratio of a planetary gear can be adjusted to meet the specific needs of the application.
- Planetary gears are used in automotive applications, such as transmissions and differentials.
- Planetary gears are used in aerospace applications, such as aircraft and spacecraft.
- Planetary gears are used in industrial applications, such as power plants and machine tools.
What is the planetary gearbox theory?
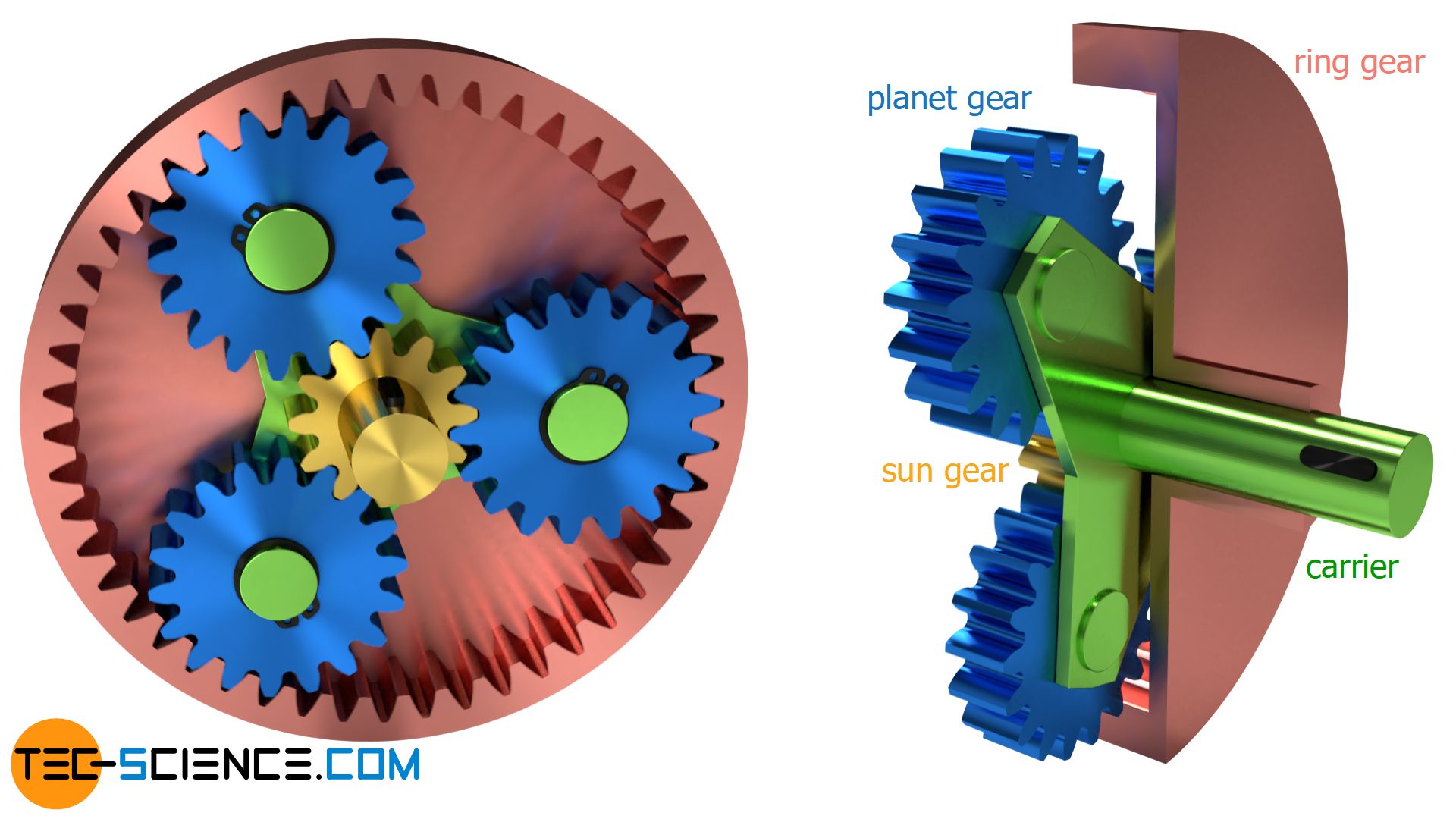
The planetary gearbox theory is a mechanical system that consists of a central sun gear, planet gears, and an internal ring gear. This system is designed to provide high torque and low speed ratios, making it ideal for applications such as robotics, aerospace, and industrial machinery. The planetary gearbox theory is based on the concept of epicyclic gearing, where the planet gears rotate around the central sun gear, while also rotating on their own axes.
Introduction to Planetary Gearbox Theory
The planetary gearbox theory is a complex system that requires a deep understanding of mechanical engineering and gear design. The system consists of a central sun gear, planet gears, and an internal ring gear, which work together to provide high torque and low speed ratios. Some key features of the planetary gearbox theory include:
- High torque density: The planetary gearbox system is capable of providing high torque density, making it ideal for applications where space is limited.
- Low speed ratios: The system is designed to provide low speed ratios, making it suitable for applications where high precision is required.
- High efficiency: The planetary gearbox system is highly efficient, with minimal energy loss due to friction and heat generation.
Components of a Planetary Gearbox
The planetary gearbox system consists of several key components, including the central sun gear, planet gears, and internal ring gear. Each component plays a critical role in the operation of the system, and must be designed and manufactured with precision to ensure optimal performance. Some key components of a planetary gearbox include:
- Central sun gear: The central sun gear is the central component of the planetary gearbox system, and is responsible for transmitting torque and speed to the planet gears.
- Planet gears: The planet gears are the gears that rotate around the central sun gear, and are responsible for transmitting torque and speed to the internal ring gear.
- Internal ring gear: The internal ring gear is the outer component of the planetary gearbox system, and is responsible for providing support and stability to the planet gears.
Operating Principle of a Planetary Gearbox
The planetary gearbox system operates on the principle of epicyclic gearing, where the planet gears rotate around the central sun gear, while also rotating on their own axes. This motion creates a complex gear train that is capable of providing high torque and low speed ratios. Some key features of the operating principle of a planetary gearbox include:
- Epicyclic gearing: The planetary gearbox system uses epicyclic gearing to provide high torque and low speed ratios.
- Compound gear trains: The system uses compound gear trains to provide high precision and accuracy.
- Optimal gear design: The planetary gearbox system requires optimal gear design to ensure maximum efficiency and minimum energy loss.
Applications of Planetary Gearbox Theory
The planetary gearbox theory has a wide range of applications in industrial machinery, aerospace, and robotics. The system is ideal for applications where high torque and low speed ratios are required, and where space is limited. Some key applications of planetary gearbox theory include:
- Industrial machinery: The planetary gearbox system is used in industrial machinery such as conveyors, pumps, and generators.
- Aerospace: The system is used in aerospace applications such as aircraft, spacecraft, and satellites.
- Robotics: The planetary gearbox system is used in robotics applications such as robot arms, grippers, and actuators.
Advantages and Limitations of Planetary Gearbox Theory
The planetary gearbox theory has several advantages and limitations that must be considered when designing and implementing the system. Some key advantages and limitations of planetary gearbox theory include:
- High torque density: The planetary gearbox system is capable of providing high torque density, making it ideal for applications where space is limited.
- Low speed ratios: The system is designed to provide low speed ratios, making it suitable for applications where high precision is required.
- Complexity: The planetary gearbox system is complex and requires specialized knowledge and expertise to design and implement.
Frequently Asked Questions (FAQs)
What are Planetary Epicyclic Gear Ratios and their importance in engineering applications?
Planetary epicyclic gear ratios are a type of gear system that consists of a central sun gear, multiple planet gears, and an outer ring gear. The sun gear is typically the input gear, while the planet gears rotate around the sun gear and are connected to a carrier. The ring gear is the outer gear that surrounds the planet gears. The planetary epicyclic gear ratios are used to achieve a high torque-to-weight ratio, making them ideal for applications where space and weight are limited. These gear systems are commonly used in aerospace, automotive, and industrial applications, where high precision and reliability are required. The equations used to calculate the gear ratios are complex and involve the number of teeth on each gear, the pitch diameter, and the pressure angle.
How do you calculate the gear ratios for a planetary epicyclic gear system using equations and calculators?
Calculating the gear ratios for a planetary epicyclic gear system involves using mathematical equations that take into account the number of teeth on each gear, the pitch diameter, and the pressure angle. The gear ratio is calculated by dividing the output speed by the input speed. The equations used to calculate the gear ratios are typically based on the kinematics of the gear system and involve the use of trigonometry and algebra. Calculators can be used to simplify the calculations and provide quick and accurate results. The input parameters required for the calculations include the number of teeth on each gear, the pitch diameter, and the pressure angle. The output of the calculations is the gear ratio, which can be used to determine the torque and speed of the output shaft.
What are the advantages and disadvantages of using planetary epicyclic gear ratios in engineering applications?
The advantages of using planetary epicyclic gear ratios include their high torque-to-weight ratio, making them ideal for applications where space and weight are limited. They also provide a high precision and reliability, making them suitable for applications where accuracy and consistency are critical. Additionally, planetary epicyclic gear ratios can be designed to provide a high reduction ratio, making them ideal for applications where a high torque is required. However, the disadvantages of using planetary epicyclic gear ratios include their complexity, which can make them more difficult to design and manufacture. They also require precise alignment and assembly, which can be time-consuming and costly. Furthermore, planetary epicyclic gear ratios can be noisy and vibration-prone, which can be a problem in applications where quiet operation is required.
How do you design and optimize planetary epicyclic gear ratios for specific engineering applications using calculators and software?
Designing and optimizing planetary epicyclic gear ratios for specific engineering applications involves using calculators and software to analyze the gear system and determine the optimal gear ratio. The design process typically involves inputting the requirements of the application, such as the torque and speed requirements, into the calculator or software. The calculator or software then uses algorithms and equations to determine the optimal gear ratio and gear design. The output of the design process is a detailed design of the gear system, including the number of teeth on each gear, the pitch diameter, and the pressure angle. The design can then be optimized using iterative calculations and sensitivity analysis to ensure that the gear system meets the requirements of the application. Software such as computer-aided design (CAD) and finite element analysis (FEA) can be used to simulate the behavior of the gear system and validate the design.
Deja una respuesta

Entradas Relacionadas