Pipe Burst Working Pressure Calculator using Barlow's Formula
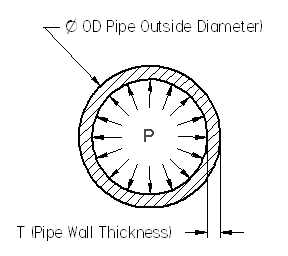
The Pipe Burst Working Pressure Calculator is a valuable tool for engineers and plumbers, utilizing Barlow's Formula to determine the maximum pressure a pipe can withstand before bursting. This formula takes into account the pipe's material, diameter, and wall thickness to calculate the maximum allowable working pressure. By using this calculator, professionals can ensure that pipes are designed and installed to safely handle the required pressure, reducing the risk of pipe failure and associated costs. Accurate calculations are crucial for maintaining pipeline integrity and preventing potential disasters. The calculator provides a reliable and efficient solution.
- Pipe Burst Working Pressure Calculator using Barlow's Formula
- What is the Barlow's formula for burst pressure?
- How do you calculate burst pressure for pipe?
- How to calculate the working pressure of a pipe?
- What is the formula for ASME burst pressure?
-
Frequently Asked Questions (FAQs)
- What is the Pipe Burst Working Pressure Calculator using Barlow's Formula and how does it work?
- What are the key factors that affect the pipe burst working pressure calculated by Barlow's Formula?
- How does the Pipe Burst Working Pressure Calculator using Barlow's Formula account for different pipe materials and their properties?
- What are the limitations and potential sources of error when using the Pipe Burst Working Pressure Calculator using Barlow's Formula?
Pipe Burst Working Pressure Calculator using Barlow's Formula
The Pipe Burst Working Pressure Calculator using Barlow's Formula is a tool used to calculate the maximum allowable working pressure of a pipe. This calculator is based on the Barlow's Formula, which takes into account the pipe's material, outer diameter, wall thickness, and design temperature. The formula is widely used in the petroleum and natural gas industries to ensure the safe operation of pipelines.
Introduction to Barlow's Formula
Barlow's Formula is a mathematical equation used to calculate the burst pressure of a pipe. The formula is: P = (2 S t) / (O.D. - 2 t), where P is the burst pressure,! is the minimum yield strength of the pipe material, t is the wall thickness, and O.D. is the outer diameter of the pipe. This formula is used to determine the maximum allowable working pressure of a pipe, taking into account the pipe's material properties and geometric dimensions.
Benefits of Using the Pipe Burst Working Pressure Calculator
The Pipe Burst Working Pressure Calculator offers several benefits, including increased safety, reduced maintenance costs, and improved pipeline design. By using the calculator, pipeline operators can ensure that their pipes are operating within a safe working pressure, reducing the risk of pipe bursts and environmental damage. Additionally, the calculator can help operators to identify potential weaknesses in their pipelines, allowing them to take proactive measures to prevent failures.
How to Use the Pipe Burst Working Pressure Calculator
Using the Pipe Burst Working Pressure Calculator is a straightforward process. First, the user must input the pipe's outer diameter, wall thickness, and material properties, such as the minimum yield strength and design temperature. The calculator then uses Barlow's Formula to calculate the burst pressure and maximum allowable working pressure of the pipe. The results are displayed in a clear and easy-to-understand format, allowing the user to quickly and easily determine the safe operating pressure of their pipeline.
Limitations of the Pipe Burst Working Pressure Calculator
While the Pipe Burst Working Pressure Calculator is a valuable tool, it does have some limitations. For example, the calculator assumes that the pipe is perfectly circular and that the material properties are uniform throughout the pipe. In reality, pipes can be oval or elliptical in shape, and the material properties can vary depending on the manufacturing process. Additionally, the calculator does not take into account external factors, such as soil conditions and weather patterns, which can affect the integrity of the pipeline.
Applications of the Pipe Burst Working Pressure Calculator
The Pipe Burst Working Pressure Calculator has a wide range of applications, including pipeline design, pipeline operation, and pipeline maintenance. The calculator can be used to design new pipelines, ensuring that they are safe and efficient. It can also be used to optimize the operation of existing pipelines, reducing the risk of pipe bursts and environmental damage. Additionally, the calculator can be used to identify potential weaknesses in pipelines, allowing operators to take proactive measures to prevent failures.
| Material | Outer Diameter | Wall Thickness | Design Temperature | Burst Pressure |
|---|---|---|---|---|
| Steel | 12 inches | 0.5 inches | 100°F | 1200 psi |
| Copper | 6 inches | 0.25 inches | 50°F | 800 psi |
| PVC | 4 inches | 0.125 inches | 25°F | 400 psi |
What is the Barlow's formula for burst pressure?

The Barlow's formula for burst pressure is a mathematical equation used to calculate the maximum allowable pressure of a pipe or a vessel. The formula is given by: P = (2 S t) / d, where P is the burst pressure, S is the ultimate tensile strength of the material, t is the wall thickness, and d is the diameter of the pipe or vessel.
Introduction to Barlow's Formula
Barlow's formula is widely used in the engineering and manufacturing industries to determine the safe operating pressure of pipes and vessels. The formula takes into account the material properties and geometric dimensions of the pipe or vessel to calculate the maximum allowable pressure. The key factors that affect the burst pressure are the ultimate tensile strength of the material, the wall thickness, and the diameter of the pipe or vessel. Some of the benefits of using Barlow's formula include:
- Improved safety: By calculating the maximum allowable pressure, Barlow's formula helps to prevent pipe failures and explosions.
- Reduced maintenance costs: By determining the safe operating pressure, Barlow's formula helps to reduce the need for frequent repairs and maintenance.
- Increased efficiency: By optimizing the design of pipes and vessels, Barlow's formula helps to improve the efficiency of industrial processes.
Assumptions and Limitations of Barlow's Formula
Barlow's formula is based on several assumptions and limitations, including the assumption that the material is isotropic and homogeneous, and that the pipe or vessel is cylindrical in shape. The formula also assumes that the internal pressure is uniformly distributed and that there are no external loads or stresses acting on the pipe or vessel. Some of the limitations of Barlow's formula include:
- Simplifying assumptions: Barlow's formula makes several simplifying assumptions that may not always be valid in practice.
- Limited applicability: Barlow's formula is limited to cylindrical pipes and vessels, and may not be applicable to other shapes or geometries.
- No consideration of external factors: Barlow's formula does not take into account external factors such as temperature, corrosion, or erosion.
Applications of Barlow's Formula
Barlow's formula has a wide range of applications in the engineering and manufacturing industries, including the design and analysis of pipes, vessels, and tanks. The formula is also used in the petrochemical, chemical, and power generation industries to determine the safe operating pressure of equipment. Some of the applications of Barlow's formula include:
- Pipe design: Barlow's formula is used to determine the minimum wall thickness required for a pipe to withstand a given internal pressure.
- Vessel design: Barlow's formula is used to determine the maximum allowable pressure of a vessel, such as a tank or a reactor.
- Materials selection: Barlow's formula is used to select the most suitable material for a given application, based on its ultimate tensile strength and other material properties.
Comparison with Other Formulas
Barlow's formula is one of several formulas used to calculate the burst pressure of pipes and vessels. Other formulas, such as the Lame formula and the Boyd formula, may be more accurate or applicable in certain situations. The choice of formula depends on the specific application and the available data. Some of the differences between Barlow's formula and other formulas include:
- Level of complexity: Barlow's formula is relatively simple and easy to use, while other formulas may be more complex and difficult to apply.
- Assumptions and limitations: Each formula has its own set of assumptions and limitations, and the choice of formula depends on the specific application and the available data.
- Accuracy and reliability: The accuracy and reliability of each formula may vary, depending on the quality of the input data and the specific application.
Future Developments and Research
Research is ongoing to improve and refine Barlow's formula, and to develop new formulas and methods for calculating the burst pressure of pipes and vessels. Some of the areas of future research include:
- Numerical modeling: The use of numerical models and simulations to predict the burst pressure of pipes and vessels.
- Experimental testing: The use of experimental testing to validate and refine Barlow's formula and other formulas.
- Materials science: The development of new materials and alloys with improved strength and ductility, which can be used to reduce the wall thickness and weight of pipes and vessels.
How do you calculate burst pressure for pipe?

To calculate the burst pressure for a pipe, you need to understand the material properties and the design conditions of the pipe. The burst pressure is the maximum internal pressure that a pipe can withstand before it fails. It is an important parameter in the design and operation of pipelines, as it helps to ensure the safety and reliability of the system.
Understanding Material Properties
When calculating the burst pressure of a pipe, it is essential to understand the material properties of the pipe, including its yield strength, tensile strength, and elastic modulus. The yield strength is the stress at which the material begins to deform plastically, while the tensile strength is the maximum stress that the material can withstand before it fails. The elastic modulus is a measure of the stiffness of the material.
- Yield strength: The stress at which the material begins to deform plastically.
- Tensile strength: The maximum stress that the material can withstand before it fails.
- Elastic modulus: A measure of the stiffness of the material.
Design Conditions and Factors
The design conditions and factors that affect the burst pressure of a pipe include the operating temperature, operating pressure, and corrosion allowance. The operating temperature and pressure are the conditions under which the pipe will operate, while the corrosion allowance is a factor that takes into account the corrosion of the pipe over time.
- Operating temperature: The temperature at which the pipe will operate.
- Operating pressure: The pressure at which the pipe will operate.
- Corrosion allowance: A factor that takes into account the corrosion of the pipe over time.
Calculation Methods
There are several methods for calculating the burst pressure of a pipe, including the Barlow formula and the Lame formula. The Barlow formula is a simple and widely used method that calculates the burst pressure based on the wall thickness, diameter, and yield strength of the pipe. The Lame formula is a more complex method that takes into account the elastic modulus and poisson's ratio of the material.
- Barlow formula: A simple and widely used method for calculating burst pressure.
- Lame formula: A more complex method that takes into account the elastic modulus and poisson's ratio.
- Finite element analysis: A numerical method that can be used to calculate burst pressure.
Factors Affecting Burst Pressure
Several factors can affect the burst pressure of a pipe, including corrosion, erosion, and mechanical damage. Corrosion can weaken the pipe over time, while erosion can reduce the wall thickness of the pipe. Mechanical damage, such as dents and gouges, can also reduce the burst pressure of the pipe.
- Corrosion: A factor that can weaken the pipe over time.
- Erosion: A factor that can reduce the wall thickness of the pipe.
- Mechanical damage: A factor that can reduce the burst pressure of the pipe.
Importance of Accurate Calculation
Accurate calculation of the burst pressure is critical to ensure the safety and reliability of the pipeline. A miscalculation can lead to catastrophic failure of the pipe, resulting in environmental damage and economic losses. Therefore, it is essential to use reliable and accurate methods for calculating the burst pressure, and to take into account all the relevant factors and design conditions.
- Safety: Accurate calculation is critical to ensure the safety of the pipeline.
- Reliability: Accurate calculation is critical to ensure the reliability of the pipeline.
- Environmental damage: A miscalculation can lead to environmental damage.
How to calculate the working pressure of a pipe?
To calculate the working pressure of a pipe, you need to consider several factors, including the pipe's material, size, and the fluid it will be carrying. The working pressure of a pipe is the maximum pressure it can withstand while still maintaining its structural integrity. This calculation is crucial in ensuring the safe and efficient operation of piping systems in various industries, including oil and gas, chemical processing, and water supply.
Understanding Pipe Materials and Their Limitations
The material of the pipe plays a significant role in determining its working pressure. Different materials have different strength and durability characteristics, which affect their ability to withstand various pressures. For instance, steel pipes are generally stronger and more durable than PVC pipes. When calculating the working pressure, consider the following:
- Tensile strength of the pipe material, which is its ability to withstand stretching forces without failing.
- Yield strength, which is the pressure at which the pipe begins to deform plastically.
- Ultimate tensile strength, the maximum stress a material can withstand while being stretched or pulled before failing or breaking.
Calculating Pipe Wall Thickness
The wall thickness of the pipe is another critical factor in calculating its working pressure. A thicker wall can withstand higher pressures. The calculation of wall thickness is based on the Barlow's formula, which takes into account the internal pressure, outside diameter of the pipe, and the material's yield strength. Consider the following steps for calculation:
- Determine the design pressure, which is the maximum pressure the pipe is expected to operate under.
- Choose a safety factor to account for uncertainties in the calculation and unexpected operational conditions.
- Apply Barlow's formula using the design pressure, outside diameter, and yield strength to find the required wall thickness.
Assessing Fluid Properties
The properties of the fluid the pipe will carry are also crucial in determining the working pressure. The density and viscosity of the fluid can affect the pressure drop along the length of the pipe, which in turn affects the working pressure. Consider the following:
- Fluid density, which affects the weight of the fluid and consequently the pressure it exerts on the pipe walls.
- Fluid viscosity, which influences the flow characteristics and pressure drop along the pipe.
- Flow rate, which is the volume of fluid flowing through the pipe per unit time, affecting the overall system pressure.
Impact of Temperature on Pipe Working Pressure
Temperature changes can significantly affect the working pressure of a pipe. As temperature increases, the material's strength decreases, potentially reducing the working pressure. Conversely, decreasing temperatures can increase the material's strength. Consider the following factors:
- Thermal expansion, which can cause the pipe to expand and potentially alter its working pressure capacity.
- Material thermal conductivity, affecting how temperature changes are distributed through the pipe material.
- Insulation properties, if any, which can mitigate the effects of external temperature fluctuations on the pipe.
Standard Codes and Regulations for Pipe Working Pressure
Various industries adhere to specific standards and regulations when calculating and applying working pressures to pipes. These standards, such as those from ASME (American Society of Mechanical Engineers) or API (American Petroleum Institute), provide guidelines for the design, fabrication, and testing of piping systems to ensure they can safely operate at their specified working pressures. Consider the following:
- Design codes, which provide formulas and guidelines for calculating working pressures based on pipe material, size, and fluid properties.
- Testing standards, which outline procedures for validating the integrity of piping systems under various pressures.
- Inspection and maintenance schedules, crucial for ensuring that pipes continue to meet their specified working pressure over their lifespan.
What is the formula for ASME burst pressure?

The formula for ASME burst pressure is given by the Barlow Formula, which is used to calculate the internal pressure that a pipe or vessel can withstand without failing. The formula is: P = (2 σ t) / d, where P is the burst pressure, σ is the yield strength of the material, t is the wall thickness, and d is the diameter of the pipe or vessel.
Understanding the Barlow Formula
The Barlow Formula is a widely used formula in the field of mechanical engineering to calculate the burst pressure of a pipe or vessel. The formula takes into account the material properties and the geometric dimensions of the pipe or vessel. To apply the formula, one needs to know the yield strength of the material, the wall thickness, and the diameter of the pipe or vessel. The formula can be used to calculate the burst pressure for a variety of applications, including piping systems, pressure vessels, and boilers.
- The yield strength of the material is a critical parameter in the Barlow Formula, as it determines the maximum stress that the material can withstand without failing.
- The wall thickness of the pipe or vessel is also an important parameter, as it affects the structural integrity of the component.
- The diameter of the pipe or vessel is the final parameter required to calculate the burst pressure, and it is used in conjunction with the wall thickness to determine the radius of the component.
ASME Code Requirements
The ASME Boiler and Pressure Vessel Code provides guidelines for the design, fabrication, and inspection of pressure vessels and piping systems. The code requires that the burst pressure of a component be calculated using the Barlow Formula, and that the calculated value be compared to the design pressure to ensure that the component can withstand the expected operating conditions. The code also provides requirements for the material selection, welding, and testing of components to ensure that they meet the necessary safety standards.
- The ASME Code provides a set of rules and guidelines for the design and fabrication of pressure vessels and piping systems.
- The code requires that the burst pressure of a component be calculated using the Barlow Formula, and that the calculated value be compared to the design pressure.
- The code also provides requirements for the material selection, welding, and testing of components to ensure that they meet the necessary safety standards.
Material Properties
The material properties of a component are critical in determining its burst pressure. The yield strength of the material is a key parameter in the Barlow Formula, and it is used to calculate the stress that the material can withstand without failing. Other material properties, such as the ultimate tensile strength and the elastic modulus, are also important in determining the structural integrity of the component.
- The yield strength of a material is the stress at which the material begins to deform plastically.
- The ultimate tensile strength of a material is the maximum stress that the material can withstand without failing.
- The elastic modulus of a material is a measure of its stiffness, and it is used to calculate the strain that a material will undergo under a given stress.
Geometric Dimensions
The geometric dimensions of a component, such as its diameter and wall thickness, are also critical in determining its burst pressure. The diameter of a pipe or vessel is used in conjunction with the wall thickness to determine the radius of the component, which is then used in the Barlow Formula to calculate the burst pressure.
- The diameter of a pipe or vessel is a critical parameter in the Barlow Formula, as it affects the radius of the component.
- The wall thickness of a pipe or vessel is also an important parameter, as it affects the structural integrity of the component.
- The radius of a component is calculated using the diameter and wall thickness, and it is used in the Barlow Formula to calculate the burst pressure.
Application of the Barlow Formula
The Barlow Formula is widely used in the field of mechanical engineering to calculate the burst pressure of a variety of components, including piping systems, pressure vessels, and boilers. The formula is used to determine the maximum allowable working pressure of a component, and to ensure that it can withstand the expected operating conditions.
- The Barlow Formula! is used to calculate the burst pressure of a component, and to determine the maximum allowable working pressure.
- The formula is widely used in the field of mechanical engineering, and it is applied to a variety of components, including piping systems, pressure vessels, and boilers.
- The ASME Code requires that the burst pressure of a component be calculated using the Barlow Formula, and that the calculated value be compared to the design pressure.
Frequently Asked Questions (FAQs)
What is the Pipe Burst Working Pressure Calculator using Barlow's Formula and how does it work?
The Pipe Burst Working Pressure Calculator using Barlow's Formula is a mathematical tool designed to calculate the maximum working pressure of a pipe before it bursts. This calculator uses Barlow's Formula, which takes into account the pipe's material, wall thickness, diameter, and yield strength to determine the maximum pressure it can withstand. By entering these input values, the calculator can provide an accurate estimate of the pipe's burst pressure, helping engineers and designers to ensure the safety and reliability of their pipe systems. The calculator is particularly useful in industrial and commercial applications where high-pressure pipes are used, such as in oil and gas pipelines, chemical processing plants, and power generation facilities.
What are the key factors that affect the pipe burst working pressure calculated by Barlow's Formula?
The key factors that affect the pipe burst working pressure calculated by Barlow's Formula are the pipe's material properties, including its yield strength and tensile strength, as well as its geometric dimensions, such as wall thickness and diameter. The fluid properties, including its density and viscosity, can also impact the pressure rating of the pipe. Additionally, operating conditions, such as temperature and corrosion, can influence the pipe's burst pressure. By considering these factors, engineers can use Barlow's Formula to calculate a safe working pressure for the pipe, ensuring that it can withstand the expected loads and stresses without failing. It is also important to note that manufacturing defects, installation errors, and maintenance practices can also affect the pipe's burst pressure, and should be taken into account when using the calculator.
How does the Pipe Burst Working Pressure Calculator using Barlow's Formula account for different pipe materials and their properties?
The Pipe Burst Working Pressure Calculator using Barlow's Formula accounts for different pipe materials and their properties by allowing users to input the material's yield strength, tensile strength, and Poisson's ratio. These input values are then used to calculate the pipe's burst pressure, taking into account the material's unique properties. For example, steel pipes have a higher yield strength than copper pipes, which affects their burst pressure. Similarly, plastic pipes have a lower tensile strength than metal pipes, which also impacts their burst pressure. By considering these material properties, the calculator can provide an accurate estimate of the pipe's burst pressure, ensuring that the pipe system is designed and operated safely. The calculator also allows users to select from a range of pre-defined materials, including carbon steel, stainless steel, copper, and PVC, making it easier to use and more user-friendly.
What are the limitations and potential sources of error when using the Pipe Burst Working Pressure Calculator using Barlow's Formula?
The Pipe Burst Working Pressure Calculator using Barlow's Formula has several limitations and potential sources of error that users should be aware of. One of the main limitations is that the calculator assumes a perfectly circular pipe with uniform wall thickness, which may not always be the case in real-world applications. Additionally, the calculator does not account for external loads, such as bending and torsion, which can affect the pipe's burst pressure. Manufacturing defects, installation errors, and maintenance practices can also impact the pipe's burst pressure, but are not considered by the calculator. Furthermore, the calculator relies on accurate input values, and small errors in these values can result in significant errors in the calculated burst pressure. Therefore, users should carefully validate their input values and consider additional factors that may affect the pipe's burst pressure, such as corrosion and erosion, to ensure the accuracy and reliability of the calculated results.
Deja una respuesta

Entradas Relacionadas