Flat Plate Heat Transfer Convected Equation and Calculator

The flat plate heat transfer convection equation is a fundamental concept in thermodynamics, describing the heat transfer between a solid plate and a surrounding fluid. This phenomenon occurs in various engineering applications, including heat exchangers, electronic cooling systems, and aerospace engineering. The equation takes into account the fluid's properties, such as velocity, temperature, and density, to calculate the convective heat transfer coefficient. An online calculator can be used to simplify the calculation process, providing a quick and accurate estimate of the heat transfer rate. Understanding this equation is crucial for efficient thermal design.
- Understanding Flat Plate Heat Transfer Convected Equation and Calculator
- What is the equation for the flat plate heat exchanger?
- How do you calculate convection heat transfer?
- How do you calculate the heat transmission by convection?
- What is the convection coefficient of air at 20 °C?
-
Frequently Asked Questions (FAQs)
- What is the Flat Plate Heat Transfer Convected Equation and how is it used in engineering applications?
- How does the Flat Plate Heat Transfer Convected Equation and Calculator account for different flow regimes and fluid properties?
- What are the limitations and assumptions of the Flat Plate Heat Transfer Convected Equation and Calculator, and how can they be addressed?
- How can the Flat Plate Heat Transfer Convected Equation and Calculator be used in conjunction with other heat transfer equations and calculators to solve complex heat transfer problems?
Understanding Flat Plate Heat Transfer Convected Equation and Calculator
The flat plate heat transfer convected equation is a fundamental concept in the field of heat transfer, which is crucial in various engineering applications. This equation is used to calculate the convective heat transfer coefficient between a flat plate and a fluid flowing over it. The calculator used to solve this equation is an essential tool for engineers to determine the heat transfer rate and design efficient heat transfer systems.
Introduction to Convective Heat Transfer
Convective heat transfer occurs when a fluid flows over a surface, and heat is transferred between the surface and the fluid. The convective heat transfer coefficient is a measure of the rate at which heat is transferred between the surface and the fluid. The flat plate heat transfer convected equation is used to calculate this coefficient, which is essential in designing heat transfer systems such as heat exchangers, cooling systems, and heating systems.
Derivation of the Flat Plate Heat Transfer Convected Equation
The flat plate heat transfer convected equation is derived from the Navier-Stokes equations, which describe the motion of fluids. The equation is based on the assumption that the fluid flow is laminar and incompressible, and that the thermal boundary layer is much thinner than the free stream boundary layer. The equation is given by:
h = (k / x) Nu
where h is the convective heat transfer coefficient, k is the thermal conductivity of the fluid, x is the distance from the leading edge of the plate, and Nu is the Nusselt number.
Calculation of the Nusselt Number
The Nusselt number (Nu) is a dimensionless quantity that is used to calculate the convective heat transfer coefficient. The Nusselt number is calculated using the following equation:
Nu = (h x) / k
The Nusselt number is a function of the Reynolds number (Re) and the Prandtl number (Pr). The Reynolds number is a measure of the ratio of inertial forces to viscous forces, while the Prandtl number is a measure of the ratio of momentum diffusivity to thermal diffusivity.
Applications of the Flat Plate Heat Transfer Convected Equation
The flat plate heat transfer convected equation has numerous applications in various fields of engineering, including:
Aerospace engineering: to design heat shields and thermal protection systems for spacecraft and missiles
Automotive engineering: to design heat exchangers and cooling systems for vehicles
Chemical engineering: to design heat exchangers and reactors for chemical processes
Mechanical engineering: to design heat exchangers, cooling systems, and heating systems for buildings and industrial processes
Using a Calculator to Solve the Flat Plate Heat Transfer Convected Equation
A calculator can be used to solve the flat plate heat transfer convected equation by inputting the values of the thermal conductivity (k), the distance from the leading edge (x), and the Nusselt number (Nu). The calculator can then be used to calculate the convective heat transfer coefficient (h).
The following table provides a summary of the key parameters used in the flat plate heat transfer convected equation:
| Parameter | Description |
|---|---|
| h | Convective heat transfer coefficient |
| k | Thermal conductivity of the fluid |
| x | Distance from the leading edge of the plate |
| Nu | Nusselt number |
| Re | Reynolds number |
| Pr | Prandtl number |
These parameters are essential in understanding the flat plate heat transfer convected equation and using a calculator to solve it. The calculator can be used to determine the convective heat transfer coefficient, which is crucial in designing heat transfer systems. By understanding the flat plate heat transfer convected equation and using a calculator to solve it, engineers can design more efficient heat transfer systems.
What is the equation for the flat plate heat exchanger?
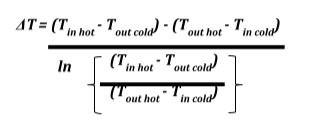
The equation for the flat plate heat exchanger is given by the log mean temperature difference (LMTD) method, which calculates the heat transfer rate between two fluids flowing through the heat exchanger. The equation is as follows: Q = U A LMTD, where Q is the heat transfer rate, U is the overall heat transfer coefficient, A is the heat transfer area, and LMTD is the log mean temperature difference between the two fluids.
Introduction to Flat Plate Heat Exchangers
Flat plate heat exchangers are compact and efficient heat transfer devices used in various industries, including chemical processing, food processing, and power generation. They consist of a series of flat plates with corrugated surfaces to enhance heat transfer. The plates are stacked together to form a compact unit, with gaskets or welds to seal the plates and prevent fluid leakage. The key features of flat plate heat exchangers include:
- High heat transfer coefficients due to the turbulent flow of fluids
- Low pressure drop due to the smooth surface of the plates
- Compact design, making them ideal for space-constrained applications
Heat Transfer Mechanisms in Flat Plate Heat Exchangers
The heat transfer mechanisms in flat plate heat exchangers involve convection, conduction, and radiation. The convective heat transfer coefficient is a function of the fluid velocity, temperature, and physical properties. The conductive heat transfer occurs through the plate material, and the radiative heat transfer is negligible in most cases. The heat transfer mechanisms can be enhanced by using fins or corrugations on the plate surface. The key factors that influence heat transfer in flat plate heat exchangers include:
- Fluid velocity and turbulence
- Plate surface roughness and corrugation
- Fluid physical properties, such as viscosity and thermal conductivity
Design Considerations for Flat Plate Heat Exchangers
The design of flat plate heat exchangers involves optimizing various parameters, including the plate size, spacing, and material, to achieve the desired heat transfer rate and pressure drop. The design considerations include the flow arrangement, plate geometry, and sealing system. The flow arrangement can be counterflow or parallel flow, and the plate geometry can be smooth or corrugated. The key design considerations for flat plate heat exchangers include:
- Plate size and spacing to achieve the desired heat transfer area
- Plate material and thickness to minimize pressure drop and cost
- Sealing system to prevent fluid leakage and ensure reliability
Applications of Flat Plate Heat Exchangers
Flat plate heat exchangers have a wide range of applications in various industries, including chemical processing, food processing, and power generation. They are used for heating, cooling, and heat recovery applications. The key advantages of flat plate heat exchangers include their compact design, high efficiency, and low maintenance requirements. The typical applications of flat plate heat exchangers include:
- Heat recovery from waste heat streams
- Cooling of process fluids and equipment
- Heating of process fluids and products
Operation and Maintenance of Flat Plate Heat Exchangers
The operation and maintenance of flat plate heat exchangers are crucial to ensure their reliability and efficiency. The operating conditions, such as fluid velocity and temperature, must be carefully monitored to prevent fouling, corrosion, and erosion. The maintenance activities include cleaning, inspecting, and replacing worn-out parts. The key factors that affect the operation and maintenance of flat plate heat exchangers include:
- Fluid quality and treatment to prevent fouling and corrosion
- Operational parameters, such as flow rate and temperature
- Maintenance schedule and procedures to ensure reliability and efficiency
How do you calculate convection heat transfer?
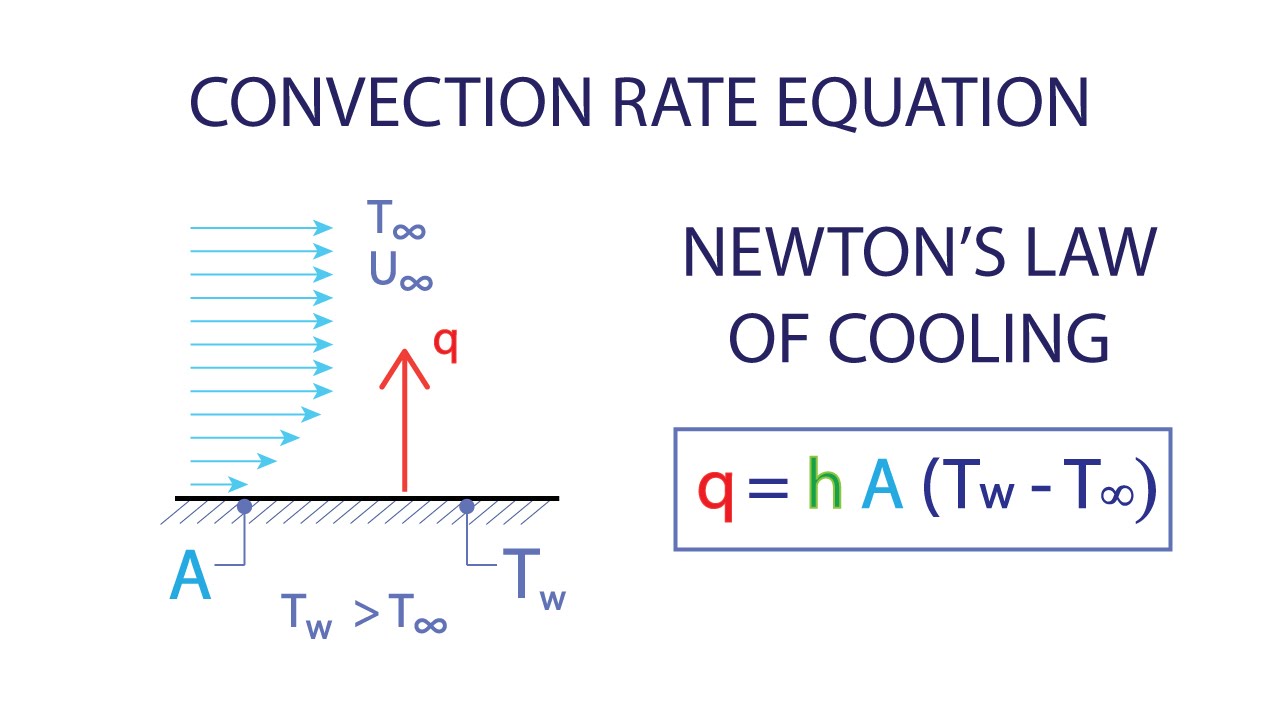
To calculate convection heat transfer, you need to understand the principles of fluid dynamics and heat transfer. Convection heat transfer occurs when there is a temperature difference between a surface and a fluid, such as air or water, in contact with it. The heat transfer rate can be calculated using the convection heat transfer coefficient, which depends on the fluid properties, surface roughness, and flow velocity.
Introduction to Convection Heat Transfer
Convection heat transfer is a complex process that involves the motion of fluid particles and the transfer of heat energy. To calculate convection heat transfer, you need to consider the thermodynamic properties of the fluid, such as density, viscosity, and specific heat! capacity. The calculation involves the following steps:
- Determine the temperature difference between the surface and the fluid
- Calculate the convection heat transfer coefficient using empirical correlations or numerical simulations
- Apply the convective heat transfer equation to calculate the heat transfer rate
Convection Heat Transfer Coefficient
The convection heat transfer coefficient is a key parameter in calculating convection heat transfer. It depends on the fluid properties, surface roughness, and flow velocity. The coefficient can be calculated using empirical correlations, such as the Nusselt number, or numerical simulations, such as Computational Fluid Dynamics (CFD). The calculation involves:
- Determining the Reynolds number to establish the flow regime
- Calculating the Prandtl number to determine the fluid thermal properties
- Applying the Nusselt number correlation to calculate the convection heat transfer coefficient
Turbulent Flow and Convection Heat Transfer
Turbulent flow is a common occurrence in convection heat transfer, where the fluid motion is chaotic and unpredictable. In turbulent flow, the convection heat transfer coefficient is higher than in laminar flow, due to the increased mixing and turbulence. To calculate convection heat transfer in turbulent flow, you need to consider the turbulence models, such as the k-ε model, and the near-wall treatment. The calculation involves:
- Calculating the turbulent kinetic energy and dissipation rate
- Applying the turbulence model to calculate the convection heat transfer coefficient
- Using the near-wall treatment to account for the wall-bounded flow
Natural Convection and Convection Heat Transfer
Natural convection occurs when there is a temperature difference between a surface and a fluid, without any forced flow. In natural convection, the convection heat transfer coefficient is lower than in forced convection, due to the lower flow velocities. To calculate convection heat transfer in natural convection, you need to consider the Grashof number and the Rayleigh number. The calculation involves:
- Calculating the Grashof number to determine the buoyancy-driven flow
- Applying the Rayleigh number correlation to calculate the convection heat transfer coefficient
- Using the natural convection correlation to calculate the heat transfer rate
Forced Convection and Convection Heat Transfer
Forced convection occurs when there is a forced flow of fluid over a surface, such as in a heat exchanger or a pipe flow. In forced convection, the convection heat transfer coefficient is higher than in natural convection, due to the higher flow velocities. To calculate convection heat transfer in forced convection, you need to consider the Reynolds number and the Nusselt number. The calculation involves:
- Calculating the Reynolds number to determine the flow regime
- Applying the Nusselt number correlation to calculate the convection heat transfer coefficient
- Using the forced convection correlation to calculate the heat transfer rate
How do you calculate the heat transmission by convection?

To calculate the heat transmission by convection, you need to understand the principles of convective heat transfer. This process involves the transfer of heat between a solid surface and a fluid (liquid or gas) due to the movement of the fluid. The calculation of heat transmission by convection can be complex, but it is essential in various engineering applications, such as designing heating and cooling systems.
Understanding the Convection Coefficient
The convection coefficient (h) is a critical parameter in calculating the heat transmission by convection. It represents the rate of heat transfer between the solid surface and the fluid. To determine the convection coefficient, you need to consider factors such as the fluid properties (density, viscosity, and thermal conductivity), the surface geometry, and the flow velocity. The convection coefficient can be calculated using various correlations and empirical formulas, which are often specific to the particular application.
- The Nusselt number (Nu) is a dimensionless quantity that is used to calculate the convection coefficient.
- The Reynolds number (Re) is another dimensionless quantity that is used to determine the flow regime (laminar or turbulent).
- The Prandtl number (Pr) is a dimensionless quantity that is used to calculate the thermal conductivity of the fluid.
Calculating the Heat Transfer Rate
The heat transfer rate (Q) by convection can be calculated using the Newton's law of cooling, which states that the heat transfer rate is proportional to the temperature difference between the solid surface and the fluid. The heat transfer coefficient (U) is another important parameter that is used to calculate the heat transfer rate.
- The heat transfer coefficient (U) is a measure of the overall heat transfer resistance between the solid surface and the fluid.
- The temperature difference (ΔT) is the driving force behind the heat transfer process.
- The surface area (A) is the area over which the heat transfer occurs.
Factors Affecting Convection Heat Transfer
Several factors can affect the convection heat transfer, including the fluid properties, surface geometry, and flow velocity. The viscosity and thermal conductivity of the fluid can significantly impact the convection coefficient.
- The fluid viscosity can affect the flow regime and the convection coefficient.
- The surface roughness can also affect the convection coefficient by increasing the turbulence of the flow.
- The flow velocity can significantly impact the convection coefficient, with higher velocities resulting in higher coefficients.
Applications of Convection Heat Transfer
The convection heat transfer has numerous applications in various fields, including engineering, architecture, and science. It is used to design heating and cooling systems, such as heat exchangers, radiators, and air conditioning systems.
- The heat exchangers are used to transfer heat between two fluids, often in power plants and industrial processes.
- The radiators are used to transfer heat from a fluid to a solid surface, often in automotive and aerospace applications.
- The air conditioning systems are used to transfer heat from a building to the outside environment, often using convection and radiation.
Challenges and Limitations of Convection Heat Transfer
The convection heat transfer has several challenges and limitations, including the complexity of the flow and the uncertainty of the convection coefficient. The turbulence of the flow can make it difficult to predict the convection coefficient, and the surface roughness can increase the uncertainty of the coefficient.
- The complexity of the flow can make it challenging to predict the convection coefficient and the heat transfer rate.
- The uncertainty of the convection coefficient can affect the accuracy of the heat transfer calculations.
- The experimental techniques can be used to measure the convection coefficient and the heat transfer rate, but they can be time-consuming and expensive.
What is the convection coefficient of air at 20 °C?
The convection coefficient of air at 20 °C is a measure of the rate at which heat is transferred from a surface to the surrounding air. This coefficient is typically denoted by the symbol h and is expressed in units of Watts per square meter per Kelvin (W/m²K). The convection coefficient of air at 20 °C can be calculated using various formulas and correlations, which take into account factors such as the air velocity, surface roughness, and temperature difference between the surface and the air.
Introduction to Convection Coefficient
The convection coefficient is a critical parameter in the design of heat transfer systems, including heating and cooling systems. The convection coefficient of air at 20 °C is typically in the range of 5-10 W/m²K, depending on the specific conditions. The calculation of the convection coefficient involves the use of dimensionless numbers, such as the Nusselt number and the Reynolds number. Some of the key factors that affect the convection coefficient include:
- Air velocity: The velocity of the air moving past the surface can significantly impact the convection coefficient.
- Surface roughness: The roughness of the surface can affect the turbulence of the air flow, which in turn affects the convection coefficient.
- Temperature difference: The temperature difference between the surface and the air is a key factor in determining the convection coefficient.
Calculation Methods for Convection Coefficient
There are several methods for calculating the convection coefficient, including empirical correlations and numerical simulations. The choice of method depends on the specific conditions and the desired level of accuracy. Some common methods include the use of laminar flow and turbulent flow correlations, as well as computational fluid dynamics (CFD) simulations. The calculation of the convection coefficient requires a good understanding of the underlying physics and mathematics. Some of the key considerations include:
- Flow regime: The flow regime, whether laminar or turbulent, can significantly impact the convection coefficient.
- Surface geometry: The geometry of the surface, including the shape and size, can affect the convection coefficient.
- Fluid properties: The properties of the fluid, including the density, viscosity, and thermal conductivity, can impact the convection coefficient.
Factors Affecting Convection Coefficient
There are several factors that can affect the convection coefficient, including air velocity, surface roughness, and temperature difference. The convection coefficient can also be affected by other factors, such as humidity and air pressure. The impact of these factors can be significant, and must be carefully considered in the design of heat transfer systems. Some of the key factors include:
- Thermal conductivity: The thermal conductivity of the surface and the air can affect the convection coefficient.
- Viscosity: The viscosity of the air can impact the convection coefficient, particularly in laminar flow regimes.
- Prandtl number: The Prandtl number, which is a measure of the ratio of momentum diffusivity to thermal diffusivity, can also affect the convection coefficient.
Applications of Convection Coefficient
The convection coefficient has a wide range of practical applications, including the design of heating and cooling systems, electronic cooling systems, and chemical processing equipment. The convection coefficient is also used in the analysis of thermal comfort and indoor air quality. Some of the key applications include:
- Building design: The convection coefficient is used in the design of building envelopes and HVAC systems.
- Electronics cooling: The convection coefficient is used in the design of electronic cooling systems, including heat sinks and fans.
- Chemical processing: The convection coefficient is used in the design of chemical processing equipment, including reactors and heat exchangers.
Measurement Techniques for Convection Coefficient
There are several techniques for measuring the convection coefficient, including experimental methods and numerical simulations. The choice of method depends on the specific conditions and the desired level of accuracy. Some common methods include the use of hot wire anemometry and infrared thermography. The measurement of the convection coefficient requires a good understanding of the underlying physics and mathematics. Some of the key considerations include:
- Sensor accuracy: The accuracy of the sensors used to measure the convection coefficient can significantly impact the results.
- Flow uniformity: The uniformity of the flow can affect the measurement of the convection coefficient.
- Surface preparation: The preparation of the surface, including the cleanliness and roughness, can impact the measurement of the convection coefficient.
Frequently Asked Questions (FAQs)
What is the Flat Plate Heat Transfer Convected Equation and how is it used in engineering applications?
The Flat Plate Heat Transfer Convected Equation is a mathematical formula used to calculate the convective heat transfer coefficient between a flat plate and a surrounding fluid. This equation is crucial in various engineering applications, including aerospace, chemical processing, and electronic cooling. The equation takes into account the velocity of the fluid, the temperature difference between the plate and the fluid, and the physical properties of the fluid, such as density, specific heat capacity, and thermal conductivity. By using this equation, engineers can design and optimize systems that involve heat transfer, ensuring efficient and reliable operation. The convected equation is particularly useful in situations where forced convection is present, such as in heat exchangers or aircraft.
How does the Flat Plate Heat Transfer Convected Equation and Calculator account for different flow regimes and fluid properties?
The Flat Plate Heat Transfer Convected Equation and Calculator is capable of accounting for various flow regimes, including laminar and turbulent flows, as well as different fluid properties, such as viscosity, Prandtl number, and Reynolds number. The calculator uses empirical correlations and dimensionless numbers to predict the convective heat transfer coefficient, taking into account the characteristic length of the plate, the fluid velocity, and the temperature difference between the plate and the fluid. The calculator also considers the surface roughness of the plate, which can significantly affect the heat transfer rate. By inputting the relevant parameters, users can obtain accurate calculations of the convective heat transfer coefficient for a wide range of applications, from low-speed flows to high-speed flows, and from gases to liquids.
What are the limitations and assumptions of the Flat Plate Heat Transfer Convected Equation and Calculator, and how can they be addressed?
The Flat Plate Heat Transfer Convected Equation and Calculator is based on several assumptions and simplifications, which can limit its accuracy and applicability in certain situations. For example, the equation assumes a uniform temperature distribution on the plate, a constant fluid velocity, and a two-dimensional flow. Additionally, the calculator uses empirical correlations that are valid only for certain ranges of Reynolds numbers and Prandtl numbers. To address these limitations, users can employ numerical methods, such as computational fluid dynamics (CFD), to simulate the heat transfer and fluid flow more accurately. Furthermore, experimental validation can be used to verify the results obtained from the calculator, ensuring that the assumptions and simplifications are reasonable and the results are reliable.
How can the Flat Plate Heat Transfer Convected Equation and Calculator be used in conjunction with other heat transfer equations and calculators to solve complex heat transfer problems?
The Flat Plate Heat Transfer Convected Equation and Calculator can be used in conjunction with other heat transfer equations and calculators to solve complex heat transfer problems. For example, the calculator can be used to determine the convective heat transfer coefficient for a flat plate, while other equations and calculators can be used to calculate the conductive heat transfer through the plate, the radiative heat transfer from the plate, and the overall heat transfer rate. By combining these calculators and equations, users can solve complex heat transfer problems involving multiple modes of heat transfer, non-uniform temperature distributions, and complex geometries. Additionally, the calculator can be used to validate numerical simulations, such as CFD, and to provide initial conditions and boundary conditions for more complex heat transfer simulations. By using the Flat Plate Heat Transfer Convected Equation and Calculator in conjunction with other heat transfer tools, users can tackle a wide range of heat transfer problems and design more efficient and effective heat transfer systems.
Deja una respuesta

Entradas Relacionadas