Churchill Friction Factor Formulae and Calculator
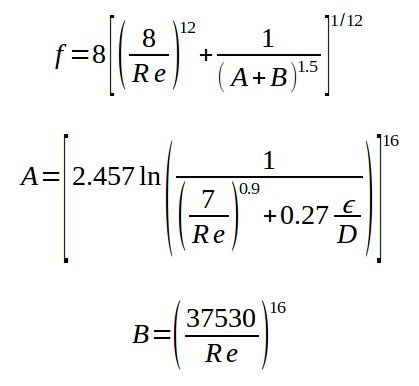
The Churchill friction factor formulae are widely used to calculate the friction factor in turbulent flow in pipes. These formulae provide a accurate estimate of the friction factor, which is essential in designing and optimizing piping systems. The formulae take into account the Reynolds number and the relative roughness of the pipe to determine the friction factor. With the help of a calculator, engineers can easily apply these formulae to determine the friction factor and design efficient piping systems. This article provides an overview of the Churchill friction factor formulae and a calculator to simplify the calculation process.
- Churchill Friction Factor Formulae and Calculator: A Comprehensive Guide
- What is the Churchill formula for friction factor?
- How do you calculate the friction factor?
- What is the formula for the friction factor of a pipe flow?
-
Frequently Asked Questions (FAQs)
- What is the Churchill Friction Factor Formulae and Calculator?
- How does the Churchill Friction Factor Formulae and Calculator work?
- What are the applications of the Churchill Friction Factor Formulae and Calculator?
- What are the limitations and uncertainties of the Churchill Friction Factor Formulae and Calculator?
Churchill Friction Factor Formulae and Calculator: A Comprehensive Guide
The Churchill friction factor formulae and calculator are essential tools in the field of fluid mechanics, particularly in the calculation of friction losses in pipes. The friction factor is a dimensionless quantity that represents the ratio of the shear stress at the wall of a pipe to the average velocity of the fluid flow. The Churchill formula is a widely used equation for calculating the friction factor in both laminar and turbulent flows.
Introduction to Churchill Friction Factor Formulae
The Churchill friction factor formulae are a set of equations that can be used to calculate the friction factor in pipes for a wide range of Reynolds numbers. The formulae take into account the roughness of the pipe wall and the viscosity of the fluid. The Churchill formula is a combination of the Colebrook-White equation and the Blasius equation, and it provides a more accurate calculation of the friction factor than other formulae.
Calculation of Friction Factor using Churchill Formulae
The Churchill formula for calculating the friction factor is as follows:
f = 8 [ (1/Re)^1/2 + (ε/3.7D)^1.11 ]^1/3
where f is the friction factor, Re is the Reynolds number, ε is the roughness of the pipe wall, and D is the diameter of the pipe. The formula can be used for both laminar and turbulent flows, and it provides a accurate calculation of the friction factor.
Comparison of Churchill Friction Factor Formulae with Other Formulae
The Churchill friction factor formulae are compared with other formulae, such as the Colebrook-White equation and the Blasius equation. The comparison shows that the Churchill formula provides a more accurate calculation of the friction factor than other formulae, especially for turbulent flows.
| Formula | Equation | Range of Application |
|---|---|---|
| Churchill | f = 8 [ (1/Re)^1/2 + (ε/3.7D)^1.11 ]^1/3 | Laminar and turbulent flows |
| Colebrook-White | 1/√f = -2log10(ε/3.7D + 2.51/Re√f) | Turbulent flows |
| Blasius | f = 0.316/Re^0.25 | Turbulent flows |
Churchill Friction Factor Calculator: An Overview
The Churchill friction factor calculator is a tool that can be used to calculate the friction factor in pipes using the Churchill formula. The calculator takes into account the Reynolds number, roughness of the pipe wall, and diameter of the pipe, and provides a accurate calculation of the friction factor. The calculator can be used for both laminar and turbulent flows, and it provides a range of options for fluid properties and pipe characteristics.
Applications of Churchill Friction Factor Formulae and Calculator
The Churchill friction factor formulae and calculator have a wide range of applications in the field of fluid mechanics, including the design of pipes, pumps, and turbines. The formulae and calculator can be used to calculate the friction losses in pipes, which is essential for determining the pressure drop and flow rate in a pipe system. The formulae and calculator can also be used to optimize the design of pipe systems, reducing energy losses and increasing efficiency. The friction factor is a critical parameter in the design of pipe systems, and the Churchill formulae and calculator provide a accurate and reliable method for calculating this parameter.
What is the Churchill formula for friction factor?

The Churchill formula for friction factor is a mathematical equation used to calculate the Darcy friction factor for fluid flow in pipes. The formula is given by:
1 / f^0.5 = -2log10(ε / 3.7Dh + 2.51 / Ref^0.5), where f is the Darcy friction factor, ε is the roughness of the pipe, Dh is the hydraulic diameter of the pipe, and Re is the Reynolds number. This formula is widely used in various fields, including chemical engineering, mechanical engineering, and civil engineering, to predict the pressure drop and flow rate in pipes.
Introduction to Friction Factor
The friction factor is a dimensionless quantity that represents the resistance to fluid flow in a pipe. It is an important parameter in the design and analysis of pipelines, as it affects the pressure drop and flow rate. The Churchill formula is a semi-empirical equation that combines the effects of turbulence and roughness on the friction factor. The formula is applicable to a wide range of flow conditions, from laminar to turbulent flow, and can be used for pipes of different materials and geometries.
- The Churchill formula is a widely used equation for calculating the friction factor.
- The formula takes into account the effects of turbulence and roughness on the friction factor.
- The formula is applicable to a wide range of flow conditions, from laminar to turbulent flow.
Applications of the Churchill Formula
The Churchill formula has numerous applications in various fields, including petroleum engineering, aerospace engineering, and environmental engineering. It is used to design and optimize pipelines, heat exchangers, and other fluid flow systems. The formula is also used to predict the pressure drop and flow rate in pipes, which is essential for the safe and efficient operation of these systems.
- The Churchill formula is used to!design and optimize pipelines.
- The formula is used to predict the pressure drop and flow rate in pipes.
- The formula is essential for the safe and efficient operation of fluid flow systems.
Limitations of the Churchill Formula
While the Churchill formula is widely used and accurate for many applications, it has some limitations. The formula is based on empirical correlations and may not be applicable to all flow conditions or pipe geometries. Additionally, the formula requires an iterative solution, which can be time-consuming and computationally intensive.
- The Churchill formula has limitations and may not be applicable to all flow conditions.
- The formula requires an iterative solution, which can be time-consuming and computationally intensive.
- The formula is based on empirical correlations and may not be accurate for all pipe geometries.
Comparison with Other Friction Factor Equations
The Churchill formula is one of several equations used to calculate the friction factor. Other notable equations include the Colebrook-White equation and the Haaland equation. Each equation has its own strengths and weaknesses, and the choice of equation depends on the specific application and flow conditions.
- The Churchill formula is one of several equations used to calculate the friction factor.
- Other notable equations include the Colebrook-White equation and the Haaland equation.
- Each equation has its own strengths and weaknesses, and the choice of equation depends on the specific application and flow conditions.
Implementation of the Churchill Formula in Computational Fluid Dynamics
The Churchill formula is widely used in computational fluid dynamics (CFD) to simulate fluid flow in pipes and other systems. The formula is implemented in various CFD software packages, including OpenFOAM and NetFLOW. The implementation of the Churchill formula in CFD allows for the accurate prediction of pressure drop and flow rate in complex fluid flow systems.
- The Churchill formula is widely used in computational fluid dynamics to simulate fluid flow in pipes and other systems.
- The formula is implemented in various CFD software packages, including OpenFOAM and NetFLOW.
- The implementation of the Churchill formula in CFD allows for the accurate prediction of pressure drop and flow rate in complex fluid flow systems.
How do you calculate the friction factor?
The friction factor is a dimensionless quantity used to calculate the frictional losses in a pipe flow. It is calculated using the Darcy-Weisbach equation, which relates the pressure drop to the flow rate, pipe diameter, and friction factor. The equation is given by: ΔP = (f L ρ v^2) / (2 D), where ΔP is the pressure drop, f is the friction factor, L is the pipe length, ρ is the fluid density, v is the flow velocity, and D is the pipe diameter.
Introduction to Friction Factor
The friction factor is an empirical value that depends on the Reynolds number, pipe roughness, and flow regime. It is used to calculate the head loss in a pipe, which is the loss of energy due to friction. The friction factor can be calculated using various equations and charts, such as the Colebrook-White equation and the Moody chart. The calculation involves the following steps:
- Calculate the Reynolds number using the formula: Re = ρ v D / μ, where ρ is the fluid density, v is the flow velocity, D is the pipe diameter, and μ is the fluid viscosity.
- Determine the pipe roughness and flow regime to select the appropriate equation or chart.
- Use the selected equation or chart to calculate the friction factor.
Methods for Calculating Friction Factor
There are several methods for calculating the friction factor, including the Colebrook-White equation, Moody chart, and Haaland equation. Each method has its own advantages and disadvantages, and the choice of method depends on the specific application and available data. The methods involve the following steps:
- Choose a method based on the available data and desired accuracy.
- Calculate the Reynolds number and pipe roughness.
- Use the selected method to calculate the friction factor.
Factors Affecting Friction Factor
The friction factor is affected by several factors, including the Reynolds number, pipe roughness, and flow regime. The Reynolds number is a dimensionless quantity that characterizes the flow regime, and it is used to determine the friction factor. The pipe roughness also affects the friction factor, as it increases the turbulence and frictional losses. The factors affecting the friction factor include:
- Reynolds number: affects the flow regime and friction factor.
- Pipe roughness: affects the turbulence and frictional losses.
- Flow regime: affects the friction factor and head loss.
Applications of Friction Factor
The friction factor has several applications in engineering and science, including the design of pipe networks, pumps, and turbines. It is used to calculate the head loss and pressure drop in a pipe, which is essential for designing efficient and cost-effective systems. The applications of the friction factor include:
- Pipe network design: to calculate the head loss and pressure drop.
- Pump design: to calculate the required pump power and head.
- Turbine design: to calculate the available energy and efficiency.
Limitations and Challenges
The calculation of the friction factor has several limitations and challenges, including the complexity of the equations and charts, and the uncertainty of the input data. The limitations and challenges include:
- Complexity: of the equations and charts used to calculate the friction factor.
- Uncertainty: of the input data, such as the pipe roughness and fluid viscosity.
- Sensitivity: of the friction factor to small changes in the input data.
What is the formula for the friction factor of a pipe flow?

The formula for the friction factor of a pipe flow is given by the Darcy-Weisbach equation, which is a widely used equation in the field of fluid dynamics. The equation is expressed as: f = (1 / (2 log10 (ε / 3.7 D + 2.51 / (Re √f)))^2), where f is the friction factor, ε is the roughness height, D is the pipe diameter, and Re is the Reynolds number.
Introduction to Friction Factor
The friction factor is a dimensionless quantity that is used to calculate the head loss in a pipe flow. It is an important parameter in the design of pipeline systems, as it helps to determine the pressure drop and the flow rate. The friction factor depends on the Reynolds number and the roughness height of the pipe. Here are some key points about the friction factor:
- The friction factor is a function of the Reynolds number, which is a measure of the ratio of inertial forces to viscous forces.
- The friction factor is also dependent on the roughness height of the pipe, which is a measure of the surface roughness.
- The friction factor is used to calculate the head loss in a pipe flow, which is an important consideration in the design of pipeline systems.
Types of Friction Factor
There are two main types of friction factor: the Darcy-Weisbach friction factor and the Colebrook-White friction factor. The Darcy-Weisbach friction factor is used for laminar flow, while the Colebrook-White friction factor is used for turbulent flow. Here are some key points about the types of friction factor:
- The Darcy-Weisbach friction factor is used for laminar flow, where the Reynolds number is less than 2000.
- The Colebrook-White friction factor is used for turbulent flow, where the Reynolds number is greater than 4000.
- The friction factor is also dependent on the pipe material and the fluid properties.
Applications of Friction Factor
The friction factor has a wide range of applications in the field of fluid dynamics. It is used to design pipeline systems, hydraulic systems, and pump systems. Here are some key points about the applications of friction factor:
- The friction factor is used to calculate the head loss in a pipe flow, which is an important consideration in the design of pipeline systems.
- The friction factor is used to determine the flow rate and pressure drop in a pipe flow.
- The friction factor is also used to design hydraulic systems, such as hydraulic pumps and hydraulic turbines.
Calculation of Friction Factor
The friction factor can be calculated using the Darcy-Weisbach equation or the Colebrook-White equation. The calculation involves the use of iterative methods, such as the Bisection method or the Newton-Raphson method. Here are some key points about the calculation of friction factor:
- The Darcy-Weisbach equation is used to calculate the friction factor for laminar flow.
- The Colebrook-White equation is used to calculate the friction factor for turbulent flow.
- The calculation of friction factor involves the use of iterative methods, such as the Bisection method or the Newton-Raphson method.
Importance of Friction Factor
The friction factor is an important parameter in the design of pipeline systems, hydraulic systems, and pump systems. It is used to calculate the head loss and pressure drop in a pipe flow, which is critical in determining the flow rate and efficiency of the system. Here are some key points about the importance of friction factor:
- The friction factor is used to calculate the head loss in a pipe flow, which is an important consideration in the design of pipeline systems.
- The friction factor is used to determine the flow rate and pressure drop in a pipe flow.
- The friction factor is also used to optimize the design of hydraulic systems and pump systems.
Frequently Asked Questions (FAQs)
What is the Churchill Friction Factor Formulae and Calculator?
The Churchill Friction Factor Formulae and Calculator is a mathematical model used to calculate the friction factor in pipe flow. This formula is widely used in engineering and physics to determine the pressure drop and flow rate in pipes. The Churchill Friction Factor Formulae is a semi-empirical equation that combines the laminar and turbulent flow regimes, making it a robust and reliable tool for engineering applications. The calculator is a software tool that implements this formula and allows users to input the necessary parameters, such as pipe diameter, flow rate, and fluid properties, to obtain the friction factor and other relevant quantities.
How does the Churchill Friction Factor Formulae and Calculator work?
The Churchill Friction Factor Formulae and Calculator works by solving the equation that relates the friction factor to the Reynolds number, pipe roughness, and other parameters. The formula is based on a semi-empirical approach that combines the laminar and turbulent flow regimes, using curve-fitting techniques to match the experimental data. The calculator takes the input parameters and solves the equation using numerical methods, such as iteration or optimization techniques, to obtain the friction factor and other relevant quantities. The calculator also provides a graphical interface to visualize the results and explore the parameter space, allowing users to investigate the effects of different parameters on the friction factor.
What are the applications of the Churchill Friction Factor Formulae and Calculator?
The Churchill Friction Factor Formulae and Calculator has a wide range of applications in engineering and physics, including pipe flow, fluid mechanics, and heat transfer. The formula and calculator are used to design and optimize pipe systems, such as water supply and gas transmission lines, as well as chemical processing and power generation plants. The calculator is also used to analyze and predict the behavior of complex systems, such as networks of pipes and channels, and to investigate the effects of roughness, corrosion, and other factors on the friction factor. Additionally, the Churchill Friction Factor Formulae is used in research and development to study the fundamentals of pipe flow and to improve the accuracy and reliability of engineering models.
What are the limitations and uncertainties of the Churchill Friction Factor Formulae and Calculator?
The Churchill Friction Factor Formulae and Calculator, like any mathematical model, has limitations and uncertainties that must be considered when applying it to real-world problems. The formula is based on simplifying assumptions, such as steady-state and fully-developed flow, which may not always be valid in practice. Additionally, the calculator relies on numerical methods that may introduce errors and uncertainties, particularly when dealing with complex or nonlinear problems. Furthermore, the Churchill Friction Factor Formulae is a semi-empirical approach that is calibrated using experimental data, which may not always be available or reliable. Therefore, users must be aware of these limitations and uncertainties and use the calculator with caution, validating the results whenever possible using experimental data or other methods.
Deja una respuesta

Entradas Relacionadas