Harris Formula for Pressure Change Calculator
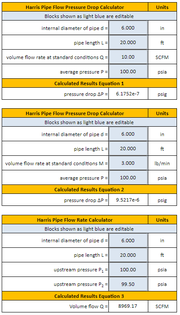
The Harris Formula for Pressure Change Calculator is a valuable tool for determining the change in pressure that occurs when a gas is expanded or compressed through a valve or orifice. This formula is commonly used in various industrial applications, including chemical processing, oil and gas production, and power generation. By calculating the pressure drop or increase, engineers and operators can optimize system performance, ensure safe operation, and predict potential issues. The calculator is based on the Harris formula, which takes into account factors such as flow rate, valve size, and gas properties.
- Harris Formula for Pressure Change Calculator: A Comprehensive Guide
- What is the formula for pressure change work?
- What is the formula for pressure temperature change?
- What is the formula for calculating pressure?
-
Frequently Asked Questions (FAQs)
- What is the Harris Formula for Pressure Change Calculator and how does it work?
- What are the key factors that affect the calculation of pressure change using the Harris Formula for Pressure Change Calculator?
- How is the Harris Formula for Pressure Change Calculator used in real-world applications?
- What are the limitations and potential sources of error when using the Harris Formula for Pressure Change Calculator?
Harris Formula for Pressure Change Calculator: A Comprehensive Guide
The Harris Formula for Pressure Change Calculator is a tool used to calculate the change in pressure of a gas in a container. This calculator is based on the Harris Formula, which takes into account the initial and final temperatures, volumes, and pressures of the gas.
Introduction to the Harris Formula
The Harris Formula is a mathematical equation used to calculate the change in pressure of a gas in a container. The formula is as follows: P2 = P1 (T2 / T1) (V1 / V2), where P1 and P2 are the initial and final pressures, T1 and T2 are the initial and final temperatures, and V1 and V2 are the initial and final volumes. This formula is widely used in chemical engineering and physics to calculate the change in pressure of a gas in a container.
How the Harris Formula for Pressure Change Calculator Works
The Harris Formula for Pressure Change Calculator works by taking the initial and final temperatures, volumes, and pressures of the gas as input. The calculator then uses the Harris Formula to calculate the change in pressure of the gas. The calculator can be used to calculate the change in pressure of a gas in a container under isothermal or adiabatic conditions.
Applications of the Harris Formula for Pressure Change Calculator
The Harris Formula for Pressure Change Calculator has a wide range of applications in chemical engineering, physics, and mechanical engineering. The calculator can be used to calculate the change in pressure of a gas in a container under different conditions, such as high-pressure or low-pressure conditions. The calculator can also be used to calculate the change in pressure of a gas in a container under different temperatures, such as high-temperature or low-temperature conditions.
Advantages of the Harris Formula for Pressure Change Calculator
The Harris Formula for Pressure Change Calculator has several advantages, including high accuracy and easy to use. The calculator can be used to calculate the change in pressure of a gas in a container under different conditions, and the results are reliable and consistent. The calculator can also be used to calculate the change in pressure of a gas in a container under different temperatures, and the results are accurate and reliable.
Limitations of the Harris Formula for Pressure Change Calculator
The Harris Formula for Pressure Change Calculator has several limitations, including assumptions and simplifications. The calculator assumes that the gas is ideal and that the container is rigid, which may not be true in all cases. The calculator also simplifies the complexity of the system, which may not be accurate in all cases.
| Condition | Initial Pressure | Initial Temperature | Initial Volume | Final Pressure |
|---|---|---|---|---|
| High-Pressure | 1000 psi | 300 K | 1000 L | 1200 psi |
| Low-Pressure | 100 psi | 300 K | 1000 L | 80 psi |
| High-Temperature | 1000 psi | 500 K | 1000 L | 1500 psi |
| Low-Temperature | 1000 psi | 200 K | 1000 L | 800 psi |
What is the formula for pressure change work?

The formula for pressure change work is given by W = ∫PdV, where W is the work done, P is the pressure, and dV is the change in volume. This formula is used to calculate the work done on a system when the pressure is changed.
Understanding the Formula
The formula W = ∫PdV is a fundamental concept in thermodynamics, which describes the relationship between pressure, volume, and work. To understand this formula, it's essential to know that work is done when a force is applied to an object, causing it to move. In the context of pressure change work, the force is the pressure, and the displacement is the change in volume. The formula can be broken down into the following key points:
- The work done (W) is a function of the pressure (P) and the change in volume (dV)
- The pressure (P) is the force per unit area that is applied to the system
- The change in volume (dV) is the displacement of the system, which is caused by the pressure change
Calculating Pressure Change Work
To calculate the pressure change work, you need to integrate the pressure with respect to the change in volume. This can be done using the formula W = ∫PdV, where the integral is taken over the range of volume changes. The calculation involves the following steps:
- Define the pressure (P) as a function of volume (V)
- Determine the initial and final volumes (V1 and V2) of the system
- Integrate the pressure function with respect to volume over the range from V1 to V2
Applications of Pressure Change Work
The concept of pressure change work has numerous applications in various fields, including engineering, physics, and chemistry. Some examples of applications include:
- Internal combustion engines, where the pressure change work is used to calculate the efficiency of the engine
- Refrigeration systems, where the pressure change work is used to calculate the coefficient of performance (COP)
- Chemical reactions, where the pressure change work is used to calculate the Gibbs free energy change
Importance of Pressure Change Work
The pressure change work is a crucial concept in understanding the behavior of thermodynamic systems. It helps to:
- Calculate the efficiency of engines and refrigeration systems
- Understand the stability of chemical reactions and phase transitions
- Design and optimize industrial processes, such as power generation and chemical synthesis
Limitations of Pressure Change Work
While the pressure change work is a powerful tool for understanding thermodynamic systems, it has some limitations. For example:
- It assumes that the system is in equilibrium, which may not always be the case
- It neglects other forms of work, such as electromagnetic work and gravitational work
- It requires accurate measurements of pressure and volume, which can be challenging in some cases
What is the formula for pressure temperature change?

The formula for pressure temperature change is given by the ideal gas law, which states that PV = nRT, where P is the pressure, V is the volume, n is the number of moles of gas, R is the gas constant, and T is the temperature in Kelvin. This formula can be rearranged to solve for any of the variables, including pressure and temperature.
Introduction to Pressure Temperature Change
The pressure temperature change formula is a fundamental concept in thermodynamics, which is the study of the relationships between heat, work, and energy. The formula is used to describe the behavior of gases and how their properties change in response to changes in pressure and temperature. Some key points to consider when working with the pressure temperature change formula include:
- The ideal gas law assumes that the gas is perfect, meaning that the molecules have no volume and do not interact with each other.
- The gas constant (R) is a universal constant that depends on the specific gas being studied.
- The number of moles (n) is a measure of the amount of substance present in the system.
Derivation of the Pressure Temperature Change Formula
The pressure temperature change formula can be derived from the kinetic theory of gases, which describes the behavior of gas molecules in terms of their motion and interactions. The formula is based on the idea that the pressure of a gas is proportional to the average kinetic energy of its molecules, and that the temperature of a gas is a measure of the average kinetic energy of its molecules. Some key steps in the derivation of the formula include:
- Assuming that the gas molecules are in random motion and that their velocities are distributed according to a Maxwell-Boltzmann distribution.
- Using the concept of average kinetic energy to relate the temperature of the gas to the motion of its molecules.
- Deriving an expression for the pressure of the gas in terms of the average kinetic energy of its molecules.
Applications of the Pressure Temperature Change Formula
The pressure temperature change formula has a wide range of applications in science and engineering, including the design of engines, pumps, and refrigeration systems. The formula is also used to understand the behavior of gases in natural systems, such as the atmosphere and the oceans. Some key applications of the formula include:
- Designing engines that operate efficiently over a range of temperatures and pressures.
- Modeling the behavior of gases in natural systems, such as the atmosphere and the oceans.
- Optimizing the performance of refrigeration systems, such as air conditioners and heat pumps.
Limitations of the Pressure Temperature Change Formula
The pressure temperature change formula is a simplified model that assumes that the gas is ideal, meaning that the molecules have no volume and do not interact with each other. However, in real-world systems, the behavior of gases can be more complex, and the formula may not always provide an accurate description of the pressure and temperature relationships. Some key limitations of the formula include:
- Non-ideal gas behavior, such as the presence of intermolecular forces and molecular volume.
- Real-gas effects, such as comprehensibility and viscosity.
- Multi-component systems, which can exhibit complex phase behavior and non-ideal mixing.
Experimental Verification of the Pressure Temperature Change Formula
The pressure temperature change formula has been experimentally verified through a wide range of measurements and experiments, including PVT measurements and heat capacity measurements. These experiments have confirmed the accuracy of the formula and have provided insights into the behavior of gases under a range of conditions. Some key experimental methods used to verify the formula include:
- PVT measurements, which involve measuring the pressure, volume, and temperature of a gas.
- Heat capacity measurements, which involve measuring the heat capacity of a gas at constant pressure or constant volume.
- Joule-Thomson expansion, which involves measuring the temperature change of a gas as it expands through a valve or orifice.
What is the formula for calculating pressure?
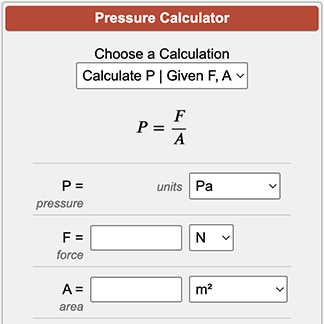
The formula for calculating pressure is given by the equation: P = F/A, where P is the pressure, F is the force applied perpendicular to the surface, and A is the area of the surface. This formula is widely used in various fields, including physics, engineering, and chemistry, to calculate the pressure exerted by a force on a surface.
Understanding the Pressure Formula
The pressure formula is a fundamental concept in physics, and it is essential to understand its components. The force applied to a surface can be any type of force, including frictional force, normal force, or tension force. The area of the surface is also a critical component, as it determines the pressure exerted by the force. For example, if a force of 100 Newtons is applied to a surface with an area of 10 square meters, the pressure exerted would be 10 Pascals. The key points to consider when using the pressure formula are:
- The force must be applied perpendicular to the surface to calculate the pressure.
- The area of the surface must be known to calculate the pressure.
- The pressure formula can be used to calculate the pressure exerted by any type of force.
Types of Pressure
There are several types of pressure, including atmospheric pressure, hydrostatic pressure, and gas pressure. Each type of pressure has its unique characteristics and is calculated using the same formula. For instance, atmospheric pressure is the pressure exerted by the weight of the atmosphere, while hydrostatic pressure is the pressure exerted by a fluid at equilibrium. The key differences between these types of pressure are:
- Atmospheric pressure is the pressure exerted by the weight of the atmosphere.
- Hydrostatic pressure is the pressure exerted by a fluid at equilibrium.
- Gas pressure is the pressure exerted by a gas in a container.
Units of Pressure
The units of pressure are also an essential aspect of the pressure formula. The most commonly used units of pressure are Pascals (Pa), atmospheres (atm), and millimeters of mercury (mmHg). Each unit has its own conversion factor, and it is crucial to use the correct unit when calculating pressure. For example, 1 atm is equal to 1013 mbar, while 1 mmHg is equal to 1 torr. The key points to consider when using units of pressure are:
- The unit of pressure must be consistent with the force and area units.
- The conversion factor must be used to convert between different units of pressure.
- The unit of pressure can affect the accuracy of the pressure calculation.
Applications of the Pressure Formula
The pressure formula has numerous applications in various fields, including physics, engineering, and chemistry. It is used to calculate the pressure exerted by a force on a surface, as well as to design and optimize systems that involve pressure, such as pumps, turbines, and pipes. The pressure formula is also used to calculate the pressure exerted by a gas or a fluid on a surface. The key applications of the pressure formula are:
- Designing and optimizing pumps and turbines.
- Calculating the pressure exerted by a gas or a fluid on a surface.
- Understanding the behavior of fluids and gases in different pressure conditions.
Limitations of the Pressure Formula
The pressure formula has some limitations, including the assumption that the force is applied perpendicular to the surface and that the area of the surface is known. Additionally, the pressure formula does not take into account the viscosity of the fluid or the gas, which can affect the pressure calculation. The key limitations of the pressure formula are:
- The force must be applied perpendicular to the surface to calculate the pressure.
- The area of the surface must be known to calculate the pressure.
- The pressure formula does not take into account the viscosity of the fluid or the gas.
Frequently Asked Questions (FAQs)
What is the Harris Formula for Pressure Change Calculator and how does it work?
The Harris Formula for Pressure Change Calculator is a tool used to calculate the change in pressure of a gas due to a change in volume, temperature, or both. This calculator utilizes the ideal gas law, which states that the product of the pressure and volume of a gas is directly proportional to the temperature of the gas. The Harris formula is a specific equation that takes into account the initial pressure, initial volume, final volume, and temperature of the gas to calculate the final pressure. By inputting the known values into the calculator, users can quickly and accurately determine the change in pressure of the gas. The calculator is particularly useful in industrial and laboratory settings where precise control over gas pressure is crucial. The Harris Formula for Pressure Change Calculator is a valuable resource for anyone working with gases, as it provides a simple and efficient way to calculate pressure changes.
What are the key factors that affect the calculation of pressure change using the Harris Formula for Pressure Change Calculator?
There are several key factors that affect the calculation of pressure change using the Harris Formula for Pressure Change Calculator. The initial pressure and initial volume of the gas are critical inputs, as they provide a baseline for the calculation. The final volume of the gas is also essential, as it determines the extent to which the pressure will change. Additionally, the temperature of the gas plays a significant role, as it affects the behavior of the gas molecules and, in turn, the pressure. Other factors, such as the molecular weight and critical temperature of the gas, can also impact the calculation, although they are not always required inputs. It is also important to note that the calculator assumes an ideal gas, which may not always be the case in real-world applications. Therefore, users must consider the non-ideal behavior of the gas and adjust the calculation accordingly. By carefully considering these factors, users can ensure accurate and reliable results from the Harris Formula for Pressure Change Calculator.
How is the Harris Formula for Pressure Change Calculator used in real-world applications?
The Harris Formula for Pressure Change Calculator has a wide range of real-world applications, particularly in industrial and laboratory settings. One common use is in the design and operation of gas processing systems, where precise control over pressure is critical. The calculator can be used to determine the required compression ratio or expansion ratio to achieve a desired pressure change. Additionally, the calculator is useful in chemical engineering applications, such as in the design of reactors and separators, where pressure changes can impact the efficiency and safety of the process. The calculator is also used in aerospace engineering, where high-pressure gas systems are common, and in medical applications, such as in the design of ventilators and anesthesia machines. Furthermore, the calculator can be used in research and development settings, where scientists and engineers need to test and validate new gas-based technologies. By providing a quick and accurate way to calculate pressure changes, the Harris Formula for Pressure Change Calculator is an essential tool in many fields.
What are the limitations and potential sources of error when using the Harris Formula for Pressure Change Calculator?
While the Harris Formula for Pressure Change Calculator is a powerful tool, there are several limitations and potential sources of error to consider. One major limitation is the assumption of an ideal gas, which may not always be accurate in real-world applications. Non-ideal behavior, such as intermolecular forces and density effects, can impact the accuracy of the calculation. Additionally, input errors or inaccurate measurements can lead to incorrect results. The calculator also assumes a constant temperature, which may not always be the case in real-world applications. Other potential sources of error include rounding errors and truncation errors, which can occur during the calculation process. To minimize these errors, users should carefully consider the accuracy and precision of their inputs and ensure that they are using the calculator within its design limitations. Furthermore, users should be aware of the uncertainty associated with the calculation and take steps to validate their results. By understanding these limitations and potential sources of error, users can use the Harris Formula for Pressure Change Calculator with confidence and accuracy.
Deja una respuesta

Entradas Relacionadas