Contact Stress Sphere Calculator on Concave Surface including Formulas
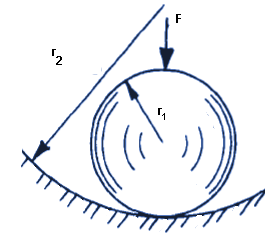
The Contact Stress Sphere Calculator is a valuable tool for determining the contact stress between a sphere and a concave surface. This calculator is essential in various engineering applications, including mechanical design, tribology, and materials science. By using the calculator, engineers can quickly and accurately determine the contact stress, which is critical in predicting the performance and lifespan of mechanical components. The calculator utilizes complex formulas to provide precise calculations, taking into account the radius of the sphere and the curvatures of the concave surface. These calculations are based on Hertzian contact theory.
- Contact Stress Sphere Calculator on Concave Surface including Formulas
-
Understanding the Contact Stress Sphere Calculator on Concave Surface including Formulas
- Introduction to Contact Stress and its Importance
- Formulas Used in the Contact Stress Sphere Calculator
- Assumptions and Limitations of the Contact Stress Sphere Calculator
- Applications of the Contact Stress Sphere Calculator
- Future Developments and Improvements of the Contact Stress Sphere Calculator
-
Frequently Asked Questions (FAQs)
- What is the Contact Stress Sphere Calculator on Concave Surface including Formulas and how does it work?
- What are the key parameters considered in the Contact Stress Sphere Calculator on Concave Surface including Formulas?
- How do the formulas used in the Contact Stress Sphere Calculator on Concave Surface including Formulas account for the elastic properties of the materials in contact?
- What are the limitations and assumptions of the Contact Stress Sphere Calculator on Concave Surface including Formulas, and how can they be addressed?
Contact Stress Sphere Calculator on Concave Surface including Formulas
The contact stress sphere calculator is a tool used to calculate the contact stress between a sphere and a concave surface. This calculator is particularly useful in engineering and physics applications where the stress and strain on materials are critical. The calculator takes into account the radius of the sphere, the radius of the concave surface, and the material properties of the sphere and the surface. The calculation involves the use of Hertzian contact theory, which provides a mathematical model for the contact stress between two elastic spheres.
Introduction to Contact Stress Sphere Calculator
The contact stress sphere calculator is an essential tool in understanding the mechanics of contact between a sphere and a concave surface. The calculator uses formulas based on the Hertzian contact theory to calculate the contact stress and contact area between the sphere and the surface. The calculator is widely used in engineering design and research applications to predict the stress and strain on materials.
Formulas Used in Contact Stress Sphere Calculator
The contact stress sphere calculator uses several formulas to calculate the contact stress and contact area between the sphere and the concave surface. The formulas include:
| Formula | Description |
|---|---|
| Contact Stress Formula | Calculates the contact stress between the sphere and the surface |
| Contact Area Formula | Calculates the contact area between the sphere and the surface |
Key Factors Affecting Contact Stress Sphere Calculator
Several key factors affect the contact stress between a sphere and a concave surface. These factors include the radius of the sphere, the radius of the concave surface, and the material properties of the sphere and the surface. The friction coefficient between the sphere and the surface also plays a significant role in determining the contact stress.
Applications of Contact Stress Sphere Calculator
The contact stress sphere calculator has several applications in engineering design and research. The calculator is used to predict the stress and strain on materials in various applications, including mechanical engineering, civil engineering, and materials science. The calculator is also used to optimize the design of mechanical systems and structures.
Limitations of Contact Stress Sphere Calculator
The contact stress sphere calculator has several limitations. The calculator assumes that the sphere and the concave surface are elastic and isotropic, which may not always be the case. The calculator also assumes that the contact between the sphere and the surface is frictionless, which may not be realistic in all applications. These limitations must be considered when using the contact stress sphere calculator to predict the stress and strain on materials.
Understanding the Contact Stress Sphere Calculator on Concave Surface including Formulas
The Contact Stress Sphere Calculator on Concave Surface is a tool used to calculate the contact stress between a sphere and a concave surface. This calculator is particularly useful in various fields such as engineering, physics, and materials science. The calculator takes into account the radius of the sphere, the radius of curvature of the concave surface, and the applied load to determine the contact stress. The contact stress is an important factor in determining the wear and tear of the surfaces in contact, as well as the probability of failure due to fatigue or fracture.
Introduction to Contact Stress and its Importance
Contact stress refers to the normal stress that occurs at the point of contact between two surfaces. It is a critical parameter in evaluating the structural integrity of components and systems. High contact stress can lead to plastic deformation, cracking, or failure of the surfaces in contact. The Contact Stress Sphere Calculator on Concave Surface including Formulas is designed to provide accurate calculations of contact stress, taking into account the geometric and material properties of the sphere and the concave surface. The calculator uses formulas derived from the theory of elasticity and contact mechanics to determine the contact stress.
Formulas Used in the Contact Stress Sphere Calculator
The Contact Stress Sphere Calculator on Concave Surface uses several formulas to calculate the contact stress. The most commonly used formula is the Hertzian contact theory, which describes the contact between two elastic spheres. The formula takes into account the radius of the sphere, the radius of curvature of the concave surface, and the applied load. The calculator also uses modifications to the Hertzian contact theory to account for non-elastic behavior and friction. The formulas used in the calculator are based on the assumptions of linear elasticity and small deformations. The calculator also provides options for non-linear and large deformation cases, which require numerical methods to solve.
Assumptions and Limitations of the Contact Stress Sphere Calculator
The Contact Stress Sphere Calculator on Concave Surface including Formulas is based on several assumptions and limitations. The calculator assumes that the sphere and the concave surface are isotropic and homogeneous, and that the contact is frictionless. The calculator also assumes that the deformations are small and that the material behavior is elastic. However, in real-world applications, the materials may exhibit non-elastic behavior, and the contact may be subject to friction. The calculator provides options to account for these non-ideal cases, but the accuracy of the calculations may be affected. The calculator is also limited to spherical and concave surfaces, and may not be applicable to other geometries.
Applications of the Contact Stress Sphere Calculator
The Contact Stress Sphere Calculator on Concave Surface including Formulas has numerous applications in various fields such as engineering, physics, and materials science. The calculator can be used to design and optimize components and systems, such as bearings, gears, and cams. The calculator can also be used to evaluate the structural integrity of existing systems and to predict the probability of failure due to fatigue or fracture. The calculator is particularly useful in high-cycle fatigue applications, where the contact stress is a critical parameter in determining the life of the component.
Future Developments and Improvements of the Contact Stress Sphere Calculator
The Contact Stress Sphere Calculator on Concave Surface including Formulas is a continuously evolving tool, with new developments and improvements being made regularly. Researchers and developers are working to enhance the accuracy and reliability of the calculator, and to expand its capabilities to include other geometries and material properties. The calculator is also being integrated with other tools and software, such as finite element analysis and computational fluid dynamics, to provide a more comprehensive and integrated design and analysis environment. The future developments of the calculator will focus on improving the user interface, increasing the speed and efficiency of the calculations, and expanding the range of applications.
Frequently Asked Questions (FAQs)
What is the Contact Stress Sphere Calculator on Concave Surface including Formulas and how does it work?
The Contact Stress Sphere Calculator is a tool used to calculate the stress between a sphere and a concave surface. This calculator is particularly useful in engineering and physics applications where the contact stress between two surfaces is critical. The calculator takes into account the radius of the sphere, the radius of curvature of the concave surface, and the elastic properties of the materials in contact. By using formulas derived from the Hertzian contact theory, the calculator can determine the contact stress, contact area, and deformation of the sphere and the concave surface. The formulas used in the calculator are based on the principles of elasticity and contact mechanics, allowing for accurate calculations of the contact stress and other relevant parameters.
What are the key parameters considered in the Contact Stress Sphere Calculator on Concave Surface including Formulas?
The Contact Stress Sphere Calculator considers several key parameters to calculate the contact stress between a sphere and a concave surface. The radius of the sphere is a critical parameter, as it affects the contact area and the stress distribution between the two surfaces. The radius of curvature of the concave surface is also an important parameter, as it influences the contact stress and the deformation of the sphere and the concave surface. Additionally, the elastic properties of the materials in contact, such as the Young's modulus and Poisson's ratio, are taken into account to determine the contact stress and deformation. The normal load applied to the sphere and the concave surface is also a key parameter, as it affects the contact stress and the contact area. By considering these parameters, the calculator can provide accurate calculations of the contact stress and other relevant parameters.
How do the formulas used in the Contact Stress Sphere Calculator on Concave Surface including Formulas account for the elastic properties of the materials in contact?
The formulas used in the Contact Stress Sphere Calculator account for the elastic properties of the materials in contact by incorporating the Young's modulus and Poisson's ratio of the materials. The Hertzian contact theory is used to derive the formulas for the contact stress and deformation of the sphere and the concave surface. The Young's modulus is a measure of the stiffness of the material, while the Poisson's ratio is a measure of the lateral strain response of the material to a normal load. By incorporating these elastic properties into the formulas, the calculator can accurately predict the contact stress and deformation of the sphere and the concave surface, taking into account the elastic behavior of the materials in contact. The formulas used in the calculator are based on the assumption that the materials in contact are isotropic and homogeneous, and that the contact stress is static and axisymmetric.
What are the limitations and assumptions of the Contact Stress Sphere Calculator on Concave Surface including Formulas, and how can they be addressed?
The Contact Stress Sphere Calculator has several limitations and assumptions that should be considered when using the calculator. One of the main limitations is that the calculator assumes that the materials in contact are isotropic and homogeneous, which may not be the case in real-world applications. Additionally, the calculator assumes that the contact stress is static and axisymmetric, which may not be true in situations where the contact stress is dynamic or asymmetric. To address these limitations, more advanced models and simulations can be used, such as finite element analysis or computational fluid dynamics. Furthermore, the calculator assumes that the radius of curvature of the concave surface is constant, which may not be the case in situations where the radius of curvature varies along the surface. To address this limitation, more sophisticated models can be used, such as non-uniform radius of curvature models. By understanding the limitations and assumptions of the calculator, users can ensure that the results are accurate and reliable for their specific application.
Deja una respuesta

Entradas Relacionadas