Convective Heat Transfer Convection Equation and Calculator

Convective heat transfer is a crucial process in various industries, including engineering, chemistry, and physics. It occurs when a fluid, such as air or water, comes into contact with a surface at a different temperature, resulting in heat transfer. The convection equation is used to calculate the rate of heat transfer due to convection, taking into account factors like temperature difference, fluid velocity, and surface area. This article will delve into the convection equation and provide a calculator to simplify the process of determining convective heat transfer rates in various applications. Accurate calculations are essential for design and optimization.
- Convective Heat Transfer: Understanding the Convection Equation and Calculator
- How do you calculate convection heat transfer?
- What is the equation for heat convection?
- How do you calculate the heat transmission by convection?
- What is the formula for calculating heat transfer?
- Frequently Asked Questions (FAQs)
Convective Heat Transfer: Understanding the Convection Equation and Calculator
Convective heat transfer is a fundamental concept in thermodynamics, which involves the transfer of heat between a solid surface and a fluid (liquid or gas) in motion. This process is crucial in various engineering applications, including heat exchangers, electronic cooling systems, and HVAC systems. The convective heat transfer coefficient (h) is a key parameter in determining the rate of heat transfer between the surface and the fluid. The convection equation, also known as Newton's law of cooling, is used to calculate the convective heat transfer coefficient.
Introduction to Convective Heat Transfer
Convective heat transfer occurs when there is a temperature difference between a solid surface and a fluid in motion. The fluid can be a liquid or a gas, and the motion can be natural (free convection) or forced (forced convection). The convective heat transfer coefficient (h) depends on various factors, including the fluid properties, flow velocity, and surface roughness. Understanding the fundamentals of convective heat transfer is essential for designing efficient heat transfer systems.
Convection Equation and Calculator
The convection equation is given by:
Q = h A (T_s - T_f)
where Q is the heat transfer rate, h is the convective heat transfer coefficient, A is the surface area, T_s is the surface temperature, and T_f is the fluid temperature. The convective heat transfer coefficient (h) can be calculated using various correlations, such as the Nusselt number (Nu) and the Reynolds number (Re). A convective heat transfer calculator can be used to determine the convective heat transfer coefficient and heat transfer rate for a given set of conditions.
Factors Affecting Convective Heat Transfer
Several factors affect the convective heat transfer coefficient, including:
| Factor | Description |
|---|---|
| Fluid properties | The fluid's density, viscosity, and thermal conductivity affect the convective heat transfer coefficient. |
| Flow velocity | The flow velocity of the fluid affects the convective heat transfer coefficient, with higher velocities resulting in higher heat transfer rates. |
| Surface roughness | The surface roughness of the solid surface affects the convective heat transfer coefficient, with rougher surfaces resulting in higher heat transfer rates. |
Applications of Convective Heat Transfer
Convective heat transfer has numerous applications in various fields, including:
the electronic cooling industry, where it is used to cool electronic devices such as computers and smartphones. The HVAC industry, where it is used to design heating, ventilation, and air conditioning systems. The automotive industry, where it is used to design cooling systems for vehicles. The aerospace industry, where it is used to design thermal management systems for spacecraft and aircraft.
Calculating Convective Heat Transfer Coefficient
The convective heat transfer coefficient (h) can be calculated using various correlations, such as the Dittus-Boelter equation and the Colburn equation. These correlations depend on the Reynolds number (Re) and the Prandtl number (Pr) of the fluid. A convective heat transfer calculator can be used to determine the convective heat transfer coefficient and heat transfer rate for a given set of conditions, including the fluid properties, flow velocity, and surface roughness.
How do you calculate convection heat transfer?
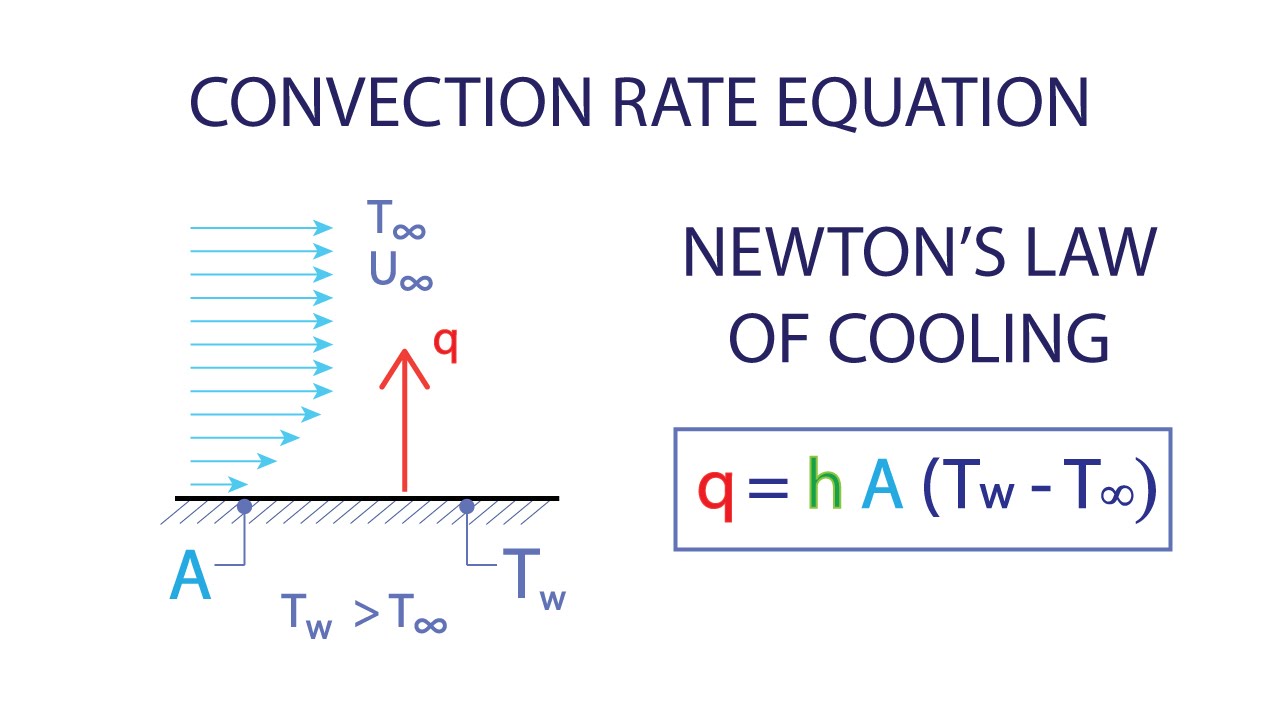
To calculate convection heat transfer, you need to understand the principles of fluid dynamics and heat transfer. Convection heat transfer occurs when a fluid (such as air or water) flows over a surface, causing heat to be transferred from the surface to the fluid. The calculation involves determining the convective heat transfer coefficient, which depends on the flow velocity, fluid properties, and surface roughness.
Introduction to Convection Heat Transfer
Convection heat transfer is a complex phenomenon that involves the movement of fluids and the transfer of thermal energy. To calculate convection heat transfer, you need to consider the Reynolds number, which determines whether the flow is laminar or turbulent. The calculation also involves determining the Prandtl number, which characterizes the thermal conductivity and viscosity of the fluid. Some key points to consider when calculating convection heat transfer include:
- Flow velocity: The velocity of the fluid flowing over the surface affects the convective heat transfer coefficient.
- Fluid properties: The density, viscosity, and thermal conductivity of the fluid affect the convective heat transfer coefficient.
- Surface roughness: The roughness of the surface affects the convective heat transfer coefficient, with rougher surfaces resulting in higher heat transfer rates.
Convective Heat Transfer Coefficient
The convective heat transfer coefficient (h) is a critical parameter in calculating convection heat transfer. It depends on the flow velocity, fluid properties, and surface roughness. To calculate the convective heat transfer coefficient, you can use empirical correlations or numerical models. Some key points to consider when calculating the convective heat transfer coefficient include:
- Nusselt number: The Nusselt number (Nu) is a dimensionless parameter that characterizes the convective heat transfer coefficient.
- Reynolds number: The Reynolds number (Re) determines whether the flow is laminar or turbulent.
- Prandtl number: The Prandtl number (Pr) characterizes the thermal conductivity and viscosity of the fluid.
Forced Convection Heat Transfer
Forced convection heat transfer occurs when a fluid is forced to flow over a surface using a pump or fan. To calculate forced convection heat transfer, you need to consider the flow velocity, fluid properties, and surface roughness. Some key points to consider when calculating forced convection heat transfer include:
- Flow rate: The flow rate of the fluid affects the convective heat transfer coefficient.
- Pump power: The pump power required to force the fluid to flow affects the overall energy balance.
- Heat exchanger design: The design of the heat exchanger affects the convective heat transfer coefficient and the overall heat transfer rate.
Natural Convection Heat Transfer
Natural convection heat transfer occurs when a fluid flows over a surface due to buoyancy. To calculate natural convection heat transfer, you need to consider the temperature difference, fluid properties, and surface roughness. Some key points to consider when calculating natural convection heat transfer include:
- Temperature difference: The temperature difference between the surface and the fluid affects the convective heat transfer coefficient.
- Grashof number: The Grashof number (Gr) characterizes the buoyancy force driving the fluid flow.
- Rayleigh number: The Rayleigh number (Ra) characterizes the heat transfer rate in natural convection.
Applications of Convection Heat Transfer
Convection heat transfer has numerous applications in engineering and science, including heat exchangers, cooling systems, and thermal management. To calculate convection heat transfer in these applications, you need to consider the specific requirements and constraints of each system. Some key points to consider when calculating convection heat transfer in applications include:
- System design: The design of the system affects the convective heat transfer coefficient and the overall heat transfer rate.
- Material selection: The selection of materials affects the thermal conductivity and viscosity of the fluid.
- Operating conditions: The operating conditions, such as temperature and pressure, affect the convective heat transfer coefficient and the overall heat transfer rate.
What is the equation for heat convection?

The equation for heat convection is given by the convective heat transfer coefficient equation, which is represented as: Q = h A (T1 - T2), where Q is the heat transfer rate, h is the convective heat transfer coefficient, A is the surface area, and T1 and T2 are the temperatures of the two objects or fluids.
Introduction to Convective Heat Transfer
Convective heat transfer is the process by which heat energy is transferred between a solid surface and a surrounding fluid, such as air or water. This process occurs through the motion of fluid molecules, which carry heat away from the surface. The equation for convective heat transfer is used to determine the rate of heat transfer between the surface and the surrounding fluid. Some key factors that influence convective heat transfer include:
- Surface roughness: A rough surface can increase the turbulence of the fluid, leading to increased heat transfer.
- Fluid velocity: Increasing the velocity of the fluid can enhance heat transfer by increasing the convection currents.
- Temperature difference: A larger temperature difference between the surface and the fluid can increase the heat transfer rate.
Factors Affecting Convective Heat Transfer Coefficient
The convective heat transfer coefficient (h) is a critical parameter in the equation for convective heat transfer. It depends on several factors, including the fluid properties, such as density, viscosity, and thermal conductivity, as well as the surface geometry and fluid velocity. The convective heat transfer coefficient can be calculated using correlations or empirical equations, which take into account the specific conditions of the system. Some key factors that affect the convective heat transfer coefficient include:
- Fluid properties: The density, viscosity, and thermal conductivity of the fluid can significantly impact the convective heat transfer coefficient.
- Surface roughness: A rough surface can increase the turbulence of the fluid, leading to increased heat transfer and a higher convective heat transfer coefficient.
- Fluid velocity: Increasing the velocity of the fluid can enhance heat transfer by increasing the convection currents and the convective heat transfer coefficient.
Applications of Convective Heat Transfer
Convective heat transfer has numerous practical applications in various fields, including aerospace engineering, chemical engineering, and mechanical engineering. Some examples of applications include:
- Cooling systems: Convective heat transfer is used in cooling systems, such as air conditioning and refrigeration, to transfer heat from a system to the surrounding environment.
- Heat exchangers: Convective heat transfer is used in heat exchangers, such as boilers and condensers, to transfer heat between two fluids.
- Electronic devices: Convective heat transfer is used to cool electronic devices, such as computers and smartphones, by transferring heat to the surrounding air.
Measurement of Convective Heat Transfer Coefficient
The convective heat transfer coefficient can be measured using various experimental techniques, such as hot wire anemometry and laser Doppler velocimetry. These techniques involve measuring the temperature and velocity of the fluid near the surface, as well as the heat transfer rate. The convective heat transfer coefficient can also be calculated using numerical methods, such as computational fluid dynamics (CFD). Some key considerations when measuring the convective heat transfer coefficient include:
- Accuracy: The measurement technique should be accurate and reliable to ensure that the convective heat transfer coefficient is calculated correctly.
- Resolution: The measurement technique should have sufficient resolution to capture the small-scale fluctuations in the fluid velocity and temperature.
- Repeatability: The measurement technique should be repeatable to ensure that the convective heat transfer coefficient is consistent and reliable.
Limitations and Challenges of Convective Heat Transfer
Convective heat transfer has several limitations and challenges, including the complexity of the fluid dynamics and the difficulty of predicting the convective heat transfer coefficient. Some key limitations and challenges include:
- Turbulence: Turbulent flows can be difficult to predict and model, which can make it challenging to calculate the convective heat transfer coefficient.
- Scaling: Scaling the convective heat transfer coefficient from small-scale experiments to large-scale applications can be challenging due to the complexity of the fluid dynamics.
- Non-uniformity: Non-uniformities in the surface temperature and fluid velocity can affect the convective heat transfer coefficient and make it difficult to predict.
How do you calculate the heat transmission by convection?

To calculate the heat transmission by convection, we need to consider the factors that affect the convective heat transfer coefficient, such as the fluid properties, velocity, and temperature difference. The convective heat transfer coefficient is a measure of the rate at which heat is transferred between a solid surface and a fluid in motion. The calculation involves the use of empirical correlations and dimensionless numbers, such as the Nusselt number, Reynolds number, and Prandtl number.
Introduction to Convective Heat Transfer
Convective heat transfer is a complex process that involves the transfer of heat between a solid surface and a fluid in motion. The convective heat transfer coefficient is a critical parameter in designing and optimizing systems that involve heat transfer, such as heat exchangers and electronic cooling systems. To calculate the convective heat transfer coefficient, we need to consider the following factors:
- Fluid properties, such as density, viscosity, and specific heat capacity
- Velocity of the fluid, which affects the turbulence and laminar flow
- Temperature difference between the solid surface and the fluid
Empirical Correlations for Convective Heat Transfer
Empirical correlations are used to predict the convective heat transfer coefficient for different flow regimes and geometries. These correlations are based on experimental data and are often expressed in terms of dimensionless numbers, such as the Nusselt number, Reynolds number, and Prandtl number. For example, the Dittus-Boelter equation is a commonly used correlation for turbulent flow in circular tubes:
- The equation is based on the Nusselt number, Reynolds number, and Prandtl number
- The correlation is valid for turbulent flow with a Reynolds number greater than 10,000
- The equation is used to predict the convective heat transfer coefficient for circular tubes
Dimensionless Numbers in Convective Heat Transfer
Dimensionless numbers play a crucial role in convective heat transfer as they allow us to scale the problem and predict the heat transfer coefficient. The Nusselt number, Reynolds number, and Prandtl number are the most commonly used dimensionless numbers in convective heat transfer. These numbers are defined as:
- The Nusselt number is the ratio of convective heat transfer to conductive heat transfer
- The Reynolds number is the ratio of inertial forces to viscous forces
- The Prandtl number is the ratio of momentum diffusivity to thermal diffusivity
Fluid Properties and Convective Heat Transfer
Fluid properties, such as density, viscosity, and specific heat capacity, play a significant role in convective heat transfer. The density and viscosity of the fluid affect the Reynolds number, while the specific heat capacity affects the Prandtl number. The fluid properties also affect the convective heat transfer coefficient, which is a measure of the rate at which heat is transferred between the solid surface and the fluid:
- The density of the fluid affects the inertial forces and viscous forces
- The viscosity of the fluid affects the laminar flow and turbulent flow
- The specific heat capacity of the fluid affects the thermal energy transfer
Applications of Convective Heat Transfer
Convective heat transfer has numerous applications in engineering and industry, including heat exchangers, electronic cooling systems, and aerospace engineering. The convective heat transfer coefficient is a critical parameter in designing and optimizing these systems. The empirical correlations and dimensionless numbers are used to predict the heat transfer coefficient and optimize the system:
- Heat exchangers are used to transfer heat between two fluids
- Electronic cooling systems are used to cool electronic devices
- Aerospace engineering involves the design of heat shields and thermal protection systems
What is the formula for calculating heat transfer?

The formula for calculating heat transfer is a complex one, involving several factors such as the temperature difference, thermal conductivity, and surface area of the objects involved. The most common formula used to calculate heat transfer is Q = (U A) ΔT, where Q is the amount of heat transferred, U is the overall heat transfer coefficient, A is the surface area of the object, and ΔT is the temperature difference between the two objects.
Introduction to Heat Transfer Formulas
The formula for calculating heat transfer is based on the principles of thermodynamics and is used to determine the amount of heat that is transferred from one object to another. The formula takes into account the thermal properties of the objects involved, such as their thermal conductivity and specific heat capacity. Some of the key factors that affect heat transfer include:
- Temperature difference: The greater the temperature difference between the two objects, the more heat is transferred.
- Thermal conductivity: The ability of a material to conduct heat is measured by its thermal conductivity, with higher values indicating better heat transfer.
- Surface area: The larger the surface area of the objects involved, the more heat is transferred.
Conductive Heat Transfer
Conductive heat transfer occurs when there is a direct contact between two objects, allowing heat to be transferred through the collisions of particles. The formula for conductive heat transfer is Q = (k A) ΔT / L, where k is the thermal conductivity of the material, A is the surface area, ΔT is the temperature difference, and L is the length of the material. Some of the key factors that affect conductive heat transfer include:
- Thermal conductivity: The ability of a material to conduct heat is measured by its thermal conductivity, with higher values indicating better heat transfer.
- Temperature difference: The greater the temperature difference between the two objects, the more heat is transferred.
- Surface area: The larger the surface area of the objects involved, the more heat is transferred.
Convective Heat Transfer
Convective heat transfer occurs when there is a fluid involved, such as air or water, which helps to transfer heat through the movement of particles. The formula for convective heat transfer is Q = (h A) ΔT, where h is the convective heat transfer coefficient, A is the surface area, and ΔT is the temperature difference. Some of the key factors that affect convective heat transfer include:
- Convective heat transfer coefficient: The ability of a fluid to transfer heat is measured by its convective heat transfer coefficient, with higher values indicating better heat transfer.
- Temperature difference: The greater the temperature difference between the two objects, the more heat is transferred.
- Surface area: The larger the surface area of the objects involved, the more heat is transferred.
Radiative Heat Transfer
Radiative heat transfer occurs when there is a temperature difference between two objects, causing them to emit and absorb radiation. The formula for radiative heat transfer is Q = ε σ A (T1^4 - T2^4), where ε is the emissivity of the objects, σ is the Stefan-Boltzmann constant, A is the surface area, and T1 and T2 are the temperatures of the two objects. Some of the key factors that affect radiative heat transfer include:
- Emissivity: The ability of an object to emit and absorb radiation is measured by its emissivity, with higher values indicating better heat transfer.
- Temperature difference: The greater the temperature difference between the two objects, the more heat is transferred.
- Surface area: The larger the surface area of the objects involved, the more heat is transferred.
Applications of Heat Transfer Formulas
The formulas for calculating heat transfer have numerous practical applications in various fields, including engineering, physics, and chemistry. Some of the key applications include:
- Designing heating and cooling systems: Heat transfer formulas are used to determine the amount of heat that needs to be transferred in order to achieve a desired temperature.
- Developing thermal insulation materials: Heat transfer formulas are used to determine the thermal properties of materials, which is essential for developing effective thermal insulation materials.
- Understanding climate change: Heat transfer formulas are used to understand the global energy balance, which is essential for understanding climate change.
Frequently Asked Questions (FAQs)
What is Convective Heat Transfer and its Importance in Engineering?
Convective heat transfer is a fundamental concept in engineering that involves the transfer of heat between a solid surface and a fluid (liquid or gas) in motion. This process is crucial in various engineering applications, including heat exchangers, electronic cooling systems, and thermal management. The convection equation, which describes the rate of heat transfer due to convection, is a key tool for engineers to analyze and design systems that involve convective heat transfer. The equation takes into account factors such as the temperature difference between the solid surface and the fluid, the fluid velocity, and the thermal properties of the fluid. By understanding and applying the principles of convective heat transfer, engineers can optimize the performance of systems, reduce energy consumption, and improve overall efficiency.
How Does the Convection Equation Work and What are its Limitations?
The convection equation is a mathematical model that describes the rate of heat transfer due to convection. It is based on the principles of fluid dynamics and heat transfer, and it takes into account factors such as the boundary layer, turbulence, and heat transfer coefficients. The equation is typically expressed in terms of the Nusselt number, which is a dimensionless quantity that characterizes the convective heat transfer process. While the convection equation is a powerful tool for analyzing convective heat transfer, it has limitations. For example, it assumes a simplified geometry and constant fluid properties, which may not always be the case in real-world applications. Additionally, the equation can be complex and nonlinear, making it challenging to solve analytically. To overcome these limitations, engineers often use numerical methods or approximations to solve the convection equation and predict the behavior of convective heat transfer systems.
What is the Role of the Calculator in Convective Heat Transfer Analysis?
The calculator is a valuable tool for engineers working with convective heat transfer systems. It allows them to quickly and easily calculate heat transfer rates, temperature distributions, and other important parameters. The calculator can be used to validate designs, optimize performance, and troubleshoot problems in convective heat transfer systems. By inputting the relevant parameters and properties, engineers can use the calculator to generate accurate and reliable results, which can be used to inform design decisions and improve overall system performance. The calculator can also be used to explore the effects of different variables on the convective heat transfer process, such as the impact of fluid velocity or surface roughness on heat transfer rates.
How Can Engineers Apply the Principles of Convective Heat Transfer to Real-World Problems?
Engineers can apply the principles of convective heat transfer to a wide range of real-world problems, including the design of heat exchangers, electronic cooling systems, and thermal management systems. By understanding the fundamentals of convective heat transfer, engineers can optimize system performance, reduce energy consumption, and improve overall efficiency. For example, in the design of heat exchangers, engineers can use the convection equation to predict heat transfer rates and optimize the design of the heat exchanger. In electronic cooling systems, engineers can use the principles of convective heat transfer to design more efficient cooling systems and reduce the risk of overheating. By applying the principles of convective heat transfer, engineers can create innovative solutions to complex problems and improve the performance of a wide range of systems and applications.
Deja una respuesta

Entradas Relacionadas