Bolt Head Friction Torque Formula and Calculator per. MIL-HDBH-60
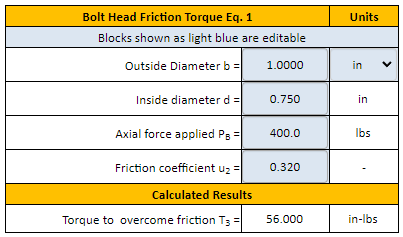
The Bolt Head Friction Torque Formula is a standard calculation method outlined in the MIL-HDBK-60 military handbook. This formula is used to determine the torque required to tighten or loosen a bolt, taking into account the frictional forces present between the bolt head and the surrounding material. By using the formula, engineers and technicians can ensure that bolts are properly secured, reducing the risk of equipment failure or damage. The calculator provided per MIL-HDBK-60 guidelines enables accurate and efficient calculation of the required torque. This formula is crucial in various industries, including aerospace and defense.
- Bolt Head Friction Torque Formula and Calculator per. MIL-HDBK-60
- What is the formula for torque due to friction?
- What is the formula for bolt tightening torque?
- How do you calculate the friction of a bolt?
- What is the coefficient of friction for the nut face or bolt head?
-
Frequently Asked Questions (FAQs)
- What is the Bolt Head Friction Torque Formula and Calculator according to MIL-HDBK-60?
- How does the Bolt Head Friction Torque Formula and Calculator account for variability in friction coefficients?
- Can the Bolt Head Friction Torque Formula and Calculator be used for non-military applications?
- How is the Bolt Head Friction Torque Formula and Calculator used in conjunction with other engineering tools and software?
Bolt Head Friction Torque Formula and Calculator per. MIL-HDBK-60
The Bolt Head Friction Torque Formula and Calculator per. MIL-HDBK-60 is a widely used method for calculating the torque required to tighten or loosen a bolt. This formula takes into account the coefficient of friction between the bolt head and the surface it is in contact with, as well as the bolt diameter and thread pitch. The formula is as follows: T = (K D P) / 12, where T is the torque, K is the coefficient of friction, D is the bolt diameter, and P is the thread pitch.
Introduction to Bolt Head Friction Torque Formula
The Bolt Head Friction Torque Formula is a simple and effective way to calculate the torque required to tighten or loosen a bolt. This formula is based on the principle of friction, which states that the force required to move an object is proportional to the normal force and the coefficient of friction. In the case of a bolt, the normal force is the force exerted by the bolt head on the surface it is in contact with, and the coefficient of friction is a measure of the frictional resistance between the two surfaces.
Understanding the Coefficient of Friction
The coefficient of friction is a critical component of the Bolt Head Friction Torque Formula. This value represents the frictional resistance between the bolt head and the surface it is in contact with. The coefficient of friction can vary depending on the materials involved and the surface roughness. For example, a smooth surface will have a lower coefficient of friction than a rough surface. The following table lists some common coefficients of friction for different materials:
| Material | Coefficient of Friction |
|---|---|
| Steel on Steel | 0.1-0.2 |
| Aluminum on Aluminum | 0.2-0.3 |
| Brass on Steel | 0.1-0.2 |
Calculating Torque using the Formula
To calculate the torque required to tighten or loosen a bolt using the Bolt Head Friction Torque Formula, you need to know the bolt diameter, thread pitch, and coefficient of friction. The formula is as follows: T = (K D P) / 12. For example, if you have a bolt with a diameter of 1 inch, a thread pitch of 1/4 inch, and a coefficient of friction of 0.15, the torque required to tighten the bolt would be: T = (0.15 1 0.25) / 12 = 0.0031 foot-pounds.
Using a Calculator to Simplify the Process
To simplify the process of calculating torque using the Bolt Head Friction Torque Formula, you can use a calculator. There are many online calculators available that can perform the calculation for you, or you can create your own spreadsheet to do the calculation. The calculator will take into account the bolt diameter, thread pitch, and coefficient of friction, and will output the torque required to tighten or loosen the bolt.
Common Applications of the Bolt Head Friction Torque Formula
The Bolt Head Friction Torque Formula has many practical applications in the field of engineering and manufacturing. For example, it is commonly used in the aerospace industry to ensure that bolts are tightened to the correct torque to prevent loosening or over-tightening. It is also used in the automotive industry to specify the torque required to tighten bolts on engines and transmissions. Additionally, it is used in the construction industry to ensure that bolts are tightened to the correct torque to prevent structural failure. The following table lists some common applications of the formula:
| Industry | Application |
|---|---|
| Aerospace | Aircraft and Spacecraft assembly |
| Automotive | Engine and Transmission assembly |
| Construction | Building and Bridge construction |
What is the formula for torque due to friction?

The formula for torque due to friction is τ = r x F, where τ is the torque, r is the radius of the object, and F is the frictional force. This formula is used to calculate the torque caused by friction, which is a rotational force that can cause an object to rotate or change its rotational motion.
Understanding the Concept of Torque Due to Friction
The concept of torque due to friction is crucial in understanding how frictional forces affect the rotational motion of an object. The formula τ = r x F shows that the torque due to friction is dependent on the radius of the object and the frictional force acting on it. To calculate the torque due to friction, we need to know the radius of the object and the frictional force acting on it.
- The frictional force is the force that opposes the motion of an object, and it is dependent on the coefficient of friction and the normal force acting on the object.
- The radius of the object is the distance from the axis of rotation to the point where the frictional force is acting.
- The torque due to friction is a vector quantity, which means it has both magnitude and direction.
Factors Affecting Torque Due to Friction
Several factors can affect the torque due to friction, including the coefficient of friction, the normal force, and the radius of the object. The coefficient of friction is a measure of the frictional force between two surfaces, and it can vary depending on the surface roughness and the materials involved.
- The coefficient of friction is an important factor in determining the torque due to friction, as it affects the magnitude of the frictional force.
- The normal force is another factor that can affect the torque due to friction, as it determines the magnitude of the frictional force.
- The radius of the object is also an important factor, as it determines the lever arm of the frictional force.
Applications of Torque Due to Friction
The concept of torque due to friction has many practical applications, including the design of machinery and mechanisms. In engineering, the torque due to friction is an important consideration in the design of surfaces and bearings, as it can affect the efficiency and reliability of a system.
- The torque due to friction is an important consideration in the design of transmissions and gears.
- The coefficient of friction is an important factor in determining the torque due to friction, and it can be optimized through the use of lubricants and surface coatings.
- The radius of the object is also an important factor, as it determines the lever arm of the frictional force.
Calculating Torque Due to Friction
To calculate the torque due to friction, we need to know the radius of the object and the frictional force acting on it. The formula τ = r x F can be used to calculate the torque, where τ is the torque, r is the radius, and F is the frictional force.
- The frictional force can be calculated using the formula F = μ x N, where μ is the coefficient of friction and N is the normal force.
- The radius of the object can be measured directly, or it can be calculated using the dimensions of the object.
- The torque due to friction can be calculated by multiplying the radius and the frictional force, and taking into account the direction of the forces.
Real-World Examples of Torque Due to Friction
The concept of torque due to friction is ubiquitous in real-world applications, from the brakes on a car to the gears in a transmission. In each of these examples, the torque due to friction plays a critical role in determining the performance and efficiency of the system.
- The torque due to friction is an important consideration in the design of brake systems, as it affects the stopping distance and the heat generated by the brakes.
- The coefficient of friction is an important factor in determining the torque due to friction, and it can be optimized through the use of lubricants and surface coatings.
- The radius of the object is also an important factor, as it determines the lever arm of the frictional force.
What is the formula for bolt tightening torque?

The formula for bolt tightening torque is a calculation that determines the amount of torque required to tighten a bolt to a specific level of tension. The formula is: T = (K x D x P) / 12, where T is the torque, K is the nut factor, D is the diameter of the bolt, and P is the preload. This formula is used to ensure that the bolt is tightened to a safe and effective level, without being over-tightened or under-tightened.
Understanding the Nut Factor
The nut factor is a critical component of the bolt tightening torque formula. It is a value that represents the frictional characteristics of the bolt and nut, and is typically determined through experimentation or consulting a torque chart. The nut factor can vary depending on the type of bolt and nut being used, as well as the lubrication and surface conditions.
- The nut factor can range from 0.10 to 0.30, depending on the specific application.
- A higher nut factor indicates a higher level of friction, which requires more torque to achieve the same level of preload.
- Consulting a torque chart or consulting with a mechanical engineer can help determine the correct nut factor for a specific application.
Calculating Preload
The preload is the amount of tension that is applied to the bolt when it is tightened. It is an important factor in determining the bolt tightening torque, as it affects the stress and strain on the bolt and surrounding materials. The preload can be calculated using the formula: P = (A x S) / 2, where P is the preload, A is the cross-sectional area of the bolt, and S is the yield strength of the material.
- The preload should be calculated based on the specific requirements of the application, taking into account factors such as safety and performance.
- A higher preload can provide greater security and stability, but can also increase the risk of over-tightening.
- Consulting with a mechanical engineer or referencing a design manual can help determine the correct preload for a specific application.
Factors Affecting Bolt Tightening Torque
There are several factors that can affect the bolt tightening torque, including the bolt material, nut material, surface roughness, and lubrication. These factors can impact the friction and stress on the bolt and surrounding materials, and must be taken into account when calculating the bolt tightening torque.
- The bolt material and nut material can affect the coefficient of friction, which impacts the torque required to achieve a specific level of preload.
- The surface roughness of the bolt and nut can also affect the friction, with rougher surfaces requiring more torque to achieve the same level of preload.
- Lubrication can reduce the friction and wear on the bolt and nut, but can also affect the preload and torque required.
Importance of Accurate Torque Calculation
Accurate calculation of the bolt tightening torque is critical to ensure the safety and performance of the application. Over-tightening can lead to damage or failure of the bolt or surrounding materials, while under-tightening can result in loosening or vibration.
- Over-tightening can cause excessive stress and strain on the bolt and surrounding materials, leading to failure or damage.
- Under-tightening can result in loosening or vibration, which can affect the performance and safety of the application.
- Consulting with a mechanical engineer or referencing a design manual can help ensure accurate calculation of the bolt tightening torque.
Applications of Bolt Tightening Torque Formula
The bolt tightening torque formula has a wide range of applications, including automotive, aerospace, construction, and manufacturing. It is used to ensure the safety and performance of bolts and fasteners in various industries, and is an essential tool for engineers and technicians.
- The automotive industry uses the bolt tightening torque formula to ensure the safety and performance of vehicles and engines.
- The aerospace industry uses the formula to ensure the safety and performance of aircraft and spacecraft.
- The construction industry uses the formula to ensure the safety and performance of buildings and structures.
How do you calculate the friction of a bolt?
To calculate the friction of a bolt, you need to consider the coefficient of friction between the bolt and the surrounding material, as well as the normal force acting on the bolt. The frictional force can be calculated using the formula F = μN, where F is the frictional force, μ is the coefficient of friction, and N is the normal force. This formula is commonly used in engineering and physics to determine the frictional force acting on an object.
Understanding the Coefficient of Friction
The coefficient of friction is a measure of the resistance to motion between two surfaces. It is a dimensionless quantity that depends on the material properties of the surfaces in contact. To calculate the coefficient of friction, you need to consider the surface roughness, temperature, and humidity of the environment. The coefficient of friction can be determined experimentally using a friction test.
- Static friction: the frictional force that prevents an object from moving.
- Kinetic friction: the frictional force that opposes the motion of an object.
- Coefficient of friction: a dimensionless quantity that depends on the material properties of the surfaces in contact.
Calculating the Normal Force
The normal force is the perpendicular force acting on an object. To calculate the normal force, you need to consider the weight of the object and the angle of the surface. The normal force can be calculated using the formula N = mgcos(θ), where N is the normal force, m is the mass of the object, g is the acceleration due to gravity, and θ is the angle of the surface.
- Weight: the force acting on an object due to gravity.
- Angle: the inclination of the surface relative to the horizontal.
- Normal force: the perpendicular force acting on an object.
Determining the Frictional Force
The frictional force can be calculated using the formula F = μN, where F is the frictional force, μ is the coefficient of friction, and N is the normal force. This formula is commonly used in engineering and physics to determine the frictional force acting on an object. The frictional force depends on the coefficient of friction and the normal force.
- Frictional force: the force that opposes the motion of an object.
- Coefficient of friction: a dimensionless quantity that depends on the material properties of the surfaces in contact.
- Normal force: the perpendicular force acting on an object.
Considering the Bolt Material
The bolt material plays a crucial role in determining the frictional force. Different materials have different coefficients of friction, which affect the frictional force. For example, stainless steel has a higher coefficient of friction than brass. The bolt material should be chosen based on the requirements of the application.
- Stainless steel: a corrosion-resistant material with a high coefficient of friction.
- Brass: a ductile material with a low coefficient of friction.
- Aluminum: a lightweight material with a low coefficient of friction.
Applying the Calculations to Real-World Scenarios
The calculations for frictional force can be applied to real-world scenarios such as engine design, mechanical systems, and structural engineering. The frictional force must be considered when designing machines and structures to ensure safe and efficient operation. The coefficient of friction and normal force must be carefully calculated to determine the frictional force.
- Engine design: the frictional force must be considered when designing engines to ensure efficient operation.
- Mechanical systems: the frictional force must be considered when designing mechanical systems to ensure safe operation.
- Structural engineering: the frictional force must be considered when designing structures to ensure stable operation.
What is the coefficient of friction for the nut face or bolt head?

The coefficient of friction for the nut face or bolt head is a critical factor in determining the torque required to tighten or loosen a fastener. This coefficient is a measure of the frictional force that opposes the motion between two surfaces in contact, such as the nut face and the bolt head. The coefficient of friction can vary depending on the surface roughness, material properties, and lubrication conditions.
Types of Coefficient of Friction
The coefficient of friction for the nut face or bolt head can be categorized into two main types: static friction and kinetic friction. Static friction occurs when the nut or bolt is at rest, while kinetic friction occurs when it is in motion. The coefficient of static friction is typically higher than the coefficient of kinetic friction. Some of the key factors that affect the coefficient of friction include:
- Surface roughness: A rougher surface can increase the coefficient of friction
- Material properties: Different materials can have varying coefficients of friction
- Lubrication conditions: The presence of lubricants can reduce the coefficient of friction
Factors Affecting Coefficient of Friction
Several factors can influence the coefficient of friction for the nut face or bolt head, including temperature, humidity, and contamination. For example, high temperatures can reduce the coefficient of friction, while humidity and contamination can increase it. Additionally, the surface finish and geometry of the nut face and bolt head can also impact the coefficient of friction. Some of the key factors to consider include:
- Temperature: High temperatures can reduce the coefficient of friction
- Humidity: High humidity can increase the coefficient of friction
- Contamination: Presence of contaminants can increase the coefficient of friction
Measurement of Coefficient of Friction
The coefficient of friction for the nut face or bolt head can be measured using various experimental techniques, such as the inclined plane method or the rotating drum method. These methods involve measuring the force required to move the nut or bolt along a surface or around a rotating drum. The coefficient of friction is then calculated based on the measured force and the normal force. Some of the key considerations for measuring the coefficient of friction include:
- Experimental technique: Choice of experimental technique can impact the accuracy of the measurement
- Surface preparation: Proper surface preparation is essential for accurate measurement
- Force measurement: Accurate force measurement is critical for calculating the coefficient of friction
Applications of Coefficient of Friction
The coefficient of friction for the nut face or bolt head has practical applications in various fields, such as engineering, manufacturing, and construction. For example, understanding the coefficient of friction is essential for designing safe and efficient fastening systems. Additionally, the coefficient of friction can impact the performance and reliability of mechanical systems. Some of the key applications of the coefficient of friction include:
- Fastening systems: Understanding the coefficient of friction is essential for designing safe and efficient fastening systems
- Mechanical systems: The coefficient of friction can impact the performance and reliability of mechanical systems
- Construction: The coefficient of friction is important for ensuring the safety and stability of structures
Importance of Coefficient of Friction
The coefficient of friction for the nut face or bolt head is a critical parameter in ensuring the safety and reliability of mechanical systems. A low coefficient of friction can lead to loosening of the fastener, while a high coefficient of friction can result in over-tightening. Therefore, understanding and controlling the coefficient of friction is essential for preventing failures and ensuring the integrity of mechanical systems. Some of the key considerations for ensuring the importance of the coefficient of friction include:
- Safety: A low coefficient of friction can lead to loosening of the fastener, compromising safety
- Reliability: A high coefficient of friction can result in over-tightening, compromising reliability
- Failure prevention: Understanding and controlling the coefficient of friction is essential for preventing failures
Frequently Asked Questions (FAQs)
What is the Bolt Head Friction Torque Formula and Calculator according to MIL-HDBK-60?
The Bolt Head Friction Torque Formula and Calculator per MIL-HDBK-60 is a standardized method for calculating the friction torque required to tighten or loosen a bolt. This formula takes into account various factors such as the bolt diameter, thread pitch, coefficient of friction, and applied torque. The MIL-HDBK-60 is a military standard that provides guidelines for the design and testing of fasteners, including bolts and screws. The formula and calculator provided in this standard are used to ensure that the fasteners are properly tightened or loosened to prevent over-tightening or under-tightening, which can lead to failure or damage to the fastener or the surrounding material. The calculator is typically used in engineering and manufacturing applications where precision and accuracy are crucial.
How does the Bolt Head Friction Torque Formula and Calculator account for variability in friction coefficients?
The Bolt Head Friction Torque Formula and Calculator per MIL-HDBK-60 accounts for variability in friction coefficients by using a statistical approach to determine the mean and standard deviation of the friction coefficient. This approach takes into account the variability in the coefficient of friction due to factors such as surface roughness, lubrication, and material properties. The formula uses a nominal value for the friction coefficient and then applies a safety factor to account for any uncertainty or variability in the coefficient of friction. This ensures that the calculated friction torque is conservative and takes into account any potential errors or uncertainties in the friction coefficient. Additionally, the calculator provides a range of values for the friction torque based on the uncertainty in the friction coefficient, allowing the user to select the most appropriate value for their specific application.
Can the Bolt Head Friction Torque Formula and Calculator be used for non-military applications?
Yes, the Bolt Head Friction Torque Formula and Calculator per MIL-HDBK-60 can be used for non-military applications. While the standard was originally developed for military applications, the formula and calculator are based on fundamental principles of physics and mechanics that are applicable to a wide range of industries and applications. The formula and calculator can be used in aerospace, automotive, industrial, and commercial applications where fasteners are used to assemble or disassemble components. The accuracy and reliability of the formula and calculator make them a valuable tool for engineers and technicians working in these fields. Additionally, the formula and calculator can be used to validate or verify the results of other calculations or simulations, providing an independent check on the accuracy of the results.
How is the Bolt Head Friction Torque Formula and Calculator used in conjunction with other engineering tools and software?
The Bolt Head Friction Torque Formula and Calculator per MIL-HDBK-60 is often used in conjunction with other engineering tools and software to provide a comprehensive analysis of the fastening system. For example, the formula and calculator can be used in conjunction with finite element analysis (FEA) software to model the stress and strain on the fastener and surrounding material. The formula and calculator can also be used with computer-aided design (CAD) software to design and optimize the fastening system. Additionally, the formula and calculator can be used with testing and validation software to verify the results of experiments or simulations. The output from the formula and calculator can be imported into other software or spreadsheets for further analysis or processing, making it a versatile and powerful tool for engineers and technicians. The integration of the formula and calculator with other engineering tools and software provides a seamless and efficient workflow for designing, analyzing, and optimizing fastening systems.
Deja una respuesta

Entradas Relacionadas