Beam Three Support Two Loads Reactions Equations and Calculator
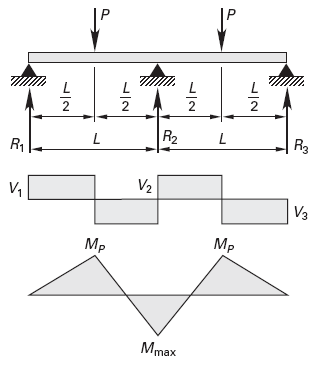
The beam three support two loads is a structural system commonly used in building design. It consists of a horizontal beam supported by three vertical columns, with two external loads applied to the beam. To analyze this system, engineers use reactions equations to determine the forces acting on each support. A calculator can be used to simplify the process, providing a quick and accurate solution. The reactions equations and calculator for beam three support two loads will be discussed in detail, including the assumptions, equations, and applications of this structural system. Various examples will illustrate its practical use.
- Beam Three Support Two Loads Reactions Equations and Calculator
- How to calculate support reactions in beams?
- What is a beam calculator?
- How do you calculate beams?
- How do you calculate simply supported beams?
-
Frequently Asked Questions (FAQs)
- What is the concept of beam three support two loads reactions equations and calculator?
- How do the beam three support two loads reactions equations and calculator work?
- What are the assumptions made in the beam three support two loads reactions equations and calculator?
- What are the limitations of the beam three support two loads reactions equations and calculator?
Beam Three Support Two Loads Reactions Equations and Calculator
The Beam Three Support Two Loads Reactions Equations and Calculator is a mathematical model used to determine the reactions at the supports of a beam that is subject to two loads. This model is commonly used in structural analysis and engineering to ensure that the beam can withstand the applied loads without failure. The model takes into account the weight and distribution of the loads, as well as the properties of the beam itself, such as its length, width, and material.
Introduction to Beam Reactions
Beam reactions refer to the forces that are exerted on a beam by its supports. These forces can be either upward or downward, depending on the type of support and the load that is applied. The Beam Three Support Two Loads Reactions Equations and Calculator is used to determine the magnitude and direction of these forces. The calculator uses equations that are based on the principles of statics and mechanics to calculate the reactions at the supports.
Types of Beam Supports
There are several types of beam supports that can be used, including simply supported, fixed, and roller supports. Each type of support has its own unique characteristics and properties, and the Beam Three Support Two Loads Reactions Equations and Calculator can be used to determine the reactions at each type of support. The calculator can also be used to determine the moments and shear forces at each support.
Beam Reactions Equations
The Beam Three Support Two Loads Reactions Equions are based on the following equations:
| Equation | Description |
|---|---|
| ΣF = 0 | The sum of the forces acting on the beam is equal to zero. |
| ΣM = 0 | The sum of the moments acting on the beam is equal to zero. |
These equations are used to calculate the reactions at the supports and to determine the moments and shear forces at each support.
Beam Reactions Calculator
The Beam Three Support Two Loads Reactions Calculator is a software program that is used to calculate the reactions at the supports of a beam that is subject to two loads. The calculator uses the equations that are described above to determine the reactions and to calculate the moments and shear forces at each support. The calculator can be used to determine the reactions for a variety of beam configurations, including simply supported, fixed, and roller supports.
Applications of Beam Reactions
The Beam Three Support Two Loads Reactions Equations and Calculator have a number of practical applications in engineering and structural analysis. The calculator can be used to design beams that are subject to multiple loads, such as buildings, bridges, and highways. The calculator can also be used to determine the reactions at the supports of a beam that is subject to dynamic loads, such as earthquakes or wind. Overall, the Beam Three Support Two Loads Reactions Equations and Calculator are an important tool for engineers and structural analysts who need to design and analyze beams that are subject to multiple loads.
How to calculate support reactions in beams?

To calculate support reactions in beams, it is essential to understand the concept of equilibrium and the forces acting on the beam. The support reactions are the forces exerted by the supports on the beam, and they can be calculated using the equilibrium equations. The equilibrium equations are based on the principle that the sum of all forces and moments acting on a rigid body must be equal to zero.
Understanding the Types of Supports
To calculate the support reactions, it is crucial to understand the types of supports that are used to restrain the beam. The most common types of supports are roller supports, pin supports, and fixed supports. Each type of support provides a different type of restraint to the beam, and this affects the support reactions. The support reactions can be calculated using the following steps:
- Draw a free-body diagram of the beam, showing all the forces and moments acting on it.
- Identify the unknown support reactions and the known forces and moments.
- Apply the equilibrium equations to the beam, using the principle of equilibrium.
Calculating Support Reactions using Equilibrium Equations
The equilibrium equations are used to calculate the support reactions in a beam. The equilibrium equations are based on the principle of equilibrium, which states that the sum of all forces and moments acting on a rigid body must be equal to zero. The equilibrium equations can be applied to the beam as follows:
- Determine the sum of all forces acting on the beam in the x-direction and the y-direction.
- Determine the sum of all moments acting on the beam about a point.
- Use the equilibrium equations to calculate the unknown support reactions.
Using the Principle of Superposition
The principle of superposition can be used to calculate the support reactions in a beam. The principle of superposition states that the effect of multiple loads on a beam is equal to the sum of the effects of each load acting separately. The principle of superposition can be applied to the beam as follows:
- Calculate the support reactions for each load acting separately on the beam.
- Use the principle of superposition to calculate the total support reactions due to all the loads.
- Verify that the total support reactions are in equilibrium with the external loads.
Considering the Effects of Distributed Loads
Distributed loads can have a significant effect on the support reactions in a beam. A distributed load is a load that is spread out over a length of the beam, rather than being concentrated at a point. The effects of distributed loads can be calculated using the following steps:
- Calculate the total load due to the distributed load.
- Determine the location of the center of gravity of the distributed load.
- Use the equilibrium equations to calculate the support reactions due to the distributed load.
Applying the Method of Virtual Work
The method of virtual work can be used to calculate the support reactions in a beam. The method of virtual work is based on the principle of conservation of energy, which states that the work done by the external forces on a system is equal to the change in energy of the system. The method of virtual work can be applied to the beam as follows:
- Calculate the virtual work done by the external forces on the beam.
- Determine the change in energy of the beam due to the virtual displacement.
- Use the method of virtual work to calculate the support reactions.
What is a beam calculator?

A beam calculator is a tool used to calculate the stress, strain, and deflection of a beam under various loads and conditions. It is a vital tool for engineers, architects, and builders to ensure the structural integrity of a building or a structure. The calculator takes into account the material properties, beam dimensions, and load conditions to provide accurate calculations.
What is the purpose of a beam calculator?
The primary purpose of a beam calculator is to determine the load-carrying capacity of a beam and to ensure that it can withstand the applied loads without failing. This is achieved by calculating the bending moment, shear force, and deflection of the beam under various load conditions. The calculator also helps to identify the critical points of the beam where the stress and strain are maximum.
- The beam calculator calculates the maximum stress and strain in the beam.
- The calculator determines the deflection of the beam under load.
- The beam calculator helps to identify the critical points of the beam where the stress and strain are maximum.
How does a beam calculator work?
A beam calculator works by using mathematical formulas and algorithms to calculate the stress, strain, and deflection of a beam. The calculator takes into account the material properties, such as the modulus of elasticity and Poisson's ratio, as well as the beam dimensions, such as the length, width, and height. The calculator also considers the load conditions, including the type and magnitude of the loads.
- The beam calculator uses mathematical formulas to calculate the stress and strain in the beam.
- The calculator takes into account the material properties of the beam.
- The beam calculator considers the load conditions, including the type and magnitude of the loads.
What are the benefits of using a beam calculator?
Using a beam calculator provides several benefits, including increased accuracy, reduced errors, and improved safety. The calculator helps to ensure that the beam is designed to withstand the applied loads and to prevent failure. The calculator also saves time and effort by providing quick and accurate calculations.
- The beam calculator provides increased accuracy in calculating the stress and strain in the beam.
- The calculator helps to reduce errors and improve safety.
- The beam calculator saves time and effort by providing quick and accurate calculations.
What are the types of beam calculators?
There are several types of beam calculators, including simple beam calculators, continuous beam calculators, and beam column calculators. Each type of calculator is designed to handle specific load conditions and beam configurations. The simple beam calculator is used for simply supported beams, while the continuous beam calculator is used for continuous beams.
- The simple beam calculator is used for simply supported beams.
- The continuous beam calculator is used for continuous beams.
- The beam column calculator is used for beam columns.
How to choose a beam calculator?
Choosing a beam calculator depends on the specific requirements of the project, including the type and magnitude of the loads, as well as the material properties and beam dimensions. It is essential to select a calculator that is reliable, accurate, and easy to use. The calculator should also be able to handle complex load conditions and beam configurations.
- The beam calculator should be reliable and accurate.
- The calculator should be easy to use and user-friendly.
- The beam calculator should be able to handle complex load conditions and beam configurations.
How do you calculate beams?
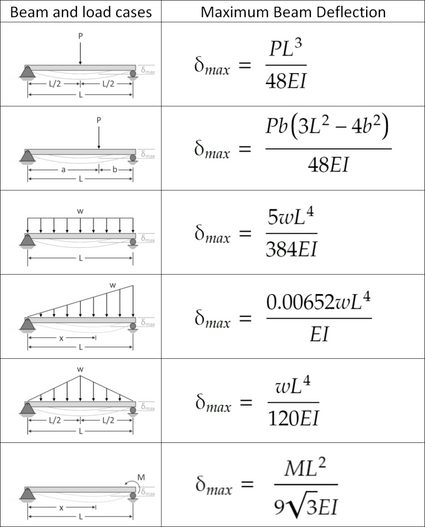
To calculate beams, you need to consider several factors such as the material properties, cross-sectional area, and the loads applied to the beam. The calculation involves determining the stresses and strains that occur in the beam due to the applied loads. This can be done using various methods, including the elastic theory and the plastic theory. The elastic theory assumes that the beam will return to its original shape after the load is removed, while the plastic theory assumes that the beam will deform permanently.
Types of Beams
There are several types of beams, including simply supported beams, cantilever beams, and fixed beams. Each type of beam has its own unique characteristics and boundary conditions that must be considered when calculating the beam's behavior.
- The simply supported beam is supported at both ends and can rotate freely at the supports.
- The cantilever beam is supported at one end and is free at the other end.
- The fixed beam is supported at both ends and is not allowed to rotate at the supports.
Load Calculation
The load calculation is a critical step in calculating beams. The load can be uniformly distributed, concentrated, or varied. The load calculation involves determining the magnitude and direction of the load, as well as the location of the load on the beam.
- The uniformly distributed load is applied evenly along the length of the beam.
- The concentrated load is applied at a single point on the beam.
- The varied load is applied at multiple points on the beam and can vary in magnitude and direction.
Material Properties
The material properties of the beam, such as the modulus of elasticity and the yield strength, play a crucial role in calculating the beam's behavior. The modulus of elasticity determines the stiffness of the beam, while the yield strength determines the maximum stress that the beam can withstand.
- The modulus of elasticity is a measure of the beam's stiffness.
- The yield strength is the maximum stress that the beam can withstand without deforming permanently.
- The poisson's ratio is a measure of the beam's lateral strain.
Boundary Conditions
The boundary conditions of the beam, such as the supports and restraints, must be considered when calculating the beam's behavior. The boundary conditions can affect the deflection and stress of the beam.
- The supports can be simply supported, fixed, or roller supported.
- The restraints can be axial, lateral, or torsional.
- The boundary conditions can affect the natural frequency of the beam.
Beam Deflection
The deflection of the beam is an important aspect of calculating beams. The deflection can be calculated using various methods, including the elastic theory and the plastic theory. The deflection can be affected by the load, material properties, and boundary conditions.
- The elastic theory assumes that the beam will return to its original shape after the load is removed.
- The plastic theory assumes that the beam will deform permanently.
- The deflection can be calculated using the beam equation, which takes into account the load, material properties, and boundary conditions.
How do you calculate simply supported beams?

To calculate simply supported beams, you need to understand the basic principles of beam theory and the formulas that govern the behavior of these structures. A simply supported beam is a type of beam that is supported at both ends by pinned connections, which allow for rotation but not translation. The calculation of simply supported beams involves determining the reactions at the supports, the bending moment and shear force diagrams, and the deflection of the beam.
Understanding the Basic Principles
To calculate simply supported beams, you need to understand the basic principles of statics and solid mechanics. This includes understanding the types of loads that can act on a beam, such as point loads, uniformly distributed loads, and moments. You also need to understand how to calculate the area moment of inertia and the section modulus of the beam's cross-section, which are used to determine the beam's flexural rigidity. The following steps are involved in calculating simply supported beams:
- Determine the reactions at the supports using the equations of equilibrium.
- Calculate the bending moment and shear force diagrams using the loading function.
- Determine the deflection of the beam using the flexure formula.
Calculating Reactions and Bending Moments
Calculating the reactions at the supports and the bending moment diagram is crucial in determining the stress and strain on the beam. The reactions can be calculated using the equations of equilibrium, which involve summing the forces and moments acting on the beam. The bending moment diagram can be calculated using the loading function, which describes the load distribution along the length of the beam. The following steps are involved in calculating the reactions and bending moments:
- Determine the total load acting on the beam.
- Calculate the reactions at the supports using the equations of equilibrium.
- Calculate the bending moment diagram using the loading function.
Calculating Shear Forces and Deflections
Calculating the shear force diagram and the deflection of the beam is also important in determining the stress and strain on the beam. The shear force diagram can be calculated using the loading function, which describes the load distribution along the length of the beam. The deflection of the beam can be calculated using the flexure formula, which involves integrating the curvature of the beam. The following steps are involved in calculating the shear forces and deflections:
- Calculate the shear force diagram using the loading function.
- Determine the deflection of the beam using the flexure formula.
- Calculate the maximum deflection and maximum shear force.
Considering Different Load Cases
Simply supported beams can be subjected to different types of loads, such as point loads, uniformly distributed loads, and moments. Each load case requires a separate calculation to determine the reactions, bending moments, shear forces, and deflections. The following steps are involved in considering different load cases:
- Determine the type of load acting on the beam.
- Calculate the reactions, bending moments, shear forces, and deflections for each load case.
- Combine the results to determine the total stress and strain on the beam.
Using Software and Spreadsheets for Calculations
Calculating simply supported beams can be complex and time-consuming, especially for large structures or complex load cases. To simplify the calculations, software and spreadsheets can be used to automate the process. The following steps are involved in using software and spreadsheets for calculations:
- Choose a suitable software or spreadsheet for calculating simply supported beams.
- Input the beam properties and load data into the software or spreadsheet.
- Run the calculations to determine the reactions, bending moments, shear forces, and deflections.
Frequently Asked Questions (FAQs)
What is the concept of beam three support two loads reactions equations and calculator?
The concept of beam three support two loads reactions equations and calculator is a mathematical model used to calculate the reactions at the supports of a beam that is subjected to two loads. This model is commonly used in civil engineering and structural analysis to determine the forces and moments that act on the beam. The equations used in this model are based on the principles of statics and equilibrium, which state that the sum of all forces and moments acting on the beam must be equal to zero. The calculator! is a tool that is used to simplify the calculation process by solving the equations and providing the reactions at the supports.
How do the beam three support two loads reactions equations and calculator work?
The beam three support two loads reactions equations and calculator work by using the input values of the beam's length, load positions, and load magnitudes to calculate the reactions at the supports. The equations used in this model are based on the principles of statics and equilibrium, which state that the sum of all forces and moments acting on the beam must be equal to zero. The calculator uses these equations to calculate the reactions at the supports, which include the vertical reactions and the moments. The calculator also provides a graphical representation of the beam and the loads, which helps to visualize the problem and understand the results. The results provided by the calculator include the reactions at the supports, the shear force diagram, and the bending moment diagram.
What are the assumptions made in the beam three support two loads reactions equations and calculator?
The beam three support two loads reactions equations and calculator make several assumptions in order to simplify the calculation process. One of the main assumptions is that the beam is a straight beam with a constant cross-sectional area. Another assumption is that the loads are concentrated loads that act at a single point on the beam. The calculator also assumes that the supports are pin supports or roller supports, which provide a reaction force in the vertical direction. Additionally, the calculator assumes that the beam is in a state of static equilibrium, which means that the sum of all forces and moments acting on the beam must be equal to zero. These assumptions are used to simplify the calculation process and provide a reasonable estimate of the reactions at the supports.
What are the limitations of the beam three support two loads reactions equations and calculator?
The beam three support two loads reactions equations and calculator have several limitations that must be considered when using the calculator. One of the main limitations is that the calculator is only applicable to beams with two loads and three supports. The calculator is not applicable to beams with multiple loads or more complex support conditions. Another limitation is that the calculator assumes a linear elastic behavior of the beam, which may not be accurate for beams that are subjected to large deformations or non-linear loads. Additionally, the calculator does not take into account the effects of friction or damping on the beam, which can affect the accuracy of the results. These limitations must be considered when using the calculator and the results must be interpreted with caution and consideration of the assumptions and limitations of the calculator.
Deja una respuesta

Entradas Relacionadas