Triangular Weirs Flow Formula and Calculator
The triangular weir flow formula is a widely used method for calculating the flow rate of water through a triangular notch. This formula is essential in hydraulic engineering, particularly in the design and operation of water measurement structures. The triangular weir flow calculator is a useful tool that applies the formula to determine the flow rate based on the weir's dimensions and water level. By understanding and applying the triangular weir flow formula, engineers can accurately measure water flows in various applications, including irrigation, water supply, and flood control systems. The formula and calculator are valuable resources.
- Understanding the Triangular Weirs Flow Formula and Calculator
- What is the V notch formula?
- How to calculate weir capacity?
- What is the discharge coefficient of a triangular weir?
- What is the formula for weir overflow rate?
-
Frequently Asked Questions (FAQs)
- What is the Triangular Weirs Flow Formula and how is it used in calculations?
- How does the Triangular Weirs Flow Calculator work and what are its limitations?
- What are the advantages and disadvantages of using the Triangular Weirs Flow Formula and Calculator?
- How can the Triangular Weirs Flow Formula and Calculator be applied in real-world scenarios and what are the potential applications?
Understanding the Triangular Weirs Flow Formula and Calculator
The Triangular Weirs Flow Formula is a mathematical equation used to calculate the flow rate of water through a triangular weir, which is a type of weir used to measure the flow rate of water in a channel or stream. The formula is based on the principle that the flow rate of water through a triangular weir is proportional to the head of water above the weir and the angle of the weir. The formula is commonly used in hydraulic engineering and water resources management to measure the flow rate of water in rivers, streams, and canals.
What is a Triangular Weir?
A triangular weir is a type of weir that has a triangular shape, with two sloping sides that meet at a sharp point. The triangular weir is designed to measure the flow rate of water in a channel or stream by creating a hydraulic jump, which is a sudden increase in the water level upstream of the weir. The triangular weir is commonly used in water resources management and hydraulic engineering because it is simple to install and maintain, and it can provide accurate measurements of the flow rate of water.
How Does the Triangular Weirs Flow Formula Work?
The Triangular Weirs Flow Formula works by using the head of water above the weir and the angle of the weir to calculate the flow rate of water through the weir. The formula is based on the principle that the flow rate of water through a triangular weir is proportional to the head of water above the weir and the angle of the weir. The formula is as follows:
Q = (2/3) (g (2 h)^3)^0.5 tan(θ/2)
Where:
Q = flow rate of water through the weir
g = acceleration due to gravity
h = head of water above the weir
θ = angle of the weir
What are the Advantages of Using a Triangular Weir?
The triangular weir has several advantages over other types of weirs, including:
Simple installation and maintenance: The triangular weir is simple to install and maintain, and it can be easily integrated into existing water management systems.
Accurate measurements: The triangular weir can provide accurate measurements of the flow rate of water, which is essential for water resources management and hydraulic engineering.
Low cost: The triangular weir is a relatively low-cost solution for measuring the flow rate of water, compared to other types of weirs.
What are the Limitations of the Triangular Weirs Flow Formula?
The Triangular Weirs Flow Formula has several limitations, including:
Assumes a hydraulic jump: The formula assumes that a hydraulic jump occurs upstream of the weir, which may not always be the case.
Assumes a triangular shape: The formula assumes that the weir has a triangular shape, which may not always be the case.
Limited to subcritical flow: The formula is limited to subcritical flow, and it may not be applicable to supercritical flow.
How to Use the Triangular Weirs Flow Calculator
The Triangular Weirs Flow Calculator is a tool that can be used to calculate the flow rate of water through a triangular weir. The calculator uses the Triangular Weirs Flow Formula to calculate the flow rate of water, and it takes into account the head of water above the weir and the angle of the weir. The calculator is simple to use, and it can provide accurate measurements of the flow rate of water.
| Parameter | Unit | Description |
|---|---|---|
| Head | m | The head of water above the weir |
| Angle | ° | The angle of the weir |
| Flow Rate | m³/s | The flow rate of water through the weir |
What is the V notch formula?
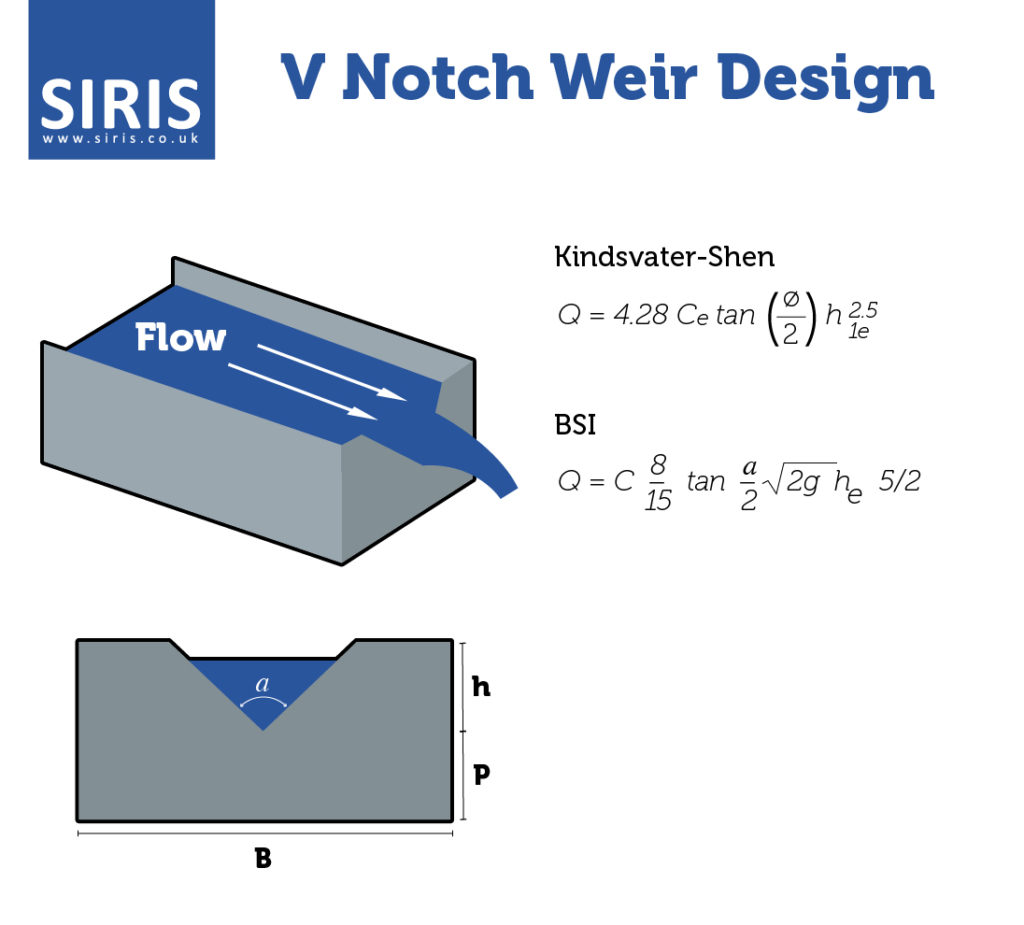
The V notch formula is a mathematical equation used to calculate the flow rate of a fluid through a V-shaped notch. The formula is based on the principle of conservation of mass and energy and is commonly used in hydraulics and fluid mechanics. The V notch formula is given by: Q = (8/15) sqrt(2 g) tan(theta/2) h^2.5, where Q is the flow rate, g is the acceleration due to gravity, theta is the angle of the V notch, and h is the height of the fluid above the bottom of the notch.
Derivation of the V Notch Formula
The derivation of the V notch formula involves the application of the Bernoulli's equation and the equation of continuity. The formula is derived by considering the energy balance and mass balance of the fluid as it flows through the V notch. Some key points to consider when deriving the V notch formula are:
- The flow rate is proportional to the height of the fluid above the bottom of the notch.
- The angle of the V notch affects the velocity of the fluid as it flows through the notch.
- The acceleration due to gravity plays a significant role in determining the flow rate.
Applications of the V Notch Formula
The V notch formula has a wide range of applications in hydraulics and fluid mechanics. Some of the key applications include:
- Flow measurement: The V notch formula can be used to measure the flow rate of a fluid in a channel or pipe.
- Irrigation systems: The V notch formula can be used to design and optimize irrigation systems for agricultural and landscape applications.
- Water supply systems: The V notch formula can be used to design and optimize water supply systems for municipal and industrial applications.
Limitations of the V Notch Formula
The V notch formula has several limitations that must be considered when applying it to real-world problems. Some of the key limitations include:
- Assumes a steady state flow condition, which may not always be the case in practice.
- Assumes a frictionless flow, which can lead to errors if the fluid is viscous or if there are rough surfaces involved.
- Does not account for turbulence or complex flow patterns that may occur in certain situations.
Comparison with Other Flow Measurement Methods
The V notch formula can be compared to other flow measurement methods, such as the orifice plate and the venturi tube. Some key points to consider when comparing these methods are:
- Accuracy: The V notch formula can provide highly accurate results if the flow conditions are well-characterized.
- Cost: The V notch formula can be a cost-effective method for measuring flow rates, especially in small-scale applications.
- Complexity: The V notch formula can be more complex to apply than other methods, especially if the flow conditions are unsteady or turbulent.
Future Developments and Research Directions
There are several future developments and research directions that can improve the accuracy and applicability of the V notch formula. Some key areas of research include:
- Computational fluid dynamics simulations to improve the accuracy of the V notch formula and to validate its results.
- Experimental studies to investigate the effects of turbulence and complex flow patterns on the V notch formula.
- Development of new flow measurement methods that can provide higher accuracy and better reliability than the V notch formula.
How to calculate weir capacity?

To calculate weir capacity, it is essential to understand the principles of fluid dynamics and the characteristics of the weir itself. A weir is a type of barrier or obstruction in a watercourse that alters the flow of water, and its capacity is determined by the amount of water that can flow over or through it. The calculation of weir capacity involves several factors, including the height of the weir, the length of the weir, and the type of weir.
Introduction to Weir Capacity Calculation
The calculation of weir capacity is crucial in various fields, such as hydrology, civil engineering, and water resources management. To calculate weir capacity, one needs to consider the flow rate of the water, the weir shape, and the water level upstream and downstream of the weir. The following steps can be taken to calculate weir capacity:
- Determine the weir type, such as a sharp-crested weir or a broad-crested weir
- Measure the weir height and length
- Calculate the flow rate of the water using the velocity and cross-sectional area of the watercourse
Factors Affecting Weir Capacity
Several factors can affect the capacity of a weir, including the weir material, the water viscosity, and the air resistance. The shape and size of the weir also play a significant role in determining its capacity. For example, a sharp-crested weir has a different capacity than a broad-crested weir due to the differences in their shapes and flow characteristics. The following factors can influence weir capacity:
- Water density and viscosity
- Weir shape and size
- Air resistance and frictional losses
Weir Capacity Calculation Methods
There are several methods to calculate weir capacity, including the Francis formula, the Bazin formula, and the Rehbock formula. Each method has its advantages and disadvantages, and the choice of method depends on the specific conditions of the weir and the watercourse. The following methods can be used to calculate weir capacity:
- The Francis formula, which is suitable for sharp-crested weirs
- The Bazin formula, which is suitable for broad-crested weirs
- The Rehbock formula, which is suitable for weirs with complex shapes
Applications of Weir Capacity Calculation
The calculation of weir capacity has several practical applications, including the design of irrigation systems, flood control structures, and hydroelectric power plants. Accurate calculation of weir capacity is essential to ensure the safe and efficient operation of these systems. The following applications require the calculation of weir capacity:
- Irrigation system design to ensure adequate water supply
- Flood control structure design to prevent flooding and erosion
- Hydroelectric power plant design to optimize energy production
Limitations and Challenges of Weir Capacity Calculation
Despite the importance of weir capacity calculation, there are several limiting factors and challenges associated with it, including the complexity of the flow equations and the uncertainty of the input parameters. Additionally, the accuracy of the calculation depends on the quality of the input data and the simplifications made in the calculation process. The following limitations and challenges can affect weir capacity calculation:
- Complexity of flow equations and non-linear relationships
- Uncertainty of input parameters and measurement errors
- Limitations of calculation methods and simplifications
What is the discharge coefficient of a triangular weir?

The discharge coefficient of a triangular weir is a dimensionless value that represents the ratio of the actual flow rate to the theoretical flow rate over the weir. It is an important parameter in hydraulic engineering and is used to calculate the flow rate of water over a triangular weir. The discharge coefficient is affected by various factors, including the weir geometry, water level, and flow conditions.
Introduction to Triangular Weirs
Triangular weirs are a type of sharp-crested weir that is commonly used in water resources engineering to measure flow rates. The discharge coefficient of a triangular weir is typically in the range of 0.5 to 0.6, depending on the weir design and flow conditions. The discharge coefficient is an important parameter in the design and operation of water supply systems, wastewater treatment plants, and hydroelectric power plants. The following are some key factors that affect the discharge coefficient of a triangular weir:
- The weir angle and crest width can affect the discharge coefficient, with narrower crests and smaller angles resulting in higher discharge coefficients.
- The water level above the weir crest can also affect the discharge coefficient, with higher water levels resulting in higher discharge coefficients.
- The flow velocity and turbulence can also impact the discharge coefficient, with higher flow velocities and turbulence resulting in lower discharge coefficients.
Factors Affecting Discharge Coefficient
The discharge coefficient of a triangular weir is affected by various factors, including the weir geometry, water level, and flow conditions. The weir angle and crest width can affect the discharge coefficient, with narrower crests and smaller angles resulting in higher discharge coefficients. The water level above the weir crest can also affect the discharge coefficient, with higher water levels resulting in higher discharge coefficients. The following are some key factors that can affect the discharge coefficient:
- The weir material and surface roughness can affect the discharge coefficient, with smoother surfaces resulting in higher discharge coefficients.
- The water temperature and viscosity can also impact the discharge coefficient, with higher temperatures and lower viscosities resulting in higher discharge coefficients.
- The flow regime and turbulence can also affect the discharge coefficient, with more turbulent flows resulting in lower discharge coefficients.
Calculation of Discharge Coefficient
The discharge coefficient of a triangular weir can be calculated using various empirical formulas and theoretical models. The most common method is to use the Bazin formula, which is based on the weir geometry and water level. The formula is: Cd = 0.544 + 0.0415(H/P), where Cd is the discharge coefficient, H is the water level above the weir crest, and P is the weir crest width. The following are some key steps in calculating the discharge coefficient:
- Measure the weir geometry, including the weir angle and crest width.
- Measure the water level above the weir crest.
- Calculate the discharge coefficient using the Bazin formula or other empirical formulas.
Applications of Triangular Weirs
Triangular weirs are widely used in water resources engineering to measure flow rates and calculate discharge coefficients. They are commonly used in water supply systems, wastewater treatment plants, and hydroelectric power plants. The discharge coefficient of a triangular weir is an important parameter in the design and operation of these systems. The following are some key applications of triangular weirs:
- Flow measurement: Triangular weirs can be used to measure flow rates in open channels and pipelines.
- Water supply systems: Triangular weirs can be used to regulate flow rates and calculate discharge coefficients in water supply systems.
- Wastewater treatment plants: Triangular weirs can be used to measure flow rates and calculate discharge coefficients in wastewater treatment plants.
Limitations and Uncertainties
The discharge coefficient of a triangular weir is subject to various limitiations and uncertainties, including weir geometry, water level, and flow conditions. The discharge coefficient can be affected by scale effects, modeling errors, and measurement uncertainties. The following are some key limitations and uncertainties:
- Scale effects: The discharge coefficient can be affected by scale effects, including the weir size and water level.
- Modeling errors: The discharge coefficient can be affected by modeling errors, including the empirical formulas and theoretical models used to calculate the discharge coefficient.
- Measurement uncertainties: The discharge coefficient can be affected by measurement uncertainties, including the water level and flow velocity measurements.
What is the formula for weir overflow rate?
The formula for weir overflow rate is given by the equation: Q = (2/3) C L H^(3/2), where Q is the flow rate, C is the weir coefficient, L is the length of the weir, and H is the height of the water above the weir crest.
Understanding Weir Overflow Rate
The weir overflow rate is a measure of the flow rate of water over a weir, which is a barrier or obstruction in a water flow path. The weir overflow rate is an important parameter in the design of water treatment plants, reservoirs, and dams. To calculate the weir overflow rate, the following steps can be taken:
- Measure the length of the weir (L) and the height of the water above the weir crest (H)
- Determine the weir coefficient (C) based on the type of weir and the water flow conditions
- Use the formula Q = (2/3) C L H^(3/2) to calculate the flow rate (Q)
Factors Affecting Weir Overflow Rate
The weir overflow rate is affected by several factors, including the weir coefficient, the length of the weir, and the height of the water above the weir crest. Other factors that can affect the weir overflow rate include the water flow velocity, the water level, and the presence of obstructions or debris in the water flow path. The following factors can influence the weir overflow rate:
- Water flow velocity: An increase in water flow velocity can increase the weir overflow rate
- Water level: An increase in water level can increase the weir overflow rate
- Obstructions or debris: The presence of obstructions or debris can decrease the weir overflow rate
Types of Weirs
There are several types of weirs, including sharp-crested weirs, broad-crested weirs, and vegetated weirs. Each type of weir has a different weir coefficient and is affected by different factors. The following are some common types of weirs:
- Sharp-crested weirs: These weirs have a sharp crest and are commonly used in water treatment plants and reservoirs
- Broad-crested weirs: These weirs have a broad crest and are commonly used in dams and flood control structures
- Vegetated weirs: These weirs are covered with vegetation and are commonly used in wetlands and ecological restoration projects
Applications of Weir Overflow Rate
The weir overflow rate has several applications in civil engineering, environmental engineering, and ecology. The weir overflow rate is used to design water treatment plants, reservoirs, and dams, and to predict the water flow and water level in rivers and streams. The following are some applications of the weir overflow rate:
- Water treatment plant design: The weir overflow rate is used to design water treatment plants and to predict the water flow and water level in the plant
- Reservoir design: The weir overflow rate is used to design reservoirs and to predict the water flow and water level in the reservoir
- Flood control: The weir overflow rate is used to predict the water flow and water level in rivers and streams and to design flood control structures
Limitations of Weir Overflow Rate
The weir overflow rate has several limitations, including the assumption of a steady-state flow and the neglect of turbulence and friction. The weir overflow rate is also affected by the weir coefficient, which can be difficult to determine accurately. The following are some limitations of the weir overflow rate:
- Assumption of steady-state flow: The weir overflow rate assumes a steady-state flow, which may not always be the case in reality
- Neglect of turbulence and friction: The weir overflow rate neglects turbulence and friction, which can affect the water flow and water level
- Difficulty in determining the weir coefficient: The weir coefficient can be difficult to determine accurately, which can affect the accuracy of the weir overflow rate
Frequently Asked Questions (FAQs)
What is the Triangular Weirs Flow Formula and how is it used in calculations?
The Triangular Weirs Flow Formula is a mathematical equation used to calculate the flow rate of fluids, such as water, through a triangular weir. A triangular weir is a type of weir that has a triangular shape, with the upstream face being vertical and the downstream face being inclined. The formula is based on the principle of conservation of energy and takes into account the head of the fluid, the angle of the weir, and the discharge coefficient. The formula is widely used in hydrology and hydraulics to calculate the flow rate of rivers, streams, and canals, and is an essential tool for engineers and researchers working in these fields. The Triangular Weirs Flow Formula is a complex equation that requires a good understanding of mathematics and physics, as well as a thorough knowledge of the properties of fluids.
How does the Triangular Weirs Flow Calculator work and what are its limitations?
The Triangular Weirs Flow Calculator is a software tool that uses the Triangular Weirs Flow Formula to calculate the flow rate of fluids through a triangular weir. The calculator takes into account the input parameters such as the head of the fluid, the angle of the weir, and the discharge coefficient, and uses these values to calculate the flow rate. The calculator is designed to be user-friendly and easy to use, with a simple interface that allows users to input the required parameters and obtain the calculated flow rate. However, the calculator has several limitations, including the assumption that the fluid is incompressible and that the flow is steady and uniform. Additionally, the calculator may not account for friction losses or turbulence, which can affect the accuracy of the calculated flow rate. Therefore, users should be aware of these limitations and use the calculator with caution, and only after thoroughly understanding the underlying mathematics and physics.
What are the advantages and disadvantages of using the Triangular Weirs Flow Formula and Calculator?
The Triangular Weirs Flow Formula and Calculator have several advantages, including their ability to provide accurate calculations of the flow rate of fluids through triangular weirs. The formula and calculator are also widely used in hydrology and hydraulics, and are accepted as a standard method for calculating flow rates. Additionally, the calculator is easy to use and requires minimal input parameters, making it a convenient tool for engineers and researchers. However, there are also several disadvantages to using the Triangular Weirs Flow Formula and Calculator, including the assumptions made about the fluid and the flow, which may not always be valid. The calculator may also not account for friction losses or turbulence, which can affect the accuracy of the calculated flow rate. Furthermore, the formula and calculator are only applicable to triangular weirs, and may not be suitable for other types of weirs or flow measurement devices. Therefore, users should carefully consider the advantages and disadvantages before using the Triangular Weirs Flow Formula and Calculator.
How can the Triangular Weirs Flow Formula and Calculator be applied in real-world scenarios and what are the potential applications?
The Triangular Weirs Flow Formula and Calculator can be applied in a variety of real-world scenarios, including the measurement of flow rates in rivers, streams, and canals. The formula and calculator can also be used to design and optimize irrigation systems, water supply systems, and wastewater treatment systems. Additionally, the formula and calculator can be used to study hydrological and hydraulic phenomena, such as floods and droughts, and to develop models and simulations of water flow. The potential applications of the Triangular Weirs Flow Formula and Calculator are numerous and diverse, and include agriculture, urban planning, environmental engineering, and research. The formula and calculator can also be used to develop new technologies and innovations, such as advanced water management systems and sustainable water resources. Overall, the Triangular Weirs Flow Formula and Calculator are powerful tools that can be used to improve our understanding of water flow and to develop more efficient and sustainable water management systems.
Deja una respuesta

Entradas Relacionadas