Thin-Walled Cylinders Internal Pressure Formula and Calculator

The internal pressure of a thin-walled cylinder is a critical factor in determining its structural integrity. When a cylinder is subjected to internal pressure, it can lead to stress and potential failure. The formula for calculating the internal pressure of a thin-walled cylinder is based on the principles of mechanics of materials. This article provides a comprehensive overview of the internal pressure formula and offers a calculator to help engineers and designers determine the maximum allowable pressure for a given cylinder. The calculator takes into account the cylinder's dimensions and material properties.
- Understanding Thin-Walled Cylinders Internal Pressure Formula and Calculator
- What is the internal pressure of a thin cylinder?
- What is the formula for the internal pressure cylinder?
- What is the formula for calculating the bursting pressure of a thin walled cylinder?
- What is the lame equation for a thin walled cylinder?
-
Frequently Asked Questions (FAQs)
- What is the Thin-Walled Cylinders Internal Pressure Formula and how is it used?
- How does the Thin-Walled Cylinders Internal Pressure Calculator work?
- What are the limitations and assumptions of the Thin-Walled Cylinders Internal Pressure Formula?
- How can I use the Thin-Walled Cylinders Internal Pressure Formula and Calculator in my engineering design work?
Understanding Thin-Walled Cylinders Internal Pressure Formula and Calculator
The internal pressure of a thin-walled cylinder is a critical parameter in various engineering applications, including piping systems, tanks, and pressure vessels. The formula used to calculate the internal pressure of a thin-walled cylinder is based on the stress and strain principles of mechanics of materials. The calculator for internal pressure is a useful tool for engineers to quickly and accurately determine the pressure that a cylinder can withstand without failing.
Introduction to Thin-Walled Cylinders
Thin-walled cylinders are cylindrical vessels with a wall thickness that is relatively small compared to the diameter of the cylinder. The internal pressure of a thin-walled cylinder is determined by the stress and strain principles, which are based on the material properties of the cylinder. The formula for calculating the internal pressure of a thin-walled cylinder is: P = (2 σ t) / r, where P is the internal pressure, σ is the allowable stress, t is the wall thickness, and r is the radius of the cylinder.
Formula for Internal Pressure Calculation
The formula for calculating the internal pressure of a thin-walled cylinder is: P = (2 σ t) / r. This formula is based on the stress and strain principles of mechanics of materials. The formula takes into account the material properties of the cylinder, such as the allowable stress and the wall thickness. The calculator for internal pressure uses this formula to quickly and accurately determine the pressure that a cylinder can withstand without failing.
Calculator for Internal Pressure
A calculator for internal pressure is a useful tool for engineers to quickly and accurately determine the pressure that a cylinder can withstand without failing. The calculator uses the formula for calculating the internal pressure of a thin-walled cylinder, which is: P = (2 σ t) / r. The calculator requires input values for the allowable stress, wall thickness, and radius of the cylinder. The calculator then uses these values to calculate the internal pressure of the cylinder.
Material Properties and Internal Pressure
The material properties of a cylinder play a critical role in determining the internal pressure that it can withstand. The allowable stress of the material is a key factor in determining the internal pressure. The allowable stress is the maximum stress that a material can withstand without failing. Other material properties, such as the yield strength and ultimate strength, also affect the internal pressure of a cylinder.
Applications of Thin-Walled Cylinders
Thin-walled cylinders have a wide range of applications in various industries, including piping systems, tanks, and pressure vessels. The internal pressure of a thin-walled cylinder is a critical parameter in these applications. The formula and calculator for internal pressure are useful tools for engineers to quickly and accurately determine the pressure that a cylinder can withstand without failing.
| Parameter | Unit | Description |
|---|---|---|
| Internal Pressure | psi | The pressure inside the cylinder |
| Allowable Stress | psi | The maximum stress that the material can withstand |
| Wall Thickness | in | The thickness of the cylinder wall |
| Radius | in | The radius of the cylinder |
What is the internal pressure of a thin cylinder?
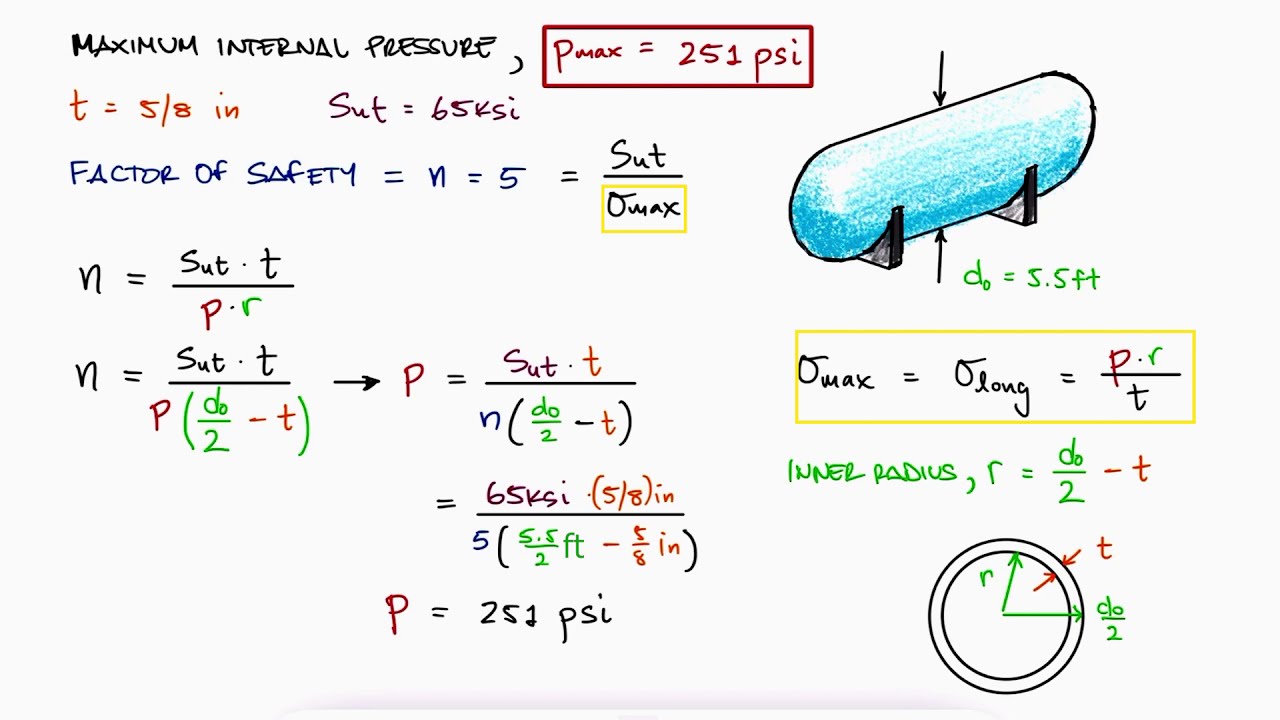
The internal pressure of a thin cylinder is determined by the stress and strain on the material due to the internal forces acting on it. This pressure is a critical factor in the design and construction of cylindrical structures, such as pipes, tanks, and pressure vessels. The internal pressure of a thin cylinder can be calculated using the Lame's equation, which takes into account the hoop stress and longitudinal stress on the cylinder.
Calculation of Internal Pressure
The calculation of internal pressure in a thin cylinder involves the use of formulas and equations that consider the geometry and material properties of the cylinder. The internal pressure can be calculated using the following steps:
- Determine the radius and thickness of the cylinder
- Calculate the hoop stress and longitudinal stress on the cylinder using Lame's equation
- Use the stress and strain values to calculate the internal pressure
Factors Affecting Internal Pressure
The internal pressure of a thin cylinder is affected by several factors, including the material properties, geometry, and operating conditions. The temperature and pressure of the fluid inside the cylinder can also impact the internal pressure. Additionally, the corrosion and wear of the cylinder material can reduce its strength and increase the internal pressure.
Design Considerations
The design of a thin cylinder must take into account the internal pressure and the resulting stresses on the material. The wall thickness and material selection are critical factors in determining the safety and reliability of the cylinder. The designer must also consider the fabrication and installation of the cylinder, as well as the maintenance and inspection requirements.
Applications of Thin Cylinders
Thin cylinders are used in a wide range of applications, including pipelines, pressurized tanks, and pressure vessels. These cylinders are often used in industrial and commercial settings, such as chemical plants, oil refineries, and power generation facilities. The internal pressure of the cylinder is a critical factor in ensuring the safe and efficient operation of these systems.
Material Selection
The material selection for a thin cylinder is critical in determining its strength, durability, and resistance to corrosion and wear. The mechanical properties of the material, such as its yield strength and ultimate strength, are important factors in selecting the right material for the application. The designer must also consider the cost, availability, and fabrication requirements of the material, as well as its compatibility with the fluid or gas being transported.
What is the formula for the internal pressure cylinder?

The formula for the internal pressure of a cylinder is given by the Laplace's law, which states that the pressure difference across a curved surface is proportional to the tension in the surface and inversely proportional to the radius of curvature. Mathematically, this can be expressed as: P = 2T/r, where P is the pressure difference, T is the tension in the surface, and r is the radius of curvature.
Understanding the Concept of Internal Pressure
The concept of internal pressure in a cylinder is crucial in understanding various engineering applications, such as piping systems and pressure vessels. The internal pressure of a cylinder is the pressure exerted by the fluid inside the cylinder on its walls. This pressure can be calculated using the formula: P = (2 T) / r, where T is the tension in the surface and r is the radius of the cylinder. Some key points to consider when calculating internal pressure are:
- The material properties of the cylinder, such as its elastic modulus and Poisson's ratio
- The geometric parameters of the cylinder, such as its radius and length
- The boundary conditions of the cylinder, such as the pressure and temperature at the edges
Factors Affecting Internal Pressure
The internal pressure of a cylinder is affected by several factors, including the size and shape of the cylinder, the properties of the fluid inside, and the external loads applied to the cylinder. The size of the cylinder, in particular, plays a crucial role in determining the internal pressure, as larger cylinders tend to have lower internal pressures due to the increased volume of the fluid. Some key factors that affect internal pressure are:
- The density of the fluid inside the cylinder
- The viscosity of the fluid inside the cylinder
- The surface roughness of the cylinder
Calculating Internal Pressure using Laplace's Law
Laplace's law can be used to calculate the internal pressure of a cylinder by considering the tension in the surface and the radius of curvature. The law states that the pressure difference across a curved surface is proportional to the tension in the surface and inversely proportional to the radius of curvature. This can be expressed mathematically as: P = 2T/r, where P is the pressure difference, T is the tension in the surface, and r is the radius of curvature. Some key steps to calculate internal pressure using Laplace's law are:
- Calculate the tension in the surface of the cylinder
- Calculate the radius of curvature of the cylinder
- Apply Laplace's law to calculate the internal pressure
Applications of Internal Pressure in Engineering
The concept of internal pressure is crucial in various engineering applications, such as piping systems, pressure vessels, and boilers. The internal pressure of a! cylinder is used to design and analyze these systems, ensuring that they can withstand the stresses and strains caused by the internal pressure. Some key applications of internal pressure in engineering are:
- Piping systems: designing pipes to withstand internal pressure and external loads
- Pressure vessels: designing vessels to withstand internal pressure and external loads
- Boilers: designing boilers to withstand internal pressure and external loads
Importance of Considering Internal Pressure in Design
Considering internal pressure is crucial in the design and analysis of cylindrical structures, such as pipes and pressure vessels. The internal pressure can cause stresses and strains in the material, leading to failure if not properly designed. Some key reasons why considering internal pressure is important in design are:
- Safety: ensuring that the structure can withstand the internal pressure and external loads
- Efficiency: optimizing the design to minimize stresses and strains
- Cost: reducing the cost of materials and maintenance by optimizing the design
What is the formula for calculating the bursting pressure of a thin walled cylinder?

The formula for calculating the bursting pressure of a thin-walled cylinder is given by the Lame equation, which is a function of the cylinder's geometry and material properties. The equation is: P = (2 stress thickness) / (radius), where P is the bursting pressure, stress is the hoop stress, thickness is the wall thickness, and radius is the radius of the cylinder.
Factors Affecting Bursting Pressure
The bursting pressure of a thin-walled cylinder is affected by several factors, including the material properties, geometry, and operating conditions. Some of the key factors that influence bursting pressure are:
- Wall thickness: Increasing the wall thickness of the cylinder can significantly increase its bursting pressure.
- Radius: The radius of the cylinder also plays a crucial role in determining its bursting pressure, with larger radii resulting in lower bursting pressures.
- Material strength: The strength and ductility of the material used to manufacture the cylinder can also impact its bursting pressure.
Cylinder Geometry and Bursting Pressure
The geometry of the cylinder, including its length, diameter, and wall thickness, can significantly impact its bursting pressure. For example, a longer cylinder with a larger diameter and thinner walls will have a lower bursting pressure than a shorter cylinder with a smaller diameter and thicker walls. Some of the key geometric factors that influence bursting pressure are:
- Cylinder length: Increasing the length of the cylinder can reduce its bursting pressure due to the increased stress and strain on the material.
- Diameter: The diameter of the cylinder also plays a role in determining its bursting pressure, with larger diameters resulting in lower bursting pressures.
- Wall thickness ratio: The ratio of the wall thickness to the radius of the cylinder can also impact its bursting pressure, with thinner walls resulting in lower bursting pressures.
Material Properties and Bursting Pressure
The material properties of the cylinder, including its strength, ductility, and toughness, can significantly impact its bursting pressure. For example, a cylinder made from a high-strength material with high ductility will have a higher bursting pressure than a cylinder made from a low-strength material with low ductility. Some of the key material properties that influence bursting pressure are:
- Yield strength: The yield strength of the material can impact its bursting pressure, with higher yield strengths resulting in higher bursting pressures.
- Ultimate tensile strength: The ultimate tensile strength of the material can also impact its bursting pressure, with higher ultimate tensile strengths resulting in higher bursting pressures.
- Fracture toughness: The fracture toughness of the material can also influence its bursting pressure, with higher fracture toughness resulting in higher bursting pressures.
Calculating Bursting Pressure using the Lame Equation
The Lame equation can be used to calculate the bursting pressure of a thin-walled cylinder, taking into account the geometry and material properties of the cylinder. The equation is: P = (2 stress thickness) / (radius), where P is the bursting pressure, stress is the hoop stress, thickness is the wall thickness, and radius is the radius of the cylinder. By plugging in the relevant values, engineers can calculate the bursting pressure of the cylinder and determine its safety factor. Some of the key steps involved in calculating bursting pressure using the Lame equation are:
- Determine the hoop stress: The hoop stress can be calculated using the Lame equation, which takes into account the internal pressure and wall thickness of the cylinder.
- Determine the wall thickness: The wall thickness of the cylinder can be measured or calculated using the geometry of the cylinder.
- Determine the radius: The radius of the cylinder can be measured or calculated using the geometry of the cylinder.
Applications of the Lame Equation in Engineering
The Lame equation has numerous applications in engineering, including the design and analysis of pressure vessels, pipelines, and cylindrical containers. By using the Lame equation, engineers can calculate the bursting pressure of a thin-walled cylinder and determine its safety factor, which is critical in ensuring the integrity and reliability of the system. Some of the key applications of the Lame equation are:
- Pressure vessel design: The Lame equation can be used to design pressure vessels that can withstand high pressures and temperatures.
- Pipeline design: The Lame equation can be used to design pipelines that can withstand high pressures and flow rates.
- Cylindrical container design: The Lame equation can be used to design cylindrical containers that can withstand high pressures and temperatures.
What is the lame equation for a thin walled cylinder?
The Lame Equation for a thin-walled cylinder is a mathematical formula used to calculate the stress and strain in a cylindrical vessel under internal pressure. The equation is derived from the theory of elasticity and is a fundamental concept in mechanics of materials. The Lame Equation is given by:
σθ = (p r) / (t 2) + (p r) / (2 t)
where σθ is the hoop stress, p is the internal pressure, r is the radius of the cylinder, and t is the thickness of the cylinder.
Lame Equation Derivation
The Lame Equation is derived from the equilibrium equations and the constitutive equations of the material. The equation is based on the assumption that the cylinder is thin-walled, meaning that the thickness is much smaller than the radius. This assumption allows for the use of the plane stress theory, which simplifies the calculations. The derivation of the Lame Equation involves the following steps:
- Writing the equilibrium equations for the cylinder in terms of the stress components.
- Using the constitutive equations to relate the stress components to the strain components.
- Applying the boundary conditions to the cylinder, including the internal pressure and the external pressure.
Assumptions of the Lame Equation
The Lame Equation is based on several assumptions that simplify the calculations and make the equation applicable to a wide range of problems. These assumptions include:
- The cylinder is thin-walled, meaning that the thickness is much smaller than the radius.
- The material is isotropic, meaning that its mechanical properties are the same in all directions.
- The internal pressure is uniform and does not vary with time or position.
These assumptions allow for the use of the plane stress theory and simplify the calculations, but they also limit the applicability of the Lame Equation to certain types of problems.
Limitations of the Lame Equation
The Lame Equation has several limitations that must be considered when applying it to real-world problems. These limitations include:
- The equation is only applicable to thin-walled cylinders, and is not suitable for thick-walled cylinders.
- The equation assumes that the internal pressure is uniform, and does not account for pressure gradients or non-uniform loading.
- The equation is based on the theory of elasticity, and does not account for plastic deformation or failure.
These limitations mean that the Lame Equation must be used with caution and only applied to problems where the assumptions are valid.
Applications of the Lame Equation
The Lame Equation has a wide range of applications in engineering and physics, including:
- Pressure vessel design, where the equation is used to calculate the stress and strain in cylindrical vessels.
- Piping systems, where the equation is used to calculate the stress and strain in pipes under internal pressure.
- Mechanical engineering, where the equation is used to calculate the stress and strain in machine components.
These applications demonstrate the importance of the Lame Equation in engineering and physics, and highlight its usefulness in a wide range of problems.
Comparison with Other Equations
The Lame Equation can be compared to other equations used to calculate the stress and strain in cylindrical vessels, such as the Barlow Equation and the Bourke Equation. These equations are similar to the Lame Equation, but are based on different assumptions and are applicable to different types of problems. The Lame Equation is generally more conservative than the other equations, meaning that it predicts higher stresses and strains for a given internal pressure. This makes it a useful design equation for pressure vessel design and other engineering applications.
- The Barlow Equation is a simplified version of the Lame Equation, and is often used for quick estimates.
- The Bourke Equation is a more complex equation that accounts for non-uniform loading and pressure gradients.
- The Lame Equation is a fundamental equation that is widely used in engineering and physics.
These equations demonstrate the importance of the Lame Equation in engineering and physics, and highlight its usefulness in a wide range of problems. The stress and strain calculated using the Lame Equation are critical in designing safe and reliable pressure vessels and machine components.
Frequently Asked Questions (FAQs)
What is the Thin-Walled Cylinders Internal Pressure Formula and how is it used?
The Thin-Walled Cylinders Internal Pressure Formula is a mathematical equation used to calculate the stress and strain on a thin-walled cylinder due to internal pressure. The formula is given by: σ = (P r) / t, where σ is the hoop stress, P is the internal pressure, r is the radius of the cylinder, and t is the thickness of the cylinder wall. This formula is commonly used in engineering and design applications to determine the safety factor and structural integrity of thin-walled cylinders subjected to internal pressure. The thin-walled cylinder is a type of pressure vessel that is commonly used in industrial and aerospace applications, such as pipelines, tanks, and rocket fuel tanks. The internal pressure can cause stress and strain on the cylinder wall, which can lead to failure if not properly designed and analyzed.
How does the Thin-Walled Cylinders Internal Pressure Calculator work?
The Thin-Walled Cylinders Internal Pressure Calculator is a software tool that uses the Thin-Walled Cylinders Internal Pressure Formula to calculate the stress and strain on a thin-walled cylinder due to internal pressure. The calculator takes into account the input parameters such as the internal pressure, radius, and thickness of the cylinder, and uses the formula to calculate the hoop stress and other stresses. The calculator can also be used to calculate the required thickness of the cylinder wall to withstand a given internal pressure, or to calculate the maximum internal pressure that a cylinder can withstand with a given wall thickness. The calculator is user-friendly and can be used by engineers and designers to quickly and accurately calculate the stress and strain on thin-walled cylinders.
What are the limitations and assumptions of the Thin-Walled Cylinders Internal Pressure Formula?
The Thin-Walled Cylinders Internal Pressure Formula is based on several assumptions and limitations, including the assumption that the cylinder wall is thin compared to the radius, and that the internal pressure is uniform and constant. The formula also assumes that the material of the cylinder is isotropic and homogeneous, and that the stress and strain are within the elastic limit of the material. Additionally, the formula does not take into account other loads such as axial loads, bending moments, and torque, which can also cause stress and strain on the cylinder. The formula is also based on a simplified analysis of the stress and strain on the cylinder, and does not take into account complex phenomena such as plasticity and creep.
How can I use the Thin-Walled Cylinders Internal Pressure Formula and Calculator in my engineering design work?
The Thin-Walled Cylinders Internal Pressure Formula and Calculator can be used in a variety of engineering design applications, including the design of pipelines, tanks, and pressure vessels. The formula and calculator can be used to calculate the required thickness of the cylinder wall to withstand a given internal pressure, or to calculate the maximum internal pressure that a cylinder can withstand with a given wall thickness. The formula and calculator can also be used to optimize the design of thin-walled cylinders by minimizing the weight and cost while maintaining structural integrity and safety. Additionally, the formula and calculator can be used to analyze and evaluate the stress and strain on existing cylinders and pressure vessels, and to identify potential failure modes and design flaws. By using the Thin-Walled Cylinders Internal Pressure Formula and Calculator, engineers and designers can ensure that their designs are safe, reliable, and efficient, and that they meet the requirements and standards of the industry.
Deja una respuesta


Entradas Relacionadas