Sphere Surface Drag Drag Coefficient Equation and Calculator
The drag coefficient is a crucial factor in understanding the interaction between a sphere and the surrounding fluid, such as air or water. It is a dimensionless quantity that represents the ratio of the drag force to the inertia force. The sphere surface drag coefficient equation is used to calculate this coefficient, taking into account the velocity, density, and viscosity of the fluid, as well as the diameter of the sphere. This article will explore the equation and provide a calculator to determine the drag coefficient for various spheres and flow conditions. Accurate calculations are essential.
- Sphere Surface Drag Drag Coefficient Equation and Calculator
- What is the formula for the drag coefficient of a sphere?
- What is the Reynolds number equation for a sphere?
- How does CFD calculate drag coefficient?
- How do you calculate the drag of a cylinder?
-
Frequently Asked Questions (FAQs)
- What is the significance of the Sphere Surface Drag Coefficient Equation in fluid dynamics?
- How does the Sphere Surface Drag Coefficient Equation relate to the Calculator?
- What are the key assumptions and limitations of the Sphere Surface Drag Coefficient Equation?
- How can the Sphere Surface Drag Coefficient Equation be applied in real-world scenarios?
Sphere Surface Drag Drag Coefficient Equation and Calculator
The Sphere Surface Drag is a critical aspect of understanding the behavior of objects in fluid dynamics. The Drag Coefficient is a dimensionless quantity that characterizes the amount of drag exerted on an object by a fluid, such as air or water. In the case of a sphere, the drag coefficient is a function of the Reynolds Number, which is defined as the ratio of inertial forces to viscous forces. The Equation for calculating the drag coefficient of a sphere is typically given by the formula: CD = 24/Re + 6/(1 + √Re) + 0.4, where CD is the drag coefficient and Re is the Reynolds number.
Introduction to Sphere Surface Drag
The study of Sphere Surface Drag is essential in various fields, including engineering, physics, and mathematics. It helps in understanding how objects move through fluids and how to minimize or maximize the drag forces. The Drag Coefficient Equation is a fundamental tool in this study, as it provides a mathematical representation of the relationship between the drag force and the properties of the fluid and the object. By understanding this equation, researchers and engineers can design more efficient systems, such as wind turbines, aircraft, and submarines.
Reynolds Number and its Significance
The Reynolds Number is a crucial parameter in fluid dynamics, as it determines the nature of the fluid flow. It is defined as the ratio of inertial forces to viscous forces and is given by the formula: Re = ρUL/μ, where ρ is the density of the fluid, U is the velocity of the object, L is the characteristic length of the object, and μ is the dynamic viscosity of the fluid. The Reynolds number is significant because it helps in predicting the type of flow that will occur around an object. For example, a low Reynolds number indicates laminar flow, while a high Reynolds number indicates turbulent flow.
Calculation of Drag Coefficient
The calculation of the Drag Coefficient involves using the equation: CD = 24/Re + 6/(1 + √Re) + 0.4. This equation is valid for a wide range of Reynolds numbers and provides a good approximation of the drag coefficient. However, it is essential to note that the drag coefficient can vary depending on the specific conditions of the flow. For example, the presence of turbulence or the use of a non-spherical object can affect the drag coefficient. To calculate the drag coefficient, one needs to know the Reynolds Number, which can be calculated using the formula: Re = ρUL/μ.
Applications of Sphere Surface Drag
The study of Sphere Surface Drag has numerous applications in various fields. For example, in the design of wind turbines, understanding the drag forces on the blades is crucial in optimizing their performance. Similarly, in the design of aircraft, minimizing the drag forces can help in reducing fuel consumption and increasing efficiency. Additionally, the study of sphere surface drag is essential in the design of submarines, where minimizing the drag forces can help in increasing their speed and maneuverability.
Drag Coefficient Calculator
A Drag Coefficient Calculator is a tool that can be used to calculate the drag coefficient of an object. The calculator typically requires the input of the Reynolds Number and the density and viscosity of the fluid. The calculator then uses the equation: CD = 24/Re + 6/(1 + √Re) + 0.4 to calculate the drag coefficient. The calculator can be a useful tool for engineers and researchers who need to quickly calculate the drag coefficient of an object.
| Reynolds Number | Density | Viscosity | Drag Coefficient |
|---|---|---|---|
| 100 | 1.2 kg/m³ | 1.8 x 10⁻⁵ Pa·s | 0.47 |
| 1000 | 1.2 kg/m³ | 1.8 x 10⁻⁵ Pa·s | 0.27 |
| 10000 | 1.2 kg/m³ | 1.8 x 10⁻⁵ Pa·s | 0.17 |
What is the formula for the drag coefficient of a sphere?
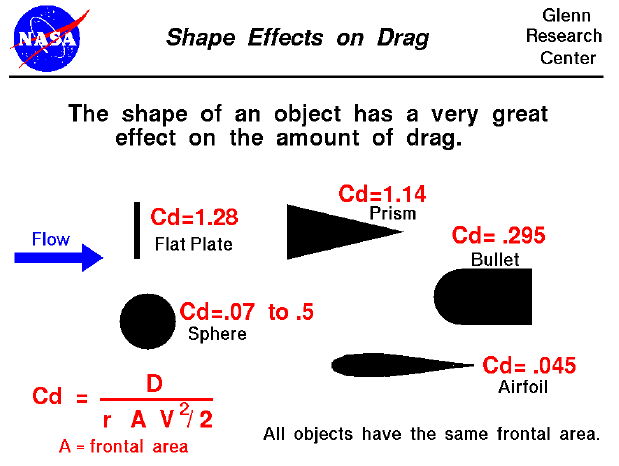
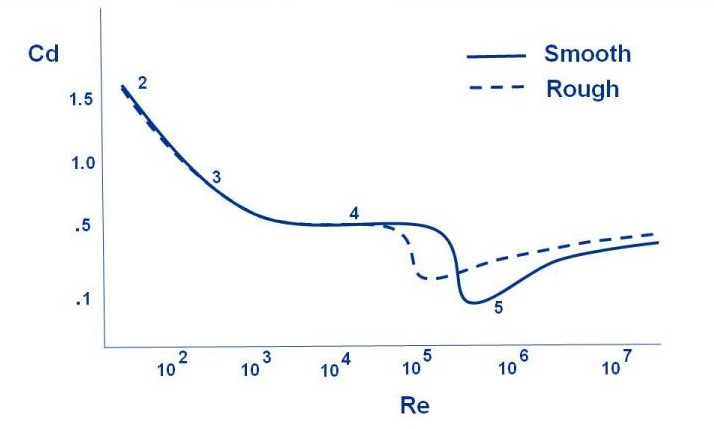
The formula for the drag coefficient of a sphere is given by the equation: Cd = 24/Re + 6/(1 + √Re) + 0.4, where Cd is the drag coefficient, Re is the Reynolds number, which is a dimensionless quantity used to predict flow patterns in different fluid flow situations. The Reynolds number is defined as the ratio of inertial forces to viscous forces and is given by the equation: Re = ρUL/μ, where ρ is the fluid density, U is the fluid velocity, L is the characteristic length, and μ is the fluid viscosity.
Introduction to Drag Coefficient
The drag coefficient is a dimensionless quantity that is used to quantify the amount of drag force that acts on an object as it moves through a fluid. The drag coefficient is an important parameter in the design of vehicles, aircraft, and other objects that move through fluids. The drag coefficient is calculated using the equation: Cd = 2Fd / (ρU^2A), where Fd is the drag force, ρ is the fluid density, U is the fluid velocity, and A is the cross-sectional area of the object.
- The drag coefficient is affected by the shape and size of the object.
- The drag coefficient is also affected by the velocity and density of the fluid.
- The drag coefficient is an important parameter in the design of vehicles and aircraft.
Reynolds Number and Drag Coefficient
The Reynolds number is a dimensionless quantity that is used to predict flow patterns in different fluid flow situations. The Reynolds number is calculated using the equation: Re = ρUL/μ, where ρ is the fluid density, U is the fluid velocity, L is the characteristic length, and μ is the fluid viscosity. The Reynolds number is an important parameter in the calculation of the drag coefficient.
- The Reynolds number is used to predict the transition from laminar to turbulent flow.
- The Reynolds number is affected by the velocity and density of the fluid.
- The Reynolds number is an important parameter in the design of vehicles and aircraft.
Factors Affecting Drag Coefficient
The drag coefficient is affected by several factors, including the shape and size of the object, the velocity and density of the fluid, and the surface roughness of the object. The drag coefficient is also affected by the Reynolds number, which is a dimensionless quantity used to predict flow patterns in different fluid flow situations.
- The shape and size of the object affect the drag coefficient.
- The velocity and density of the fluid affect the drag coefficient.
- The surface roughness of the object affects the drag coefficient.
Calculation of Drag Coefficient
The drag coefficient is calculated using the equation: Cd = 2Fd / (ρU^2A), where Fd is the drag force, ρ is the fluid density, U is the fluid velocity, and A is the cross-sectional area of the object. The drag coefficient is an important parameter in the design of vehicles, aircraft, and other objects that move through fluids.
- The drag coefficient is calculated using the drag force and fluid velocity.
- The drag coefficient is affected by the fluid density and cross-sectional area.
- The drag coefficient is an important parameter in the design of vehicles and aircraft.
Applications of Drag Coefficient
The drag coefficient has several applications in the design of vehicles, aircraft, and other objects that move through fluids. The drag coefficient is used to predict the drag force that acts on an object as it moves through a fluid. The drag coefficient is also used to optimize the shape and size of objects to minimize drag and maximize efficiency.
- The drag coefficient is used to predict the drag force that acts on an object.
- The drag coefficient is used to optimize the shape and size of objects.
- The drag coefficient is an important parameter in the design of vehicles and aircraft.
What is the Reynolds number equation for a sphere?
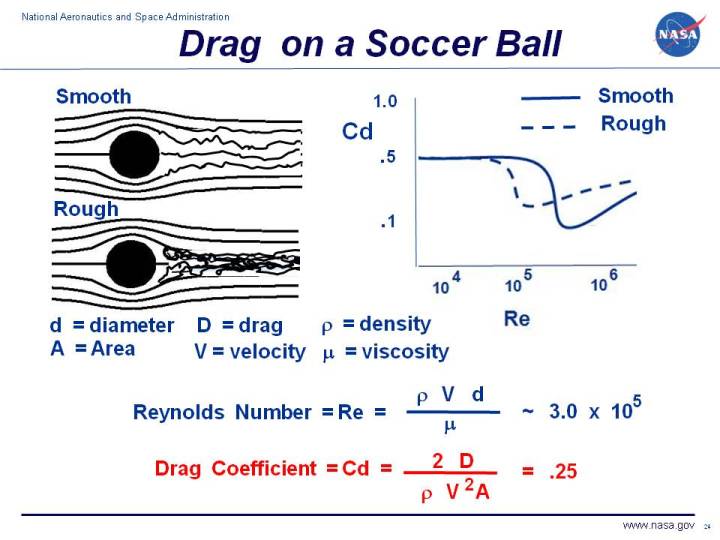
The Reynolds number equation for a sphere is given by the formula: Re = ρUL/μ, where Re is the Reynolds number, ρ is the density of the fluid, U is the velocity of the fluid, L is the diameter of the sphere, and μ is the dynamic viscosity of the fluid. This equation is used to predict the nature of fluid flow around a sphere, whether it is laminar or turbulent.
Introduction to Reynolds Number
The Reynolds number is a dimensionless quantity that is used to predict the nature of fluid flow around an object. It is defined as the ratio of inertial forces to viscous forces in the fluid. The Reynolds number equation for a sphere is an important concept in fluid mechanics and is used in a wide range of applications, including engineering and physics. Some of the key factors that affect the Reynolds number include:
- Velocity of the fluid: The velocity of the fluid has a direct impact on the Reynolds number, with higher velocities resulting in higher Reynolds numbers.
- Density of the fluid: The density of the fluid also affects the Reynolds number, with more dense fluids resulting in higher Reynolds numbers.
- Viscosity of the fluid: The viscosity of the fluid has an inverse impact on the Reynolds number, with more viscous fluids resulting in lower Reynolds numbers.
Importance of Reynolds Number in Fluid Mechanics
The Reynolds number is a crucial concept in fluid mechanics because it allows engineers and physicists to predict the nature of fluid flow around an object. By calculating the Reynolds number, it is possible to determine whether the flow will be laminar or turbulent, which is essential for designing pipes, tanks, and other fluid systems. Some of the key applications of the Reynolds number include:
- Pipe flow: The Reynolds number is used to predict the nature of fluid flow in pipes, which is essential for designing plumbing systems and industrial processes.
- Aerodynamics: The Reynolds number is used to study the behavior of air around objects, such as aircraft and wind turbines.
- Hydrodynamics: The Reynolds number is used to study the behavior of water around objects, such as ships and submarines.
Calculating Reynolds Number for a Sphere
Calculating the Reynolds number for a sphere involves using the formula Re = ρUL/μ, where Re is the Reynolds number, ρ is the density of the fluid, U is the velocity of the fluid, L is the diameter of the sphere, and μ is the dynamic viscosity of the fluid. Some of the key steps involved in calculating the Reynolds number include:
- Measure the diameter of the sphere: The diameter of the sphere is a critical factor in calculating the Reynolds number.
- Measure the velocity of the fluid: The velocity of the fluid is also a critical factor in calculating the Reynolds number.
- Measure the density and viscosity of the fluid: The density and viscosity of the fluid are also important factors in calculating the Reynolds number.
Applications of Reynolds Number in Engineering
The Reynolds number has a wide range of applications in engineering, including aerospace engineering, chemical engineering, and civil engineering. Some of the key applications of the Reynolds number include:
- Designing pipes and tanks: The Reynolds number is used to predict the nature of fluid flow in pipes and tanks, which is essential for designing plumbing systems and industrial processes.
- Designing aircraft and wind turbines: The Reynolds number is used to study the behavior of air around objects, such as aircraft and wind turbines.
- Designing ships and submarines: The Reynolds number is used to study the behavior of water around objects, such as ships and submarines.
Limitations of Reynolds Number
While the Reynolds number is a powerful tool for predicting the nature of fluid flow around an object, it does have some limitations. Some of the key limitations of the Reynolds number include:
- Assumes a spherical shape: The Reynolds number equation for a sphere assumes a spherical shape, which may not always be the case in real-world applications.
- Assumes a uniform velocity: The Reynolds number equation for a sphere assumes a uniform velocity, which may not always be the case in real-world applications.
- Assumes a constant density and viscosity: The Reynolds number equation for a sphere assumes a constant density and viscosity, which may not always be the case in real-world applications.
How does CFD calculate drag coefficient?
The calculation of the drag coefficient using Computational Fluid Dynamics (CFD) involves a complex process that simulates the interaction between a fluid (such as air or water) and an object. This process is based on the Navier-Stokes equations, which describe the motion of fluids and the forces that act upon them. The drag coefficient is a critical parameter in understanding the aerodynamic or hydrodynamic performance of an object, as it affects the force and moment exerted on the object by the fluid.
Simulation Setup
The simulation setup involves creating a virtual model of the object and the surrounding fluid domain. This model is then discretized into smaller elements, and the governing equations are solved for each element. The boundary conditions are applied to the model to represent the interaction between the object and the fluid. The simulation setup is crucial in obtaining accurate results, as it affects the accuracy and efficiency of the calculation. Some key factors to consider in the simulation setup include:
- Mesh quality: The quality of the mesh can significantly affect the accuracy of the results.
- Boundary conditions: The boundary conditions must be carefully chosen to represent the physical problem accurately.
- Turbulence models: The choice of turbulence model can significantly affect the accuracy of the results, especially for turbulent flows.
Grid Generation
The grid generation process involves creating a mesh of elements that discretize the fluid domain and the object. The mesh must be fine enough to capture the details of the flow, but not so fine that it becomes computationally expensive. The grid generation process is critical in obtaining accurate results, as it affects the accuracy and efficiency of the calculation. Some key factors to consider in grid generation include:
- Mesh size: The size of the mesh must be carefully chosen to balance accuracy and computational cost.
- Mesh quality: The quality of the mesh can significantly affect the accuracy of the results.
- Mesh adaptation: The mesh can be adapted to refine or coarsen the mesh in areas of high or low flow gradients.
Fluid Flow Simulation
The fluid flow simulation involves solving the Navier-Stokes equations for the fluid flow around the object. This simulation can be performed using various algorithms, such as the Finite Element Method or the Finite Volume Method. The simulation can be steady-state or transient, depending on the physical problem being modeled. Some key factors to consider in fluid flow simulation include:
- Turbulence models: The choice of turbulence model can significantly affect the accuracy of the results, especially for turbulent flows.
- Viscosity models: The choice of viscosity model can significantly affect the accuracy of the results, especially for non-Newtonian fluids.
- Heat transfer: The simulation can also include heat transfer effects, which can affect the flow and temperature distributions.
Drag Coefficient Calculation
The drag coefficient calculation involves integrating the pressure and viscous forces over the surface of the object. The drag coefficient is a dimensionless quantity that represents the ratio of the drag force to the dynamic pressure. The drag coefficient can be calculated using various methods, such as the integral method or the differential method. Some key factors to consider in drag coefficient calculation include:
- Force calculation: The calculation of the force exerted on the object by the fluid is critical in obtaining accurate results.
- Moment calculation: The calculation of the moment exerted on the object by the fluid is also important, especially for rotating or oscillating objects.
- Surface roughness: The surface roughness of the object can significantly affect the drag coefficient and the flow around the object.
Results Analysis
The results analysis involves visualizing and quantifying the flow and force distributions around the object. The analysis can include contour plots, vector plots, and histograms to visualize the flow and temperature distributions. The results can also be validated against experimental data or other numerical simulations. Some key factors to consider in results analysis include:
- Flow visualization: The visualization of the flow around the object can provide valuable insights into the physics of the problem.
- Force calculation: The calculation of the force exerted on the object by the fluid is critical in obtaining accurate results.
- Sensitivity analysis: The sensitivity of the results to various parameters, such as the mesh size or the turbulence model, can provide valuable insights into the robustness of the simulation.
How do you calculate the drag of a cylinder?

To calculate the drag of a cylinder, you need to consider the shape and size of the cylinder, as well as the velocity and density of the fluid it is moving through. The drag force can be calculated using the drag equation, which takes into account the drag coefficient, the cross-sectional area of the cylinder, and the velocity of the fluid. The drag coefficient is a dimensionless quantity that depends on the shape of the cylinder and the Reynolds number, which is a measure of the turbulence of the fluid.
Understanding the Drag Equation
The drag equation is a mathematical formula that is used to calculate the drag force on an object. It is given by the equation: Fd = ½ ρ v^2 Cd A, where Fd is the drag force, ρ is the density of the fluid, v is the velocity of the fluid, Cd is the drag coefficient, and A is the cross-sectional area of the cylinder. The drag coefficient is a critical component of the drag equation, and it depends on the shape of the cylinder and the Reynolds number. The following are some key factors that affect the drag coefficient:
- The shape of the cylinder, including its length and diameter
- The Reynolds number, which is a measure of the turbulence of the fluid
- The surface roughness of the cylinder, which can affect the drag coefficient
Calculating the Drag Coefficient
The drag coefficient is a dimensionless quantity that depends on the shape of the cylinder and the Reynolds number. It can be calculated using experimental data or numerical simulations. The drag coefficient is typically expressed as a function of the Reynolds number, and it can be affected by the turbulence of the fluid. The following are some key factors that affect the drag coefficient:
- The Reynolds number, which is a measure of the turbulence of the fluid
- The shape of the cylinder, including its length and diameter
- The surface roughness of the cylinder, which can affect the drag coefficient
Effect of Velocity on Drag
The velocity of the fluid has a significant impact on the drag force on a cylinder. As the velocity of the fluid increases, the drag force also increases. This is because the drag equation includes the velocity of the fluid squared, which means that small increases in velocity can result in large increases in drag force. The following are some key factors that affect the velocity of the fluid:
- The density of the fluid, which affects the drag force
- The viscosity of the fluid, which affects the turbulence of the fluid
- The surface roughness of the cylinder, which can affect the drag coefficient
Effect of Density on Drag
The density of the fluid also has a significant impact on the drag force on a cylinder. As the density of the fluid increases, the drag force also increases. This is because the drag equation includes the density of the fluid, which means that small increases in density can result in large increases in drag force. The following are some key factors that affect the density of the fluid:
- The temperature of the fluid, which affects the density
- The pressure of the fluid, which affects the density
- The composition of the fluid, which affects the density
Applications of Drag Calculation
The calculation of drag is critical in a wide range of engineering applications, including the design of aircraft, vehicles, and buildings. It is also important in the optimization of fluid flow systems, such as pipelines and ducts. The following are some key applications of drag calculation:
- The design of aircraft and vehicles, where drag reduction is critical for fuel efficiency
- The design of buildings and bridges, where wind resistance is critical for structural integrity
- The optimization of fluid flow systems, where drag reduction is critical for energy efficiency
Frequently Asked Questions (FAQs)
What is the significance of the Sphere Surface Drag Coefficient Equation in fluid dynamics?
The Sphere Surface Drag Coefficient Equation is a crucial formula in fluid dynamics that helps calculate the drag force exerted on a sphere moving through a fluid, such as air or water. This equation is significant because it allows engineers and researchers to predict the drag coefficient, which is a dimensionless quantity that characterizes the amount of drag experienced by an object. The drag coefficient is influenced by various factors, including the shape and size of the object, as well as the velocity and density of the fluid. By understanding the Sphere Surface Drag Coefficient Equation, scientists can design more efficient systems, such as aircraft and vehicles, that minimize drag and maximize performance.
How does the Sphere Surface Drag Coefficient Equation relate to the Calculator?
The Sphere Surface Drag Coefficient Equation is closely tied to the Calculator, which is a tool used to compute the drag coefficient and other related parameters. The Calculator takes into account various input values, such as the sphere's diameter, fluid density, and velocity, to calculate the drag force and drag coefficient. The equation is implemented in the Calculator using numerical methods, allowing users to obtain accurate results quickly and efficiently. By using the Calculator, engineers and researchers can save time and effort, as they no longer need to manually solve the complex mathematical equations involved in calculating the drag coefficient. The Calculator also provides a user-friendly interface, making it accessible to a wide range of users, from students to professionals.
What are the key assumptions and limitations of the Sphere Surface Drag Coefficient Equation?
The Sphere Surface Drag Coefficient Equation is based on several key assumptions and limitations, which are essential to understand to ensure accurate and reliable results. One of the primary assumptions is that the sphere is perfectly spherical and smooth, with no surface roughness or irregularities. Additionally, the equation assumes that the fluid is incompressible and Newtonian, meaning that its viscosity remains constant. The equation also neglects turbulence and boundary layer effects, which can be significant in certain situations. Furthermore, the Sphere Surface Drag Coefficient Equation is typically valid for laminar flow regimes, where the Reynolds number is relatively low. Users must be aware of these limitations and assumptions to ensure that the equation is applied correctly and that the results are interpreted accurately.
How can the Sphere Surface Drag Coefficient Equation be applied in real-world scenarios?
The Sphere Surface Drag Coefficient Equation has numerous practical applications in various fields, including aerospace engineering, mechanical engineering, and chemical engineering. For example, in aerospace engineering, the equation can be used to design more efficient aircraft and spacecraft by minimizing drag and maximizing lift. In mechanical engineering, the equation can be applied to optimize the performance of pumps, turbines, and other fluid-handling equipment. Additionally, in chemical engineering, the equation can be used to design more efficient chemical reactors and mixing tanks. The Sphere Surface Drag Coefficient Equation can also be used to study environmental phenomena, such as ocean currents and atmospheric circulation patterns. By applying the equation in these contexts, engineers and researchers can gain valuable insights into the behavior of fluids and gases, ultimately leading to improved designs and more efficient systems.
Deja una respuesta

Entradas Relacionadas