Section Modulus S for I Beam Universal Calculator
The Section Modulus S for I Beam Universal Calculator is a versatile tool designed to calculate the section modulus of I-beams, a crucial parameter in structural engineering. The section modulus is a measure of a beam's ability to resist bending and flexure. This calculator provides a universal solution for calculating the section modulus of I-beams with varying dimensions and materials, making it an essential resource for engineers, architects, and construction professionals seeking to ensure the stability and safety of their designs. It offers a convenient and accurate method for calculating section modulus values.
- Section Modulus S for I Beam Universal Calculator
- How to calculate the section modulus of an I beam?
- What is the elastic section modulus of the I section?
- What is the formula for section modulus z?
-
Frequently Asked Questions (FAQs)
- What is the Section Modulus S for I Beam Universal Calculator and how does it work?
- What are the key parameters required to calculate the Section Modulus S for an I Beam?
- How does the Section Modulus S for I Beam Universal Calculator handle different types of loading conditions?
- What are the benefits of using the Section Modulus S for I Beam Universal Calculator in engineering design and analysis?
Section Modulus S for I Beam Universal Calculator
The Section Modulus S for I Beam Universal Calculator is a tool used to calculate the section modulus of I-beams, which is a critical parameter in structural engineering. The section modulus is a measure of the beam's ability to resist bending and is calculated using the beam's cross-sectional area and the distance from the neutral axis to the extreme fiber. The calculator is designed to provide accurate and efficient calculations for a wide range of I-beam shapes and sizes.
Introduction to Section Modulus
The section modulus is a fundamental concept in structural engineering, and it is essential to understand its significance in the design of I-beams. The section modulus is defined as the ratio of the moment of inertia of the beam's cross-section to the distance from the neutral axis to the extreme fiber. It is used to calculate the maximum bending stress in the beam and to determine the beam's ability to resist bending. The section modulus is a critical parameter in the design of I-beams, as it directly affects the beam's structural integrity and stability.
Calculating Section Modulus using the Universal Calculator
The Section Modulus S for I Beam Universal Calculator is a powerful tool that allows users to calculate the section modulus of I-beams quickly and accurately. The calculator takes into account the beam's cross-sectional area, the distance from the neutral axis to the extreme fiber, and other relevant parameters to calculate the section modulus. The calculator is designed to be user-friendly and provides a step-by-step approach to calculating the section modulus. The calculator also provides a detailed report of the calculations, including the input parameters, intermediate calculations, and the final result.
Advantages of using the Universal Calculator
There are several advantages to using the Section Modulus S for I Beam Universal Calculator. The calculator provides accurate and efficient calculations, saving time and reducing the risk of errors. The calculator also provides a comprehensive report of the calculations, allowing users to understand the underlying assumptions and calculations. Additionally, the calculator is easy to use and requires minimal input from the user, making it a valuable tool for structural engineers and designers.
Common Applications of the Universal Calculator
The Section Modulus S for I Beam Universal Calculator has a wide range of applications in structural engineering and design. The calculator is commonly used to design and analyze steel structures, such as bridges, buildings, and industrial facilities. The calculator is also used to design and analyze concrete structures, such as slabs, beams, and columns. Additionally, the calculator is used to design and analyze composite structures, such as steel-concrete composite beams and columns.
Limitations and Assumptions of the Universal Calculator
While the Section Modulus S for I Beam Universal Calculator is a powerful tool, it is essential to understand its limitations and assumptions. The calculator assumes that the beam is a prismatic beam, with a constant cross-sectional area along its length. The calculator also assumes that the beam is subjected to static loading, and does not account for dynamic loading or impact loads. The calculator also has limitations in terms of the beam shapes and sizes that it can handle, and users should consult the user manual for specific limitations and assumptions.
| Parameter | Description |
|---|---|
| Section Modulus | The ratio of the moment of inertia of the beam's cross-section to the distance from the neutral axis to the extreme fiber |
| Cross-Sectional Area | The area of the beam's cross-section, typically measured in square inches or square millimeters |
| Distance from Neutral Axis | The distance from the neutral axis to the extreme fiber, typically measured in inches or millimeters |
| Moment of Inertia | A measure of the beam's resistance to bending, typically measured in inches to the fourth power or millimeters to the fourth power |
| Beam Shape and Size | The shape and size of the beam, including the width, depth, and thickness of the flanges and web |
How to calculate the section modulus of an I beam?
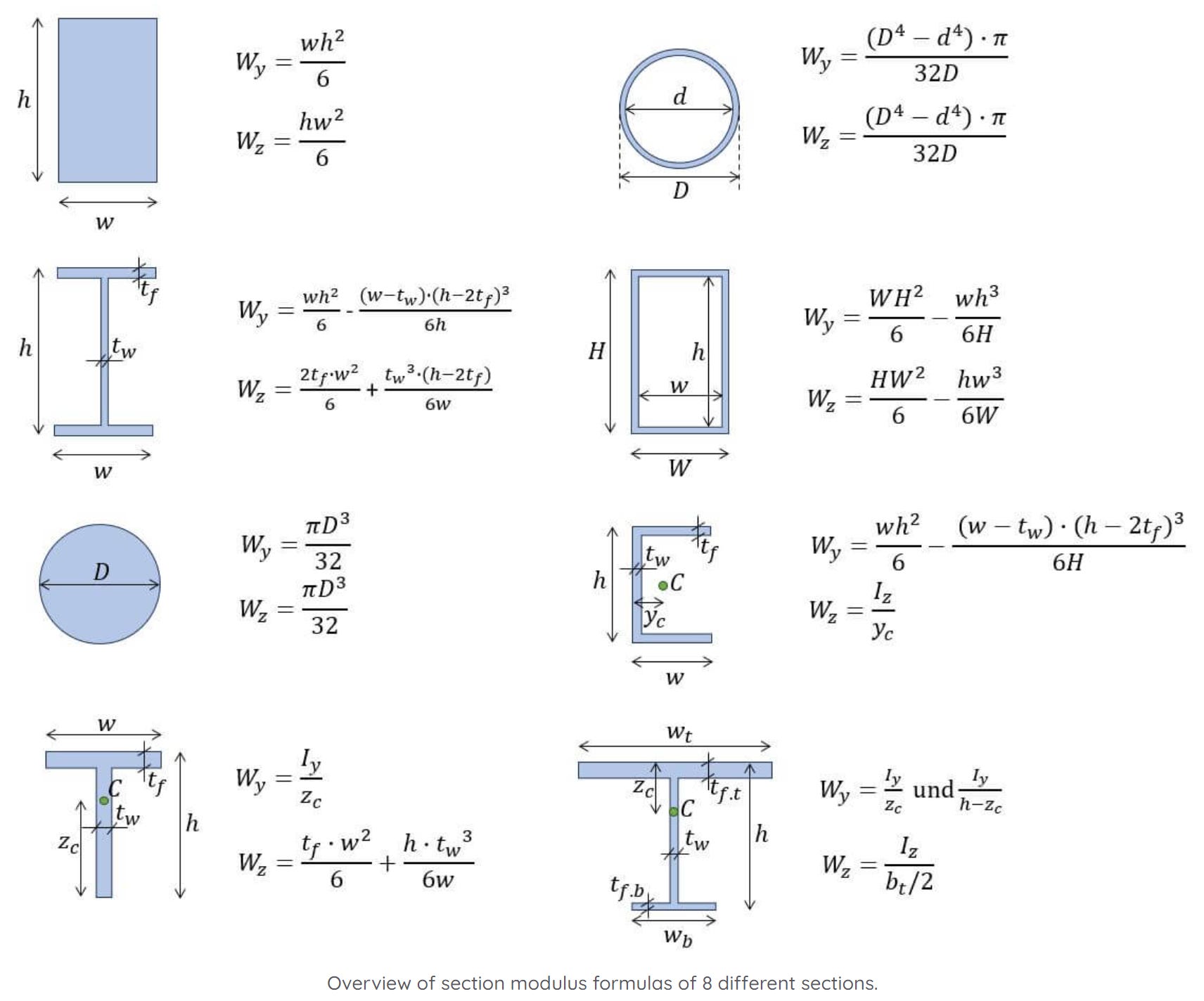
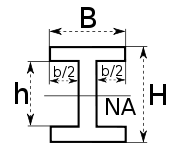
To calculate the section modulus of an I beam, you need to know the beam's dimensions, including its depth, width, and thickness of the flanges and web. The section modulus is a measure of the beam's ability to resist bending and is calculated using the formula: S = (I/c), where S is the section modulus, I is the moment of inertia, and c is the distance from the neutral axis to the extreme fiber of the beam.
Understanding the Dimensions of an I Beam
To calculate the section modulus, you first need to understand the dimensions of an I beam. The dimensions include the depth (d), width (b), thickness of the flanges (tf), and thickness of the web (tw). The depth is the overall height of the beam, while the width is the overall width of the beam. The flanges are the horizontal parts of the beam, and the web is the vertical part of the beam.
- The depth (d) is the overall height of the beam.
- The width (b) is the overall width of the beam.
- The flanges have a thickness (tf) that is typically smaller than the web thickness (tw).
Calculating the Moment of Inertia
The moment of inertia (I) is a measure of the beam's resistance to bending and is calculated using the formula: I = (bd^3)/12 - (tw(d-2tf)^3)/12, where bd^3/12 is the moment of inertia of the full beam and tw(d-2tf)^3/12 is the moment of inertia of the web.
- The moment of inertia (I) is calculated using the beam's dimensions.
- The formula for the moment of inertia takes into account the beam's depth, width, and thickness of the flanges and web.
- The result is a measure of the beam's resistance to bending.
Determining the Neutral Axis
The neutral axis is the line that runs through the center of the beam and is the axis around which the beam bends. The neutral axis is typically located at the center of the beam, but can be affected by the asymmetry of the beam's cross-section.
- The neutral axis is the line that runs through the center of the beam.
- The neutral axis is the axis around which the beam bends.
- The location of the neutral axis can be affected by the asymmetry of the beam's cross-section.
Calculating the Section Modulus
The section modulus (S) is calculated using the formula: S = (I/c), where I is the moment of inertia and c is the distance from the neutral axis to the extreme fiber of the beam. The section modulus is a measure of the beam's ability to resist bending and is used to calculate the stress and strain on the beam.
- The section modulus (S) is calculated using the moment of inertia and the distance to the extreme fiber.
- The result is a measure of the beam's ability to resist bending.
- The section modulus is used to calculate the stress and strain on the beam.
Applying the Section Modulus in Engineering
The section modulus is an important parameter in engineering and is used to design and analyze beams and other structural elements. By calculating the section modulus, engineers can determine the stress and strain on a beam and ensure that it can withstand the loads and forces that it will be subjected to.
- The section modulus is an important parameter in engineering.
- The section modulus is used to design and analyze beams and other structural elements.
- The result is used to ensure that the beam can withstand the loads and forces that it will be subjected to.
What is the elastic section modulus of the I section?

The elastic section modulus of an I-section is a measure of its ability to resist bending and is calculated as the ratio of the moment of inertia to the distance from the neutral axis to the extreme fiber. It is an important parameter in determining the section's ability to withstand bending stresses and is used in the design of structural elements such as beams and columns. The elastic section modulus is typically denoted by the symbol S and is calculated using the formula S = I/y, where I is the moment of inertia and y is the distance from the neutral axis to the extreme fiber.
Introduction to Elastic Section Modulus
The elastic section modulus is a fundamental concept in structural analysis and is used to determine the stress and strain in a beam or column under load. The elastic section modulus is a measure of the section's ability to resist bending and is calculated as the ratio of the moment of inertia to the distance from the neutral axis to the extreme fiber. The key factors that affect the elastic section modulus of an I-section include:
- The moment of inertia of the section, which is a measure of the section's ability to resist bending
- The distance from the neutral axis to the extreme fiber, which affects the stress and strain in the section
- The section's geometry, including the web and flange thicknesses and the overall height of the section
Calculating Elastic Section Modulus
To calculate the elastic section modulus of an I-section, the moment of inertia and the distance from the neutral axis to the extreme fiber must be determined. The moment of inertia can be calculated using the formula I = (bh^3)/12, where b is the width of the section and h is the height. The distance from the neutral axis to the extreme fiber can be calculated using the formula y = h/2, where h is the height of the section. The key steps in calculating the elastic section modulus include:
- Calculating the moment of inertia using the section's geometry
- Calculating the distance from the neutral axis to the extreme fiber using the section's geometry
- Calculating the elastic section modulus using the formula S = I/y
Importance of Elastic Section Modulus
The elastic section modulus is an important parameter in determining the section's ability to withstand bending stresses and is used in the design of structural elements such as beams and columns. A higher elastic section modulus indicates a greater ability to resist bending and is often preferred in structural design. The key benefits of a high elastic section modulus include:
- Increased resistance to bending and stress
- Improved structural stability and safety
- Reduced deflection and vibration under load
Factors Affecting Elastic Section Modulus
The elastic section modulus of an I-section is affected by several factors, including the section's geometry, the material properties, and the loading conditions. The key factors that affect the elastic section modulus include:
- The section's geometry, including the web and flange thicknesses and the overall height of the section
- The material properties, including the elastic modulus and the yield strength
- The loading conditions, including the type and magnitude of the load
Applications of Elastic Section Modulus
The elastic section modulus has a wide range of applications in structural engineering, including the design of beams, columns, and other structural elements. The key applications of the elastic section modulus include:
- Design of beams and columns to withstand bending stresses and loads
- Calculation of stress and strain in structural elements under load
- Determination of the structural stability and safety of buildings and other structures
What is the formula for section modulus z?
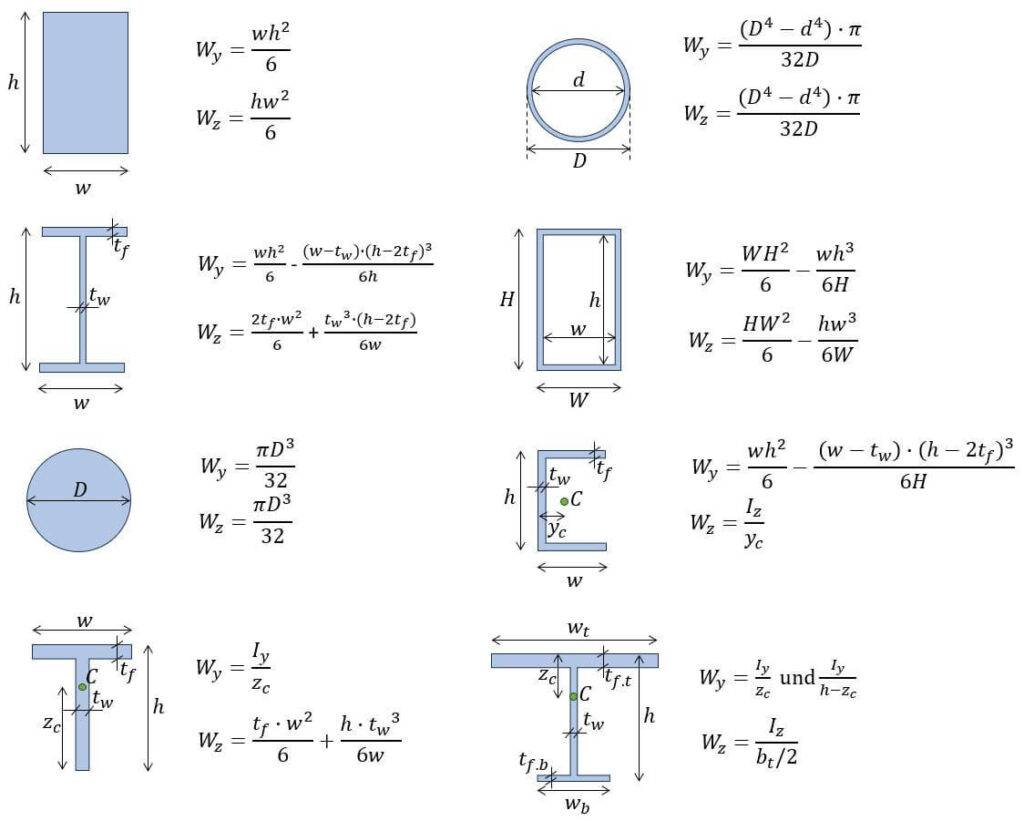
The formula for section modulus z is given by z = I / y, where I is the moment of inertia of the cross-sectional area and y is the distance from the neutral axis to the extreme fiber of the section. This formula is used to calculate the flexural rigidity of a beam and is an important parameter in structural engineering.
Introduction to Section Modulus
The section modulus z is a measure of the flexural rigidity of a beam, which is the ability of the beam to resist bending. It is an important parameter in structural engineering and is used to calculate the stress and strain on a beam under load. The formula for section modulus z is used to calculate the flexural rigidity of a beam, which is given by the product of the moment of inertia I and the modulus of elasticity E.
- The section modulus z is calculated using the formula z = I / y.
- The moment of inertia I is calculated using the formula I = ∫y^2 dA, where y is the distance from the neutral axis to the extreme fiber of the section and dA is the infinitesimal area element.
- The neutral axis is the axis about which the beam bends, and it is the axis that passes through the centroid of the cross-sectional area.
Calculating Moment of Inertia
The moment of inertia I is a measure of the resistance of a beam to bending and is calculated using the formula I = ∫y^2 dA. This formula is used to calculate the moment of inertia of a beam with a complex cross-sectional area. The moment of inertia I is an important parameter in structural engineering and is used to calculate the section modulus z and the flexural rigidity of a beam.
- The moment of inertia I is calculated using the formula I = ∫y^2 dA.
- The infinitesimal area element dA is used to calculate the moment of inertia of a beam with a complex cross-sectional area.
- The centroid of the cross-sectional area is used to calculate the neutral axis of the beam.
Understanding Flexural Rigidity
The flexural rigidity of a beam is a measure of its ability to resist bending and is calculated using the formula EI, where E is the modulus of elasticity and I is the moment of inertia. The flexural rigidity of a beam is an important parameter in structural engineering and is used to calculate the stress and strain on a beam under load. The section modulus z is used to calculate the flexural rigidity of a beam.
- The flexural rigidity of a beam is calculated using the formula EI.
- The modulus of elasticity E is a measure of the stiffness of a material.
- The section modulus z is used to calculate the flexural rigidity of a beam.
Importance of Section Modulus in Structural Engineering
The section modulus z is an important parameter in structural engineering and is used to calculate the stress and strain on a beam under load. The section modulus z is used to design structurally sound beams that can resist bending and twisting. The section modulus z is also used to calculate the deflection of a beam under load.
- The section modulus z is used to calculate the stress and strain on a beam under load.
- The section modulus z is used to design structurally sound beams.
- The section modulus z is used to calculate the deflection of a beam under load.
Applications of Section Modulus in Real-World Scenarios
The section modulus z has numerous real-world applications in structural engineering, including the design of bridges, buildings, and aircraft. The section modulus z is used to calculate the stress and strain on a beam under load and to design structurally sound beams that can resist bending and twisting. The section modulus z is also used to calculate the deflection of a beam under load.
- The section modulus z is used to design bridges and buildings.
- The section modulus z is used to calculate the stress and strain on a beam under load.
- The section modulus z is used to calculate the deflection of a beam under load.
Frequently Asked Questions (FAQs)
What is the Section Modulus S for I Beam Universal Calculator and how does it work?
The Section Modulus S for I Beam Universal Calculator is a mathematical tool used to calculate the section modulus of an I-beam, which is a critical parameter in determining the beam's ability to resist bending and torsion. This calculator is designed to provide a quick and accurate way to calculate the section modulus of an I-beam, taking into account the beam's dimensions, material properties, and loading conditions. The calculator uses the formula for section modulus, which is based on the beam's moment of inertia and distance from the neutral axis. By inputting the relevant parameters, the calculator can provide the section modulus value, which can be used to determine the beam's strength and stiffness.
What are the key parameters required to calculate the Section Modulus S for an I Beam?
To calculate the Section Modulus S for an I-beam, several key parameters are required, including the beam's width, height, flange thickness, web thickness, and material density. The width and height of the beam are used to calculate the moment of inertia, while the flange thickness and web thickness are used to calculate the section modulus. The material density is used to calculate the weight of the beam, which is important in determining the loading conditions. Additionally, the loading conditions, such as the applied load and support conditions, are also required to calculate the section modulus. The calculator can handle various types of loading conditions, including point loads, uniformly distributed loads, and moment loads.
How does the Section Modulus S for I Beam Universal Calculator handle different types of loading conditions?
The Section Modulus S for I Beam Universal Calculator is designed to handle various types of loading conditions, including point loads, uniformly distributed loads, and moment loads. The calculator uses the principle of superposition to combine the effects of multiple loads, allowing it to handle complex loading conditions. For point loads, the calculator uses the formula for the section modulus at a point, which takes into account the distance from the neutral axis and the moment of inertia. For uniformly distributed loads, the calculator uses the formula for the section modulus over a length, which takes into account the length of the beam and the loading intensity. The calculator can also handle moment loads, which are used to calculate the section modulus due to torsion.
What are the benefits of using the Section Modulus S for I Beam Universal Calculator in engineering design and analysis?
The Section Modulus S for I Beam Universal Calculator offers several benefits in engineering design and analysis, including increased accuracy, reduced calculation time, and improved design optimization. The calculator can help engineers and designers to quickly and accurately calculate the section modulus of an I-beam, which is critical in determining the beam's strength and stiffness. The calculator can also help to optimize the design of the beam, by allowing users to iterate on different design parameters and loading conditions. Additionally, the calculator can be used to verify the results of finite element analysis and other numerical methods, providing a quick and reliable way to check the validity of the results. The calculator is also user-friendly, with a simple and intuitive interface that makes it easy to use, even for users with limited experience in structural analysis.
Deja una respuesta

Entradas Relacionadas