Rectangular Plate Mass Moment of Inertia Calculator on Edge

The Rectangular Plate Mass Moment of Inertia Calculator on Edge is a valuable tool for engineers and physicists to calculate the moment of inertia of a rectangular plate. This calculation is crucial in determining the plate's resistance to changes in its rotational motion. The moment of inertia depends on the plate's mass, dimensions, and axis of rotation. By using this calculator, users can easily determine the moment of inertia of a rectangular plate rotating around its edge, making it an essential resource for designing and analyzing various mechanical systems and structures. Its accuracy is highly reliable.
https://youtube.com/watch?v=oeC_D3rb4kM
- Calculating the Mass Moment of Inertia of a Rectangular Plate on Edge
- What is the formula for the mass moment of inertia of a rectangle?
- What is the moment of inertia of a thin plate?
- What is the mass moment of inertia of a square plate?
-
Frequently Asked Questions (FAQs)
- What is the Rectangular Plate Mass Moment of Inertia Calculator on Edge and how does it work?
- What are the key factors that affect the mass moment of inertia of a rectangular plate on edge?
- How is the mass moment of inertia of a rectangular plate on edge used in real-world applications?
- What are the limitations and assumptions of the Rectangular Plate Mass Moment of Inertia Calculator on Edge?
Calculating the Mass Moment of Inertia of a Rectangular Plate on Edge
The mass moment of inertia is a fundamental concept in mechanics and engineering, particularly in the study of rotational motion. When a rectangular plate is placed on its edge, its mass moment of inertia changes due to the altered orientation of its mass distribution. To calculate this, we can use the formula for mass moment of inertia, which takes into account the plate's dimensions, mass, and axis of rotation.
Understanding the Concept of Mass Moment of Inertia
The mass moment of inertia is a measure of an object's resistance to changes in its rotational motion. It depends on the object's mass distribution and the axis of rotation. For a rectangular plate, the mass moment of inertia about its edge can be calculated using the parallel axis theorem. This theorem states that the mass moment of inertia about a new axis is equal to the mass moment of inertia about the original axis plus the product of the mass and the distance between the two axes squared.
Derivation of the Formula for Mass Moment of Inertia
The formula for the mass moment of inertia of a rectangular plate about its edge can be derived by integrating the elemental areas of the plate and their distances from the axis of rotation. The resulting formula is given by: I = (1/12) m (a^2 + b^2), where I is the mass moment of inertia, m is the mass of the plate, a is the length of the plate, and b is the width of the plate.
Importance of Mass Moment of Inertia in Engineering Applications
The mass moment of inertia is crucial in various engineering applications, such as mechanical engineering, aerospace engineering, and civil engineering. It is used to calculate the torque and angular acceleration of rotating objects, which is essential in the design of machines, vehicles, and structures. Additionally, the mass moment of inertia is used to determine the stability and balance of rotating systems.
Rectangular Plate Mass Moment of Inertia Calculator on Edge
A rectangular plate mass moment of inertia calculator on edge is a tool used to calculate the mass moment of inertia of a rectangular plate when it is placed on its edge. This calculator can be used by engineers and designers to quickly and accurately calculate the mass moment of inertia of a rectangular plate, which is essential in the design and analysis of rotating systems. The calculator takes into account the plate's dimensions, mass, and axis of rotation to provide an accurate calculation of the mass moment of inertia.
Applications of Rectangular Plate Mass Moment of Inertia Calculator
The rectangular plate mass moment of inertia calculator on edge has various applications in engineering and design. It can be used to calculate the mass moment of inertia of gears, pulleys, and flywheels, which are common components in mechanical systems. Additionally, the calculator can be used to determine the stability and balance of rotating systems, such as helicopters and wind turbines.
| Parameter | Unit | Description |
|---|---|---|
| m | kg | Mass of the rectangular plate |
| a | m | Length of the rectangular plate |
| b | m | Width of the rectangular plate |
| I | kgm^2 | Mass moment of inertia of the rectangular plate about its edge |
What is the formula for the mass moment of inertia of a rectangle?

The formula for the mass moment of inertia of a rectangle is given by I = (1/12) m (a^2 + b^2), where I is the mass moment of inertia, m is the mass of the rectangle, and a and b are the length and width of the rectangle, respectively.
Introduction to Moment of Inertia
The moment of inertia is a measure of an object's resistance to changes in its rotation. It depends on the mass distribution of the object and the axis of rotation. For a rectangle, the moment of inertia can be calculated using the formula I = (1/12) m (a^2 + b^2). This formula is derived from the integral of the mass elements of the rectangle with respect to the axis of rotation.
- The mass moment of inertia is an important concept in physics and engineering.
- It is used to calculate the torque and angular acceleration of an object.
- The moment of inertia is a tensor quantity, which means it has both magnitude and direction.
Derivation of the Formula
The formula for the mass moment of inertia of a rectangle can be derived by integrating the mass elements of the rectangle with respect to the axis of rotation. This involves using the integral calculus to sum up the moments of inertia of the infinitesimal mass elements. The resulting formula is I = (1/12) m (a^2 + b^2), where m is the mass of the rectangle, and a and b are the length and width of the rectangle, respectively.
- The derivation of the formula involves using the integral calculus.
- The mass elements of the rectangle are integrated with respect to the axis of rotation.
- The resulting formula is a simple expression that can be easily evaluated.
Applications of the Formula
The formula for the mass moment of inertia of a rectangle has many practical applications in physics and engineering. It is used to calculate the torque and angular acceleration of an object, and to design popular machines such as cars and airplanes. The formula is also used in sports to calculate the momentum and kinetic energy of an athlete.
- The formula has many practical applications in physics and engineering.
- It is used to calculate the torque and angular acceleration of an object.
- The formula is also used in sports to calculate the momentum and kinetic energy of an athlete.
Moment of Inertia of a Rectangle about Its Center
The moment of inertia of a rectangle about its center can be calculated using the formula I = (1/12) m (a^2 + b^2), where m is the mass of the rectangle, and a and b are the length and width of the rectangle, respectively. This formula is symmetric about the center of the rectangle, which means that the moment of inertia is the same about any axis that passes through the center.
- The moment of inertia of a rectangle about its center is a fundamental concept.
- The formula is symmetric about the center of the rectangle.
- The moment of inertia is the same about any axis that passes through the center.
Comparison with Other Shapes
The moment of inertia of a rectangle can be compared with that of other shapes, such as a circle or a triangle. The formula for the moment of inertia of a rectangle is simple and easy to evaluate, whereas the formulas for other shapes can be more complicated. The moment of inertia of a rectangle is also dependent on the mass distribution of the object, which can affect its rotational dynamics.
- The moment of inertia of a rectangle can be compared with that of other shapes.
- The formula for the moment of inertia of a rectangle is simple and easy to evaluate.
- The moment of inertia is dependent on the mass distribution of the object.
What is the moment of inertia of a thin plate?
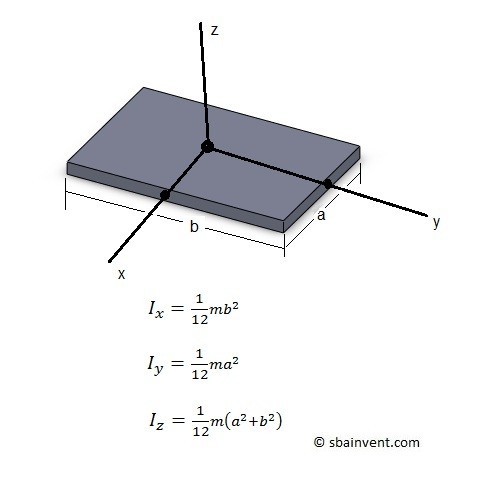
The moment of inertia of a thin plate is a measure of its resistance to changes in its rotational motion. It depends on the mass distribution of the plate and the axis of rotation. For a thin plate, the moment of inertia can be calculated using the following formulas: I = (1/12) m (a^2 + b^2) for rotation around an axis perpendicular to the plate, and I = (1/3) m (a^2) for rotation around an axis parallel to the plate, where m is the mass of the plate, and a and b are the dimensions of the plate.
Understanding the Moment of Inertia of a Thin Plate
The moment of inertia of a thin plate is an important concept in physics and engineering, as it helps to understand the rotational dynamics of objects. To calculate the moment of inertia, we need to consider the mass distribution of the plate and the axis of rotation. The following are some key points to consider:
- The moment of inertia depends on the mass of the plate and the dimensions of the plate.
- The axis of rotation is also an important factor, as it affects the moment of inertia.
- The moment of inertia can be calculated using the formulas I = (1/12) m (a^2 + b^2) and I = (1/3) m (a^2).
Calculating the Moment of Inertia of a Thin Plate
To calculate the moment of inertia of a thin plate, we need to use the following formulas: I = (1/12) m (a^2 + b^2) for rotation around an axis perpendicular to the plate, and I = (1/3) m (a^2) for rotation around an axis parallel to the plate. We can also use the parallel axis theorem to calculate the moment of inertia about a different axis. The following are some key steps:
- Identify the mass of the plate and the dimensions of the plate.
- Choose the axis of rotation and the reference point.
- Use the formulas I = (1/12) m (a^2 + b^2) and I = (1/3) m (a^2) to calculate the moment of inertia.
Factors Affecting the Moment of Inertia of a Thin Plate
The moment of inertia of a thin plate is affected by several factors, including the mass distribution of the plate and the axis of rotation. The following are some key factors:
- The mass of the plate affects the moment of inertia, as a heavier plate will have a larger moment of inertia.
- The dimensions of the plate also affect the moment of inertia, as a larger plate will have a larger moment of inertia.
- The axis of rotation is also an important factor, as it affects the moment of inertia.
Applications of the Moment of Inertia of a Thin Plate
The moment of inertia of a thin plate has several applications in physics and engineering, including the design of rotating systems and the analysis of vibrations. The following are some key applications:
- The moment of inertia is used to design rotating systems, such as gyroscopes and flywheels.
- The moment of inertia is used to analyze vibrations in mechanical systems.
- The moment of inertia is used to calculate the torque and angular acceleration of a rotating system.
Rotational Kinematics and the Moment of Inertia of a Thin Plate
The rotational kinematics of a thin plate is closely related to its moment of inertia. The following are some key concepts:
- The angular velocity and angular acceleration of a rotating system are related to the moment of inertia.
- The torque and rotational kinetic energy of a rotating system are also related to the moment of inertia.
- The moment of inertia is an important concept in understanding the rotational dynamics of objects.
What is the mass moment of inertia of a square plate?

The mass moment of inertia of a square plate is a physical property that describes the resistance of the plate to changes in its rotational motion. It is a measure of the inertia of the plate around a particular axis, and it depends on the mass and geometry of the plate.
Introduction to Mass Moment of Inertia
The mass moment of inertia is an important concept in physics and engineering, as it is used to calculate the torque and angular acceleration of an object. For a square plate, the mass moment of inertia can be calculated using the formula: I = (1/12) m (a^2 + b^2), where m is the mass of the plate, and a and b are the lengths of the sides of the plate.
- The mass of the plate is a critical factor in determining the mass moment of inertia.
- The geometry of the plate, including the lengths and widths of the sides, also plays a significant role.
- The axis of rotation is also an important consideration, as the mass moment of inertia can vary depending on the axis around which the plate is rotating.
Calculating Mass Moment of Inertia for a Square Plate
To calculate the mass moment of inertia for a square plate, we need to know the mass and dimensions of the plate. We can use the formula I = (1/12) m (a^2 + b^2), where m is the mass of the plate, and a and b are the lengths of the sides of the plate.
- We need to measure the mass of the plate using a balance or other measurement device.
- We need to measure the lengths and widths of the sides of the plate using a ruler or other measurement device.
- We can then plug these values into the formula to calculate the mass moment of inertia.
Factors Affecting Mass Moment of Inertia
There are several factors that can affect the mass moment of inertia of a square plate, including the mass and geometry of the plate, as well as the axis of rotation.
- The mass of the plate is a critical factor, as a more massive plate will have a higher mass moment of inertia.
- The geometry of the plate, including the lengths and widths of the sides, also plays a significant role, as a plate with a larger moment arm will have a higher mass moment of inertia.
- The axis of rotation is also an important consideration, as the mass moment of inertia can vary depending on the axis around which the plate is rotating.
Applications of Mass Moment of Inertia
The mass moment of inertia has many practical applications in fields such as engineering and physics.
- It is used to calculate the torque and angular acceleration of an object, which is critical in the design of machines and mechanisms.
- It is used to determine the stability of an object, which is important in the design of buildings and bridges.
- It is used to calculate the energy required to rotate an object, which is critical in the design of motors and generators.
Importance of Mass Moment of Inertia in Real-World Scenarios
The mass moment of inertia is a critical concept in many real-world scenarios, including the design of machines, mechanisms, and structures.
- In the design of cars, the mass moment of inertia is used to calculate the torque and angular acceleration of the wheels.
- In the design of airplanes, the mass moment of inertia is used to calculate the torque and angular acceleration of the propellers.
- In the design of buildings, the mass moment of inertia is used to determine the stability of the structure.
Frequently Asked Questions (FAQs)
What is the Rectangular Plate Mass Moment of Inertia Calculator on Edge and how does it work?
The Rectangular Plate Mass Moment of Inertia Calculator on Edge is a tool designed to calculate the mass moment of inertia of a rectangular plate when it is rotated around its edge. This calculator is particularly useful in engineering and physics applications, where understanding the inertial properties of objects is crucial. The calculator takes into account the density, length, width, and thickness of the plate to determine its mass moment of inertia. By using this calculator, users can quickly and accurately determine the inertial properties of a rectangular plate, which is essential for designing and analyzing mechanical systems.
What are the key factors that affect the mass moment of inertia of a rectangular plate on edge?
The mass moment of inertia of a rectangular plate on edge is affected by several key factors, including the density of the material, the length and width of the plate, and its thickness. The density of the material is a critical factor, as it determines the mass of the plate, which in turn affects its inertial properties. The length and width of the plate also play a significant role, as they determine the distribution of mass around the axis of rotation. Additionally, the thickness of the plate can also impact its mass moment of inertia, particularly if it is rotated around its edge. By understanding how these factors interact, users can use the Rectangular Plate Mass Moment of Inertia Calculator on Edge to make informed decisions about their designs.
How is the mass moment of inertia of a rectangular plate on edge used in real-world applications?
The mass moment of inertia of a rectangular plate on edge has numerous real-world applications in engineering and physics. For example, in mechanical engineering, understanding the inertial properties of a rectangular plate is essential for designing rotating systems, such as gears, pulleys, and flywheels. In aerospace engineering, the mass moment of inertia of a rectangular plate is used to analyze the stability and control of aircraft and spacecraft. Additionally, in civil engineering, the mass moment of inertia of a rectangular plate is used to design bridges and buildings that can withstand seismic loads and other dynamic forces. By using the Rectangular Plate Mass Moment of Inertia Calculator on Edge, users can quickly and accurately determine the inertial properties of a rectangular plate, which is essential for a wide range of real-world applications.
What are the limitations and assumptions of the Rectangular Plate Mass Moment of Inertia Calculator on Edge?
The Rectangular Plate Mass Moment of Inertia Calculator on Edge is a useful tool for calculating the mass moment of inertia of a rectangular plate, but it does have some limitations and assumptions. For example, the calculator assumes that the plate is homogeneous and isotropic, meaning that its density and material properties are uniform throughout. Additionally, the calculator assumes that the plate is rigid, meaning that it does not deform or change shape when rotated. The calculator also assumes that the axis of rotation is perpendicular to the plate and passes through its edge. By understanding these limitations and assumptions, users can use the Rectangular Plate Mass Moment of Inertia Calculator on Edge with confidence, but also be aware of its potential restrictions and sources of error.
Deja una respuesta

Entradas Relacionadas