Flow Velocity in Straight Sewers Formula and Calculator

The flow velocity in straight sewers is a crucial parameter in wastewater management and engineering. It determines the efficiency of sewer systems, helping to prevent clogs, flooding, and environmental hazards. Calculating flow velocity accurately is essential for designing and maintaining effective sewer networks. The formula for flow velocity in straight sewers takes into account the flow rate, cross-sectional area, and other factors. A calculator can simplify this process, providing quick and reliable results for engineers and professionals working on sewer system design and optimization projects, ensuring that sewer systems operate efficiently and safely. This facilitates optimal system performance.
- Flow Velocity in Straight Sewers Formula and Calculator
- How do you calculate flow velocity?
- What is the formula for the velocity of flow in a pipe?
- What is the rule of thumb for pipe flow velocity?
- What is the velocity in sewers?
-
Frequently Asked Questions (FAQs)
- What is the formula for calculating flow velocity in straight sewers?
- How does the flow velocity in straight sewers affect the design of sewer systems?
- What are the advantages of using a calculator for flow velocity in straight sewers?
- What are the limitations of the flow velocity in straight sewers formula and calculator?
Flow Velocity in Straight Sewers Formula and Calculator
The flow velocity in straight sewers is a critical parameter in the design and operation of sewer systems. It is defined as the average velocity of the fluid (wastewater or stormwater) flowing through the sewer pipe. The flow velocity is often calculated using the Manning's Equation, which takes into account the pipe's diameter, slope, and roughness. The formula for calculating flow velocity in straight sewers is: V = (1/n) R^2/3 S^1/2, where V is the flow velocity, n is the Manning's roughness coefficient, R is the hydraulic radius, and S is the slope of the pipe.
Introduction to Flow Velocity in Straight Sewers
The flow velocity in straight sewers is an important factor in determining the hydraulic gradient and the flow rate of the sewer system. A higher flow velocity can lead to increased turbulence and scouring of the pipe, while a lower flow velocity can result in sedimentation and clogging of the pipe. The flow velocity in straight sewers can be affected by various factors, including the pipe's material, diameter, and slope, as well as the fluid properties and inflow rates.
Formula for Calculating Flow Velocity in Straight Sewers
The formula for calculating flow velocity in straight sewers is based on the Manning's Equation, which is: V = (1/n) R^2/3 S^1/2. This equation can be used to calculate the flow velocity in a straight sewer pipe, given the pipe's diameter, slope, and roughness. The Manning's roughness coefficient (n) is a measure of the pipe's roughness and can be determined using various methods, including the Hazen-Williams Equation.
Factors Affecting Flow Velocity in Straight Sewers
Several factors can affect the flow velocity in straight sewers, including:
| Factor | Description |
|---|---|
| Pipe Material | The type of material used for the pipe can affect its roughness and hydraulic properties. |
| Pipe Diameter | The diameter of the pipe can affect the flow rate and flow velocity of the sewer system. |
| Pipe Slope | The slope of the pipe can affect the flow velocity and hydraulic gradient of the sewer system. |
| Fluid Properties | The density and viscosity of the fluid can affect the flow velocity and flow rate of the sewer system. |
| Inflow Rates | The inflow rates of wastewater or stormwater can affect the flow velocity and flow rate of the sewer system. |
These factors can be taken into account when designing and operating sewer systems to ensure that the flow velocity is within the optimal range for the system.
Importance of Flow Velocity in Straight Sewers
The flow velocity in straight sewers is crucial for maintaining the hydraulic stability and efficiency of the sewer system. A high flow velocity can help to prevent sedimentation and clogging of the pipe, while a low flow velocity can lead to sedimentation and clogging of the pipe. The flow velocity can also affect the turbulence and scouring of the pipe, which can lead to erosion and damage to the pipe.
Calculator for Flow Velocity in Straight Sewers
A calculator for flow velocity in straight sewers can be used to calculate the flow velocity in a straight sewer pipe, given the pipe's diameter, slope, and roughness. The calculator can use the Manning's Equation to calculate the flow velocity and can take into account various factors, including the pipe's material, diameter, and slope, as well as the fluid properties and inflow rates. The calculator can be a useful tool for designing and operating sewer systems, allowing engineers to optimize the flow velocity and ensure that the system is operating efficiently and effectively. The calculator can also be used to predict the flow velocity in different scenarios, such as storm events or wastewater overflows, and can help engineers to design and operate the sewer system to mitigate these events. The use of strong and accurate calculators can help to ensure that the flow velocity in straight sewers is optimal and that the sewer system is operating safely and efficiently.
How do you calculate flow velocity?
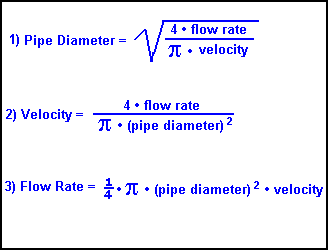
To calculate flow velocity, you need to understand the concept of fluid dynamics and the factors that affect the movement of fluids. Flow velocity is the speed at which a fluid flows through a given area, and it is typically measured in meters per second (m/s) or feet per second (ft/s). The calculation of flow velocity involves several parameters, including the cross-sectional area of the flow, the volume flow rate, and the density of the fluid.
Understanding the Concept of Flow Velocity
The concept of flow velocity is crucial in various fields, including engineering, physics, and chemistry. To calculate flow velocity, you need to understand the relationship between the volume flow rate and the cross-sectional area of the flow. The volume flow rate is the amount of fluid that flows through a given area per unit time, and it is typically measured in cubic meters per second (m³/s) or cubic feet per second (ft³/s). The cross-sectional area is the area through which the fluid flows, and it is typically measured in square meters (m²) or square feet (ft²). Some key factors to consider when calculating flow velocity include:
- Density of the fluid, which affects the flow velocity due to the varying viscosity and pressure
- Volume flow rate, which is the amount of fluid that flows through a given area per unit time
- Cross-sectional area, which is the area through which the fluid flows, affecting the flow velocity and pressure drop
Calculating Flow Velocity Using the Continuity Equation
The continuity equation is a fundamental concept in fluid dynamics that relates the flow velocity to the volume flow rate and the cross-sectional area. The equation states that the volume flow rate is equal to the product of the flow velocity and the cross-sectional area. To calculate flow velocity using the continuity equation, you need to know the volume flow rate and the cross-sectional area. Some key steps to follow include:
- Measure the volume flow rate using a flow meter or by calculating it from the mass flow rate and the density of the fluid
- Measure the cross-sectional area using a caliper or by calculating it from the diameter and the shape of the flow channel
- Apply the continuity equation to calculate the flow velocity, taking into account the units and the significance of the results
Factors Affecting Flow Velocity
Several factors can affect the flow velocity, including the viscosity of the fluid, the pressure drop, and the roughness of the flow channel. The viscosity of the fluid affects the flow velocity due to the frictional resistance to flow, while the pressure drop affects the flow velocity due to the energy loss. The roughness of the flow channel also affects the flow velocity due to the turbulence and energy dissipation. Some key factors to consider include:
- Viscosity, which affects the flow velocity due to the frictional resistance to flow, with higher viscosity resulting in lower flow velocity
- Pressure drop, which affects the flow velocity due to the energy loss, with higher pressure drop resulting in higher flow velocity
- Roughness, which affects the flow velocity due to the turbulence and energy dissipation, with higher roughness resulting in lower flow velocity
Measuring Flow Velocity
Measuring flow velocity is crucial in various applications, including engineering, physics, and chemistry. Several methods can be used to measure flow velocity, including the use of pilot tubes, hot wire anemometers, and laser Doppler velocimetry. The choice of method depends on the accuracy required, the flow conditions, and the equipment available. Some key considerations include:
- Accuracy, which depends on the method used, the calibration of the equipment, and the flow conditions
- Flow conditions, which affect the flow velocity measurement, including the turbulence, pressure drop, and viscosity
- Equipment, which includes the sensors, data acquisition systems, and software used to measure and analyze the flow velocity
Applications of Flow Velocity Calculation
Calculating flow velocity has several applications in various fields, including engineering, physics, and chemistry. Some key applications include:
- Pipe flow, where flow velocity is crucial in designing and optimizing pipeline systems, including the pump selection and pipeline sizing
- Fluid machinery, where flow velocity is important in designing and optimizing turbines, pumps, and compressors
- Chemical engineering, where flow velocity is crucial in designing and optimizing chemical reactors, mixers, and separators
What is the formula for the velocity of flow in a pipe?
The formula for the velocity of flow in a pipe is given by the Darcy-Weisbach equation, which is a widely used equation in fluid dynamics to calculate the velocity of fluid flow in a pipe. The equation is: V = (1/n) R^2/3 S^1/2, where V is the velocity of the fluid, n is the Manning's roughness coefficient, R is the hydraulic radius of the pipe, and S is the slope of the pipe.
Understanding the Darcy-Weisbach Equation
The Darcy-Weisbach equation is a fundamental equation in fluid dynamics that relates the velocity of fluid flow in a pipe to the friction factor, pipe diameter, and pressure drop. To understand this equation, it is essential to know the physical properties of the fluid, such as its density and viscosity, as well as the pipe characteristics, including its length, diameter, and roughness. The key points to consider are:
- The friction factor is a critical component of the Darcy-Weisbach equation, as it represents the resistance to flow caused by the pipe's roughness and viscosity of the fluid.
- The pipe diameter and length are also crucial factors, as they affect the velocity and pressure drop of the fluid flow.
- The physical properties of the fluid, such as its density and viscosity, play a significant role in determining the velocity of the fluid flow.
Factors Affecting Velocity of Flow
Several factors affect the velocity of flow in a pipe, including the pipe material, pipe size, fluid properties, and flow rate. The pipe material and size can significantly impact the friction factor, which in turn affects the velocity of the fluid flow. The fluid properties, such as its density and viscosity, also play a crucial role in determining the velocity of the fluid flow. The key points to consider are:
- The pipe material can affect the friction factor, with smooth pipes having a lower friction factor than rough pipes.
- The pipe size can impact the velocity of the fluid flow, with larger pipes typically having a higher velocity than smaller pipes.
- The fluid properties, such as its density and viscosity, can significantly affect the velocity of the fluid flow, with less viscous fluids having a higher velocity than more viscous fluids.
Calculating Velocity of Flow
To calculate the velocity of flow in a pipe, it is essential to know the flow rate, pipe diameter, and friction factor. The flow rate can be calculated using the continuity equation, which states that the mass flow rate is constant throughout the pipe. The pipe diameter and friction factor can be used to calculate the velocity of the fluid flow using the Darcy-Weisbach equation. The key points to consider are:
- The flow rate can be calculated using the continuity equation, which is given by: Q = A V, where Q is the flow rate, A is the cross-sectional area of the pipe, and V is the velocity of the fluid flow.
- The pipe diameter and friction factor can be used to calculate the velocity of the fluid flow using the Darcy-Weisbach equation.
- The physical properties of the fluid, such as its density and viscosity, must be known to calculate the velocity of the fluid flow.
Applications of Velocity of Flow
The velocity of flow in a pipe has numerous practical applications, including water supply systems, sewage systems, and industrial processes. Understanding the velocity of flow is crucial for designing and operating these systems efficiently and effectively. The key points to consider are:
- The velocity of flow is critical in water supply systems, as it affects the pressure and flow rate of the water.
- The velocity of flow is also important in sewage systems, as it affects the transportation of waste and the performance of the system.
- The velocity of flow is used in industrial processes, such as chemical processing and power generation, to optimize the efficiency and productivity of the process.
Importance of Accurate Velocity Measurements
Accurate velocity measurements are essential in various industrial applications, including fluid flow measurement, pipeline monitoring, and process control. Incorrect velocity measurements can lead to inaccurate calculations, inefficient operations, and reduced productivity. The key points to consider are:
- Accurate velocity measurements are crucial for fluid flow measurement, as they affect the calculation of flow rate and pressure drop.
- Velocity measurements are used in pipeline monitoring to detect leaks, blockages, and corrosion.
- Velocity measurements are also used in process control to optimize the efficiency and productivity of the process, and to ensure safe operation.
What is the rule of thumb for pipe flow velocity?
The rule of thumb for pipe flow velocity is a guideline that helps engineers and plumbers determine the maximum allowable velocity of fluid in a pipe to prevent erosion, vibration, and noise. The general rule of thumb is to keep the flow velocity below 5-7 feet per second (ft/s) for most applications, including water distribution systems, sewage systems, and industrial processes. However, this value can vary depending on the pipe material, fluid properties, and system requirements.
Introduction to Pipe Flow Velocity
The pipe flow velocity is a critical parameter in designing and operating pipe systems. A high flow velocity can cause turbulence, cavitation, and erosion, leading to pipe damage and system failure. On the other hand, a low flow velocity can result in sedimentation, corrosion, and microbial growth, which can also compromise the system integrity. To balance these factors, engineers use the rule of thumb for pipe flow velocity, which is based on experimental data and theoretical models. Some key factors to consider when determining the pipe flow velocity include:
- Pipe diameter and wall thickness
- Fluid density and viscosity
- System pressure and flow rate
Factors Affecting Pipe Flow Velocity
Several factors can affect the pipe flow velocity, including pipe roughness, bends, valves, and fittings. These factors can either increase or decrease the flow velocity, depending on the system configuration and operating conditions. For example, a smooth pipe can support higher flow velocities than a rough pipe, while a sharp bend can reduce the flow velocity due to turbulence and separation. Additionally, valves and fittings can introduce flow restrictions and pressure drops, which can also impact the pipe flow velocity. Some key factors to consider include:
- Pipe material and surface roughness
- Fittings and valves
- System layout and configuration
Pipe Flow Velocity Calculations
To calculate the pipe flow velocity, engineers use the continuity equation, which relates the flow rate to the pipe cross-sectional area and flow velocity. The continuity equation is given by Q = A v, where Q is the flow rate, A is the pipe cross-sectional area, and v is the flow velocity. Additionally, engineers can use the Darcy-Weisbach equation to calculate the head loss due to friction and turbulence. Some key equations to consider include:
- Continuity equation: Q = A v
- Darcy-Weisbach equation: h = f (L / D) (v^2 / 2g)
- Reynolds number: Re = ρ v D / μ
Applications of Pipe Flow Velocity
The pipe flow velocity has numerous applications in various fields, including water supply systems, sewage systems, industrial processes, and chemical processing. In these applications, the pipe flow velocity is critical in determining the system performance, efficiency, and reliability. For example, in water distribution systems, a high flow velocity can lead to water hammer and pipe damage, while a low flow velocity can result in stagnation and microbial growth. Some key applications to consider include:
- Water supply systems
- Sewage systems
- Industrial processes
Best Practices for Pipe Flow Velocity
To ensure optimal pipe flow velocity, engineers and plumbers should follow best practices, including proper pipe sizing, material selection, and system design. Additionally, regular maintenance and inspection are essential to prevent pipe damage and system failure. Some key best practices to consider include:
- Proper pipe sizing and material selection
- Regular maintenance and inspection
- System monitoring and control
What is the velocity in sewers?

The velocity in sewers is a critical factor in determining the efficiency and effectiveness of wastewater transport. It is essential to maintain a minimum velocity to prevent sedimentation and ensure that the wastewater flows smoothly through the sewer system. The velocity in sewers is influenced by various factors, including the slope of the sewer, the diameter of the pipe, and the flow rate of the wastewater.
Factors Affecting Velocity in Sewers
The velocity in sewers is affected by several factors, including the roughness of the pipe, the viscosity of the wastewater, and the friction losses in the system. These factors can be minimized by using smooth pipes, reducing bends and curves, and increasing the diameter of the pipe. Some key factors affecting velocity in sewers include:
- The slope of the sewer, which affects the gravity-driven flow of the wastewater
- The diameter of the pipe, which affects the flow rate and velocity of the wastewater
- The roughness of the pipe, which affects the friction losses and velocity of the wastewater
Design Considerations for Sewer Velocity
When designing sewer systems, it is essential to consider the velocity of the wastewater to ensure that the system operates efficiently and effectively. The design should take into account the peak flow rates, minimum velocity requirements, and pipe sizing to minimize sedimentation and blockages. Some key design considerations include:
- Sizing the pipe to accommodate the peak flow rates and minimum velocity requirements
- Sloping the sewer to ensure gravity-driven flow and minimize pumping requirements
- Using smooth pipes and reducing bends and curves to minimize friction losses
Measuring Velocity in Sewers
Measuring the velocity in sewers is crucial to ensure that the system is operating within the design parameters. Various methods can be used to measure velocity, including ultrasonic and magnetic flow meters. These methods provide accurate and reliable measurements of the velocity and flow rate of the wastewater. Some key methods for measuring velocity include:
- Ultrasonic flow meters, which use high-frequency sound waves to measure velocity and flow rate
- Magnetic flow meters, which use magnetic fields to measure velocity and flow rate
- Dye tracing, which uses tracers to measure velocity and flow rate
Velocity Requirements for Sewer Systems
The velocity requirements for sewer systems vary depending on the type of sewer and the wastewater characteristics. For example, stormwater sewers typically require a minimum velocity of 0.6 meters per second to prevent sedimentation and ensure that the system operates efficiently. Some key velocity requirements include:
- Minimum velocity of 0.6 meters per second for stormwater sewers
- Minimum velocity of 0.3 meters per second for sanitary sewers
- Maximum velocity of 3 meters per second to prevent erosion and damage to the pipe
Consequences of Low Velocity in Sewers
Low velocity in sewers can have serious consequences, including sedimentation, blockages, and overflows. Sedimentation can lead to reduced pipe capacity, increased maintenance costs, and environmental hazards. Some key consequences of low velocity include:
- Sedimentation, which can lead to reduced pipe capacity and increased maintenance costs
- Blockages, which can cause overflows and environmental hazards
- Increased energy costs, as pumping requirements increase to compensate for low velocity
Frequently Asked Questions (FAQs)
What is the formula for calculating flow velocity in straight sewers?
The formula for calculating flow velocity in straight sewers is based on the Manning equation, which is a widely used method for determining the velocity of fluid flow in open channels. The Manning equation is given by: V = (1/n) R^2/3 S^1/2, where V is the flow velocity, n is the Manning roughness coefficient, R is the hydraulic radius, and S is the slope of the sewer. The Manning roughness coefficient is a measure of the roughness of the sewer surface, and it can vary depending on the type of material used for the sewer and its condition. The hydraulic radius is the ratio of the cross-sectional area of the sewer to its wetted perimeter, and it is an important factor in determining the flow velocity. The slope of the sewer is also a critical factor, as it determines the head loss and the flow velocity.
How does the flow velocity in straight sewers affect the design of sewer systems?
The flow velocity in straight sewers plays a crucial role in the design of sewer systems, as it affects the capacity and efficiency of the system. A higher flow velocity can result in a greater capacity to transport wastewater, but it can also lead to increased erosion and wear on the sewer pipes. On the other hand, a lower flow velocity can result in a reduced capacity and increased sedimentation and clogging of the pipes. Therefore, it is essential to determine the optimal flow velocity for a given sewer system to ensure that it can transport wastewater efficiently and effectively. The design of the sewer system, including the size and slope of the pipes, must be carefully considered to achieve the optimal flow velocity. Additionally, the material used for the sewer pipes and the roughness of the surface can also impact the flow velocity and the overall performance of the system.
What are the advantages of using a calculator for flow velocity in straight sewers?
Using a calculator for flow velocity in straight sewers offers several advantages, including increased accuracy and efficiency. A calculator can quickly and easily perform complex calculations, reducing the likelihood of errors and saving time. Additionally, a calculator can be programmed to perform iterations and sensitivity analyses, allowing users to explore the impact of different design parameters on the flow velocity. This can be particularly useful for designing and optimizing sewer systems, as it allows users to evaluate different scenarios and identify the most effective solution. Furthermore, a calculator can also be used to perform real-time simulations, allowing users to monitor and adjust the flow velocity in response to changing conditions.
What are the limitations of the flow velocity in straight sewers formula and calculator?
The flow velocity in straight sewers formula and calculator have several limitations that must be considered when using them. One of the main limitations is that the formula assumes a steady-state flow condition, which may not always be the case in real-world sewer systems. Additionally, the formula does not account for turbulence and transient flows, which can significantly impact the flow velocity. Furthermore, the calculator is only as accurate as the input data, and errors in the input can result in inaccurate results. It is also important to note that the Manning equation is an empirical formula, and its accuracy can vary depending on the specific conditions of the sewer system. Therefore, it is essential to carefully evaluate the limitations of the formula and calculator and to consider additional factors, such as field measurements and experimental data, when designing and optimizing sewer systems.
Deja una respuesta

Entradas Relacionadas