Flat Plate Deflection Calculator
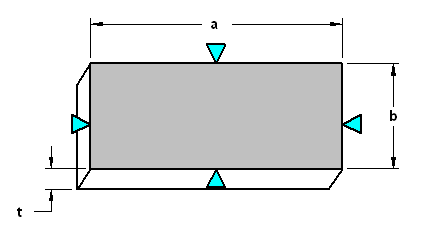
The Flat Plate Deflection Calculator is a valuable tool for engineers and designers to calculate the deflection of flat plates under various loads. It takes into account the material properties, plate dimensions, and boundary conditions to provide accurate results. This calculator is particularly useful in the design of structural components, such as bridges, buildings, and mechanical equipment. By using this calculator, users can quickly and easily determine the deflection of flat plates, ensuring the structural integrity and safety of their designs. It simplifies complex calculations and saves time in the design process.
- Understanding the Flat Plate Deflection Calculator
- What is the allowable deflection of a plate?
- What is the formula for calculating deflection?
- What is the deflection limit of a floor plate?
- How do you calculate deflection rate?
-
Frequently Asked Questions (FAQs)
- What is the Flat Plate Deflection Calculator and how does it work?
- What are the different types of loads that can be applied to the Flat Plate Deflection Calculator?
- What are the key factors that affect the deflection of a flat plate?
- How can the Flat Plate Deflection Calculator be used in real-world applications?
Understanding the Flat Plate Deflection Calculator
The Flat Plate Deflection Calculator is a tool used to calculate the deflection of a flat plate under various types of loading. The calculator takes into account the material properties, plate dimensions, and boundary conditions to determine the deflection and stress distributions within the plate. This calculator is essential in engineering and design applications where the structural integrity of flat plates is critical.
Introduction to Flat Plate Deflection
Flat plate deflection refers to the bending or deformation of a flat plate under external loads. The deflection can be caused by various types of loading, including uniformly distributed loads, point loads, and moment loads. The calculation of flat plate deflection is crucial in ensuring the safety and stability of structures, such as buildings, bridges, and aircraft.
Factors Affecting Flat Plate Deflection
Several factors affect the deflection of a flat plate, including the material properties, such as the modulus of elasticity and Poisson's ratio, the plate dimensions, such as the length, width, and thickness, and the boundary conditions, such as the support conditions and constraints. The calculator takes into account these factors to provide an accurate calculation of the deflection and stress distributions.
Types of Deflection Calculators
There are various types of deflection calculators available, including analytical and numerical methods. The analytical methods use mathematical equations to calculate the deflection, while the numerical methods use finite element analysis or finite difference methods. The Flat Plate Deflection Calculator uses a combination of analytical and numerical methods to provide a fast and accurate calculation of the deflection.
Applications of the Flat Plate Deflection Calculator
The Flat Plate Deflection Calculator has a wide range of applications in engineering and design, including structural analysis, mechanical design, and aerospace engineering. The calculator can be used to design and analyze flat plates, beams, and plates with holes. It can also be used to calculate the stress and strain distributions within the plate.
Benefits of Using the Flat Plate Deflection Calculator
The Flat Plate Deflection Calculator provides several benefits, including fast and accurate calculations, easy to use interface, and flexibility in terms of input parameters. The calculator can also be used to optimize the design of flat plates and reduce the weight and cost of the structure. The following table summarizes the benefits of using the Flat Plate Deflection Calculator:
| Benefits | Description |
|---|---|
| Fast Calculations | The calculator provides fast and accurate calculations of the deflection and stress distributions. |
| Easy to Use | The calculator has an easy to use interface that allows users to input parameters and obtain results quickly. |
| Flexibility | The calculator allows users to input various types of loading and boundary conditions, making it flexible and versatile. |
| Optimization | The calculator can be used to optimize the design of flat plates and reduce the weight and cost of the structure. |
| Cost Savings | The calculator can help reduce the cost of the structure by optimizing the design and reducing material waste. |
What is the allowable deflection of a plate?
The allowable deflection of a plate refers to the maximum amount of bending or deformation that a plate is permitted to undergo without exceeding its structural limits. This is an important consideration in the design and construction of various structures, such as buildings, bridges, and aircraft, where plates are used as primary components. The allowable deflection of a plate depends on several factors, including the material properties, plate thickness, and the applied loads.
Types of Deflection
The deflection of a plate can occur in different forms, including lateral and torsional deflections. Lateral deflection refers to the bending of the plate in a direction perpendicular to its surface, while torsional deflection refers to the twisting of the plate. The allowable deflection of a plate is typically specified in terms of the maximum allowable lateral deflection. Some of the key considerations for determining the allowable deflection of a plate include:
- Material properties, such as the modulus of elasticity and yield strength
- Plate thickness and geometry
- Applied loads, including point loads and distributed loads
Design Considerations
The design of a plate must take into account the allowable deflection to ensure that it can withstand the expected loads without excessive deformation. This requires careful consideration of the boundary conditions, such as the supports and constraints, as well as the loading conditions. The designer must also ensure that the plate is not subject to stress concentrations, which can lead to failure. Some of the key design considerations for plates include:
- Plate thickness and material selection
- Support conditions, including simply supported and clamped edges
- Load distribution, including uniform and non-uniform loads
Calculation Methods
The allowable deflection of a plate can be calculated using various analytical and numerical methods. The most common method is the small deflection theory, which assumes that the deflection is small compared to the plate thickness. For larger deflections, large deflection theory or finite element methods may be necessary. Some of the key calculation methods for determining the allowable deflection of a plate include:
- Classical plate theory, which assumes a linear stress-strain relationship
- Finite element method, which uses discretization to solve the governing equations
- Experimental methods, which use strain measurement and deflection measurement to determine the allowable deflection
Material Properties
The material properties of the plate play a crucial role in determining its allowable deflection. The most important properties are the modulus of elasticity, yield strength, and ultimate strength. The modulus of elasticity determines the stiffness of the plate, while the yield strength and ultimate strength determine its load-carrying capacity. Some of the key material properties that affect the allowable deflection of a plate include:
- Modulus of elasticity, which determines the stiffness of the plate
- Yield strength, which determines the load-carrying capacity of the plate
- Ultimate strength, which determines the maximum load that the plate can withstand
Failure Modes
The allowable deflection of a plate is closely related to its failure modes, which include yielding, buckling, and fracture. Yielding occurs when the stress in the plate exceeds the yield strength, while buckling occurs when the compressive stress exceeds the critical buckling stress. Fracture occurs when the stress in the plate exceeds the ultimate strength. Some of the key failure modes that can occur in a plate include:
- Yielding, which occurs when the stress exceeds the yield strength
- Buckling, which occurs when the compressive stress exceeds the critical buckling stress
- Fracture, which occurs when the stress exceeds the ultimate strength
What is the formula for calculating deflection?
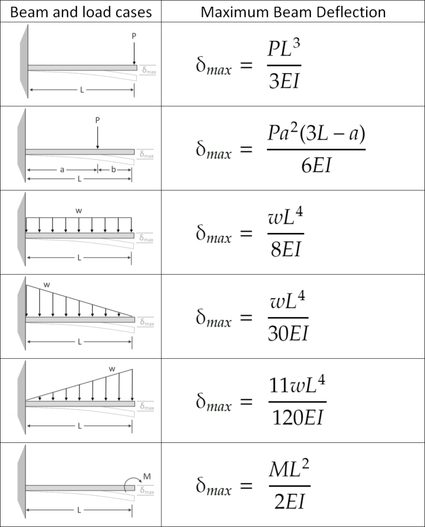
The formula for calculating deflection is a mathematical expression used to determine the amount of displacement or bending of a structural element, such as a beam, under a given load. The most common formula for calculating deflection is the beam deflection formula, which is given by the equation: Δ = (WL^3) / (3EI), where Δ is the deflection, W is the load, L is the length of the beam, E is the modulus of elasticity, and I is the moment of inertia.
Understanding the Variables
To calculate deflection, it is essential to understand the variables involved in the formula. The variables are:
- Load (W): The load applied to the beam, which can be a point load, a uniformly distributed load, or a varying load.
- Length (L): The length of the beam, which affects the stiffness and the ability of the beam to resist deflection.
- Modulus of Elasticity (E): The modulus of elasticity is a measure of the stiffness of the material, which determines how much the material will deform under a given load.
These variables are crucial in determining the deflection of a beam, and understanding their role is essential for accurate calculations.
Types of Deflection
There are several types of deflection that can occur in a beam, including:
- Vertical deflection: The vertical displacement of the beam under a load, which can be calculated using the beam deflection formula.
- Lateral deflection: The lateral displacement of the beam, which can occur due to a load applied in a direction perpendicular to the beam.
- Torsional deflection: The twisting of the beam, which can occur due to a torque applied to the beam.
Each type of deflection requires a different approach to calculation, and understanding the type of deflection is essential for accurate calculations.
Importance of Deflection Calculation
Calculating deflection is crucial in the design of structural elements, such as beams, columns, and trusses. The deflection calculation helps to determine the stability and safety of the structure, and ensures that it can withstand the applied loads.
- Structural integrity: The deflection calculation helps to ensure that the structure can withstand the applied loads without collapsing or failing.
- Safety: The deflection calculation helps to ensure that the structure is safe for use, and that it will not collapse or fail under normal operating conditions.
- Performance: The deflection calculation helps to ensure that the structure will perform as intended, and that it will not deform excessively under load.
Accurate deflection calculations are essential for ensuring the structural integrity, safety, and performance of a structure.
Factors Affecting Deflection
Several factors can affect the deflection of a beam, including:
- Material properties: The modulus of elasticity and poisson's ratio of the material can affect the deflection of the beam.
- Geometry: The shape and size of the beam can affect the deflection, with longer and thinner beams being more prone to deflection.
- Support conditions: The support conditions of the beam, such as simply supported or fixed, can affect the deflection.
Understanding these factors is essential for accurate deflection calculations, and for ensuring that the structure is designed to withstand the applied loads.
Calculating Deflection Using Software
In modern engineering practice, deflection calculations are often performed using computer-aided design (CAD) software and finite element analysis (FEA) tools. These tools allow engineers to model complex structures and calculate deflection under various loading conditions.
- CAD software: CAD software can be used to create a model of the structure, and to calculate deflection using built-in formulas and algorithms.
- FEA tools: FEA tools can be used to perform a detailed analysis of the structure, and to calculate deflection under various loading conditions.
- Validation: The results of the deflection calculation can be validated using experimental data and theoretical models.
Using software to calculate deflection can help to improve the accuracy and efficiency of the design process, and can help to ensure that the structure is safe and functional.
What is the deflection limit of a floor plate?
The deflection limit of a floor plate refers to the maximum allowable deflection or bending of the plate under load. This limit is crucial to ensure the structural integrity and safety of the floor. Exceeding the deflection limit can lead to collapse or damage to the floor and adjacent structures.
Design Considerations for Floor Plates
Design considerations for floor plates involve calculating the load-carrying capacity and deflection under various loads, including dead loads, live loads, and impact loads. To determine the deflection limit, engineers use finite element analysis or classical beam theory to model the floor plate's behavior. Key factors influencing the deflection limit include:
- Material properties: The type of material used for the floor plate, such as steel, concrete, or composite materials, affects its stiffness and strength.
- Plate thickness: The thickness of the floor plate plays a significant role in determining its load-carrying capacity and deflection.
- Support conditions: The type of support provided to the floor plate, such as simple supports or fixed supports, influences its deflection and stress distribution.
Deflection Limit Criteria
The deflection limit criteria for floor plates are typically based on serviceability and ultimate limit states. These criteria ensure that the floor plate can withstand normal loads without excessive deflection or damage. The deflection limit is often expressed as a ratio of the deflection to the span length of the floor plate. Key deflection limit criteria include:
- Maximum deflection: The maximum allowable deflection of the floor plate under normal loads.
- Deflection ratio: The ratio of the deflection to the span length of the floor plate.
- Stress limit: The maximum allowable stress in the floor plate under normal loads.
Calculation of Deflection Limit
Calculating the deflection limit of a floor plate involves using mathematical models or numerical methods to analyze the plate's behavior under various loads. Engineers use computer software or hand calculations to determine the deflection and stress distribution in the floor plate. Key calculation methods include:
- Finite element method: A numerical method used to analyze the behavior of complex structures like floor plates.
- Classical beam theory: A mathematical model used to analyze the behavior of simple beam structures.
- Plate theory: A mathematical model used to analyze the behavior of plate structures.
Factors Influencing Deflection Limit
Several factors influence the deflection limit of a floor plate, including material properties, plate thickness, support conditions, and load type. Other factors that can affect the deflection limit include temperature changes, moisture, and corrosion. Key factors influencing deflection limit include:
- Temperature effects: Temperature changes can cause expansion or contraction of the floor plate, affecting its deflection.
- Moisture effects: Moisture can cause corrosion or deterioration of the floor plate, reducing its load-carrying capacity.
- Corrosion effects: Corrosion can reduce the strength and stiffness of the floor plate, increasing its deflection.
Consequences of Exceeding Deflection Limit
Exceeding the deflection limit of a floor plate can have severe consequences, including collapse, damage to adjacent structures, and injuries to occupants. Key consequences of exceeding deflection limit include:
- Collapse: Exceeding the deflection limit can cause the floor plate to collapse, resulting in catastrophic failure.
- Damage to adjacent structures: Exceeding the deflection limit can cause damage to adjacent structures, such as walls or columns.
- Injuries to occupants: Exceeding the deflection limit can cause injuries to occupants, particularly if the floor plate collapses or fails suddenly.
How do you calculate deflection rate?
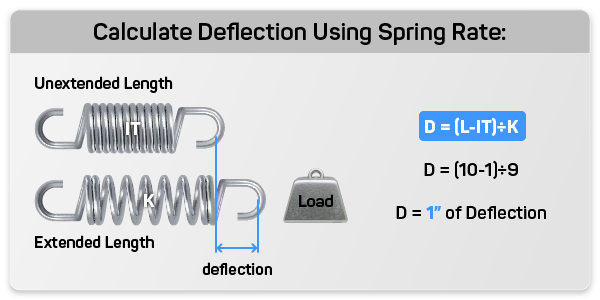
To calculate the deflection rate, you need to understand the concept of deflection, which refers to the change in direction or trajectory of an object or a system. In various fields such as engineering, physics, and materials science, deflection is a critical parameter that determines the performance and stability of structures, beams, or other components. The deflection rate is essentially the measure of how much an object or a system deflects under a given load or force.
Understanding Deflection and Its Importance
Deflection is a critical parameter in design and analysis, especially in structural engineering and materials science. It helps in understanding how different materials and structures behave under various loads. To calculate the deflection rate, one must first understand the type of load applied (e.g., point load, uniformly distributed load) and the properties of the material (e.g., Young's modulus, Poisson's ratio). The calculation involves using formulas that relate the load, material properties, and the geometry of the structure to the resulting deflection. The key steps include:
- Identifying the type of load and its magnitude
- Determining the material properties
- Applying the appropriate deflection formula based on the load and structure
Formulas for Calculating Deflection
The formulas for calculating deflection vary depending on the type of structure (e.g., beam, column) and the load applied. For a simple beam under a point load, the deflection at the point of load application can be calculated using the formula ( delta = frac{PL^3}{3EI} ), where ( delta ) is the deflection, ( P ) is the load, ( L ) is the length of the beam, ( E ) is the modulus of elasticity (Young's modulus), and ( I ) is the moment of inertia of the beam's cross-section. For more complex scenarios, such as uniformly distributed loads or different types of boundary conditions, other formulas must be used. The steps to apply these formulas include:
- Selecting the correct formula based on the load and boundary conditions
- Plugging in the known values for load, length, modulus of elasticity, and moment of inertia
- Solving for the deflection
Role of Material Properties
The material properties, such as Young's modulus and Poisson's ratio, play a crucial role in determining the deflection of a structure. Young's modulus is a measure of the stiffness of a material, and Poisson's ratio relates the lateral strain to the axial strain. These properties are essential in calculating the deflection because they define how a material will respond to a load. For instance, a material with a high Young's modulus will deflect less under the same load compared to a material with a lower Young's modulus. Understanding these properties is vital for:
- Material selection for a specific application
- Designing structures to minimize or maximize deflection as needed
- Predicting the behavior of structures under various loads
Impact of Load Type and Magnitude
The type and magnitude of the load significantly affect the deflection of a structure. Different load types, such as point loads, uniformly distributed loads, and moment loads, will result in different deflection patterns. Furthermore, the magnitude of the load directly impacts the amount of deflection; a larger load will typically result in greater deflection. Understanding the load conditions is essential for:
- Determining the appropriate calculation method for deflection
- Designing structures that can safely support the expected loads
- Assessing the safety and performance of existing structures under new or changed load conditions
Applications and Limitations of Deflection Calculations
Deflection calculations have pr!actical applications in various fields, including civil engineering, mechanical engineering, and aerospace engineering. These calculations are used to design and analyze bridges, buildings, aircraft, and many other structures. However, there are also limitations to these calculations, such as assumptions about the material behavior and the simplifications used in the models. It's important to consider:
- The assumptions and simplifications inherent in the calculation methods
- The potential for non-linear behavior under certain conditions
- The need for experimental validation of calculated deflections in some cases
Frequently Asked Questions (FAQs)
What is the Flat Plate Deflection Calculator and how does it work?
The Flat Plate Deflection Calculator is a tool used to calculate the deflection of a flat plate under various types of loads, such as uniformly distributed loads, point loads, and moment loads. This calculator is based on the theory of plates, which is a fundamental concept in mechanics of materials and structural engineering. The calculator takes into account the material properties, such as the modulus of elasticity and Poisson's ratio, as well as the plate dimensions and boundary conditions. By inputting these values, the calculator can determine the maximum deflection of the plate, which is an essential parameter in designing and analyzing structural systems.
What are the different types of loads that can be applied to the Flat Plate Deflection Calculator?
The Flat Plate Deflection Calculator can handle various types of loads, including uniformly distributed loads, point loads, and moment loads. Uniformly distributed loads are loads that are evenly distributed over the entire surface of the plate, such as a weight or pressure. Point loads, on the other hand, are loads that are applied at a single point on the plate, such as a force or moment. Moment loads are loads that cause a rotation or bending of the plate, such as a torque or twist. The calculator can also handle combinations of these loads, allowing users to simulate real-world scenarios and complex loading conditions. By applying these different types of loads, users can analyze the behavior of the plate and determine the optimal design for their specific application.
What are the key factors that affect the deflection of a flat plate?
The deflection of a flat plate is affected by several key factors, including the material properties, plate dimensions, and boundary conditions. The material properties, such as the modulus of elasticity and Poisson's ratio, play a significant role in determining the stiffness and flexibility of the plate. The plate dimensions, including the length, width, and thickness, also impact the deflection of the plate. The boundary conditions, such as the support and constraint conditions, can also significantly affect the deflection of the plate. Additionally, the load type and magnitude also influence the deflection of the plate. By understanding these key factors, users can optimize the design of their flat plate and minimize the deflection to achieve the desired performance and safety.
How can the Flat Plate Deflection Calculator be used in real-world applications?
The Flat Plate Deflection Calculator has numerous real-world applications in various fields, including civil engineering, mechanical engineering, and aerospace engineering. The calculator can be used to design and analyze structural systems, such as buildings, bridges, and aircraft. It can also be used to optimize the performance of machine components, such as gears, bearings, and shafts. Additionally, the calculator can be used to simulate complex loading conditions and failure modes, allowing users to predict and prevent potential failures. By using the Flat Plate Deflection Calculator, users can save time and resources by reducing the need for physical prototypes and experimental testing. The calculator can also help users to ensure compliance with industry standards and regulations, such as ASME and ASTM.
Deja una respuesta

Entradas Relacionadas