Division of Lengths, Composite Length Formulas and Calculators

When working with lengths and measurements, it is essential to understand how to divide and combine them accurately. Division of lengths involves splitting a given length into equal or unequal parts, while composite length formulas provide a way to calculate the total length of complex shapes. Utilizing calculators and formulas, individuals can simplify these processes and achieve precise results. This article will delve into the concepts of dividing lengths, exploring composite length formulas, and examining the role of calculators in facilitating these calculations, providing a comprehensive overview of these fundamental principles. Accurate calculations are crucial in various fields.
- Understanding Division of Lengths, Composite Length Formulas, and Calculators
- What is the formula for a composite figure?
- How do you divide composite figures?
- How do you find the length of a composite figure?
- How do you find the area of a geometric figure?
-
Frequently Asked Questions (FAQs)
- What are the advantages of using composite length formulas in geometry and engineering?
- How do calculators facilitate the division of lengths and application of composite length formulas?
- What are the common applications of composite length formulas in real-world scenarios?
- How do different units and scales affect the application of composite length formulas?
Understanding Division of Lengths, Composite Length Formulas, and Calculators
The division of lengths, composite length formulas, and calculators are essential tools in various fields such as physics, engineering, and mathematics. These concepts help us understand and work with different units of measurement, convert between them, and perform calculations with precision. In this context, length refers to the measure of distance between two points, and division involves splitting a length into smaller parts or comparing it to another length.
Introduction to Length Units and Conversion
When dealing with lengths, it's crucial to understand the different units of measurement and how to convert between them. The most common length units are meters, feet, inches, and miles. Conversion between these units is necessary to ensure accuracy in calculations and measurements. For instance, to convert meters to feet, we multiply the length in meters by 3.2808.
Composite Length Formulas and Calculations
Composite length formulas involve combining two or more lengths to find a new length. This can be done using addition, subtraction, multiplication, or division. For example, to find the total length of two objects, we add their individual lengths together. In calculations, it's essential to use the correct unit conversions and formulas to ensure accuracy.
Calculators for Length Calculations
Calculators are valuable tools for performing length calculations quickly and accurately. They can be used for unit conversions, composite length calculations, and division of lengths. Online calculators and software are also available, offering advanced features and precision in calculations.
Applications of Length Calculations and Formulas
Length calculations and formulas have numerous applications in various fields. In physics, they are used to calculate distances, velocities, and accelerations. In engineering, they are essential for designing and building structures, roads, and bridges. In mathematics, length calculations are used to solve problems involving geometry and trigonometry.
Common Errors in Length Calculations and Formulas
Common errors in length calculations and formulas include unit conversion errors, formula mistakes, and rounding errors. To avoid these errors, it's essential to use the correct unit conversions, formulas, and calculation techniques. Double-checking calculations and conversions can also help prevent errors.
| Length Unit | Conversion Factor | Description |
|---|---|---|
| Meter | 1 meter = 3.2808 feet | Basic unit of length in the metric system |
| Foot | 1 foot = 0.3048 meters | Unit of length in the imperial system |
| Inch | 1 inch = 0.0254 meters | Unit of length in the imperial system |
| Mile | 1 mile = 1609.34 meters | Unit of length for long distances |
What is the formula for a composite figure?
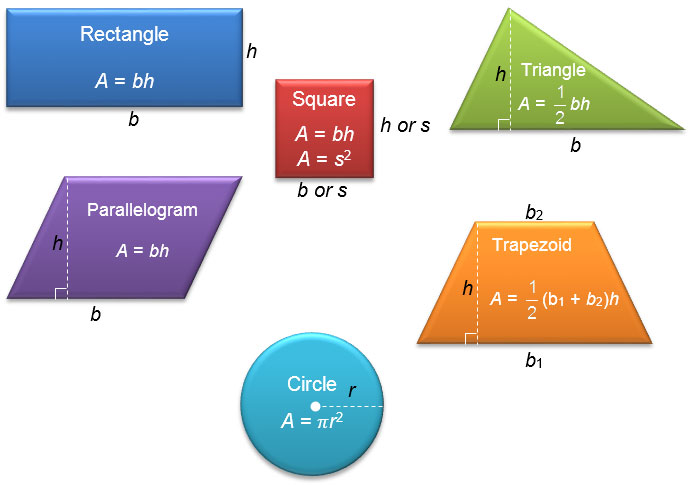
The formula for a composite figure is the sum of the areas of the individual shapes that make up the figure. To find the area of a composite figure, you need to break it down into its individual components, such as rectangles, triangles, and circles, and then calculate the area of each component separately.
Understanding Composite Figures
Composite figures are made up of multiple individual shapes, and to find their area, you need to understand the geometry of each component. This involves identifying the length, width, and height of each shape, as well as the radius of any circles. Once you have this information, you can use the relevant formulas to calculate the area of each shape.
- Identify the individual shapes that make up the composite figure
- Calculate the area of each shape using the relevant formulas
- Add up the areas of all the shapes to find the total area of the composite figure
Formulas for Individual Shapes
To calculate the area of a composite figure, you need to know the formulas for the individual shapes that make it up. The formula for the area of a rectangle is length x width, while the formula for the area of a triangle is (base x height) / 2. The formula for the area of a circle is πr^2, where r is the radius of the circle.
- Rectangle: length x width
- Triangle: (base x height) / 2
- Circle: πr^2
Breaking Down Composite Figures
To find the area of a composite figure, you need to break it down into its individual components. This involves identifying the shapes that make up the figure and calculating the area of each shape separately. You can then add up the areas of all the shapes to find the total area of the composite figure.
- Identify the individual shapes that make up the composite figure
- Calculate the area of each shape using the relevant formulas
- Add up the areas of all the shapes to find the total area of the composite figure
Applying the Formulas
Once you have broken down the composite figure into its individual components, you can apply the relevant formulas to calculate the area of each shape. This involves plugging in the values for the length, width, height, and radius of each shape into the relevant formulas.
- Plug in the values for the length, width, height, and radius of each shape into the relevant formulas
- Calculate the area of each shape using the formulas
- Add up the areas of all the shapes to find the total area of the composite figure
Calculating the Total Area
To find the total area of a composite figure, you need to add up the areas of all the individual shapes that make it up. This involves calculating the area of each shape using the relevant formulas and then adding up the results. The total area of the composite figure is the sum of the areas of all the individual shapes.
- Calculate the area of each shape using the relevant formulas
- Add up the areas of all the shapes to find the total area of the composite figure
- Check your calculation to make sure it is accurate
How do you divide composite figures?
To divide composite figures, you need to break them down into simpler shapes, such as rectangles, triangles, and circles. This is because composite figures are made up of multiple simpler shapes, and by dividing them into these simpler shapes, you can calculate their area and perimeter more easily. For example, a composite figure made up of two rectangles and a triangle can be divided into these three simpler shapes, and then the area and perimeter of each shape can be calculated separately.
Understanding the Basics of Composite Figures
To divide composite figures, you need to understand the basics of geometry and how to calculate the area and perimeter of different shapes. This includes understanding the formulas for the area and perimeter of rectangles, triangles, and circles, as well as how to apply these formulas to more complex composite figures. Here are some key points to consider:
- Identify the individual shapes that make up the composite figure, such as rectangles, triangles, and circles.
- Calculate the area and perimeter of each individual shape using the relevant formulas.
- Combine the areas and perimeters of the individual shapes to find the total area and perimeter of the composite figure.
Breaking Down Composite Figures into Simpler Shapes
Breaking down composite figures into simpler shapes is a crucial step in dividing them. This involves identifying the individual shapes that make up the composite figure, such as rectangles, triangles, and circles, and then calculating their area and perimeter separately. For example, a composite figure made up of two rectangles and a triangle can be broken down into these three simpler shapes, and then the area and perimeter of each shape can be calculated separately. Here are some key points to consider:
- Identify the individual shapes that make up the composite figure, such as rectangles, triangles, and circles.
- Draw a diagram of the composite figure and label each individual shape.
- Calculate the area and perimeter of each individual shape using the relevant formulas.
Calculating the Area of Composite Figures
Calculating the area of composite figures involves calculating the area of each individual shape that makes up the figure, and then combining these areas to find the total area. For example, if a composite figure is made up of two rectangles and a triangle, you would calculate the area of each rectangle and the triangle separately, and then add these areas together to find the total area. Here are some key points to consider:
- Calculate the area of each individual shape using the relevant formulas, such as length x width for rectangles.
- Combine the areas of the individual shapes to find the total area of the composite figure.
- Use units such as square meters or square feet to express the area of the composite figure.
Calculating the Perimeter of Composite Figures
Calculating the perimeter of composite figures involves calculating the perimeter of each individual shape that makes up the figure, and then combining these perimeters to find the total perimeter. For example, if a composite figure is made up of two rectangles and a triangle, you would calculate the perimeter of each rectangle and the triangle separately, and then add these perimeters together to find the total perimeter. Here are some key points to consider:
- Calculate the perimeter of each individual shape using the relevant formulas, such as 2 x length + 2 x width for rectangles.
- Combine the perimeters of the individual shapes to find the total perimeter of the composite figure.
- Use units such as meters or feet to express the perimeter of the composite figure.
Real-World Applications of Dividing Composite Figures
Dividing composite figures has many real-world applications, such as architecture, engineering, and design. For example, architects use composite figures to design buildings and calculate their area and perimeter, while engineers use composite figures to design bridges and calculate their stress and strain. Here are some key points to consider:
- Use composite figures to design and calculate the area and perimeter of buildings and other structures.
- Apply mathematical formulas to calculate the stress and strain on composite figures, such as bridges and buildings.
- Use computer-aided design software to create and manipulate composite figures, and to calculate their area and perimeter.
How do you find the length of a composite figure?

To find the length of a composite figure, you need to break it down into its individual components, such as rectangles, triangles, and circles. Then, calculate the perimeter of each component and add them together to find the total length. This process involves identifying the different shapes that make up the composite figure, calculating their individual dimensions, and combining them to find the overall length.
Understanding Composite Figures
To find the length of a composite figure, you need to understand what composite figures are and how they are created. A composite figure is a shape that is made up of multiple simpler shapes, such as rectangles, triangles, and circles. To work with composite figures, you need to break them down into their individual components and calculate their perimeters. Here are the steps to follow:
- Identify the individual components of the composite figure, such as rectangles, triangles, and circles.
- Calculate the perimeter of each component using the relevant formulas, such as 2(l + w) for a rectangle or 3s for an equilateral triangle.
- Add the perimeters of the individual components together to find the total length of the composite figure.
Calculating Perimeters of Components
To calculate the perimeter of each component, you need to know the relevant formulas. For example, the perimeter of a rectangle is given by 2(l + w), where l is the length and w is the width. The perimeter of a triangle is given by 3s, where s is the length of one of its sides. For a circle, the circumference is given by 2πr, where r is the radius. Here are some key points to keep in mind:
- Use the relevant formulas to calculate the perimeter of each component, such as 2(l + w) for a rectangle or 3s for an equilateral triangle.
- Make sure to use the correct units, such as inches or centimeters, when calculating the perimeter.
- Be careful when working with circles, as the circumference formula involves π and can be tricky to calculate.
Breaking Down Complex Shapes
Breaking down complex shapes into their individual components can be challenging. To do this, you need to identify the different shapes that make up the composite figure and calculate their perimeters. For example, a complex shape might consist of a rectangle with a triangle attached to it. To find the total length, you need to calculate the perimeter of the rectangle and the triangle separately and then add them together. Here are some tips to keep in mind:
- Use visual aids, such as diagrams, to help break down complex shapes into their individual components.
- Identify the different shapes that make up the composite figure, such as rectangles, triangles, and circles.
- Use the relevant formulas to calculate the perimeter of each component, such as 2(l + w) for a rectangle or 3s for an equilateral triangle.
Combining Perimeters
Once you have calculated the perimeter of each component, you need to combine them to find the total length of the composite figure. This involves adding the perimeters of the individual components together. For example, if a composite figure consists of a rectangle with a perimeter of 10 inches and a triangle with a perimeter of 6 inches, the total length would be 10 + 6 = 16 inches. Here are some key points to keep in mind:
- Add the perimeters of the individual components together to find the total length of the composite figure.
- Make sure to use the correct units, such as inches or centimeters, when combining the perimeters.
- Be careful when working with circles, as the circumference formula involves π and can be tricky to calculate.
Real-World Applications
Finding the length of a composite figure has many real-world applications, such as architecture, engineering, and design. For example, architects need to calculate the perimeter of buildings and other structures to determine the amount of materials needed for construction. Engineers need to calculate the perimeter of machinery and other equipment to determine their efficiency and performance. Here are some examples of real-world applications:
- Architecture: calculating the perimeter of buildings and other structures to determine the amount of materials needed for construction.
- Engineering: calculating the perimeter of machinery and other equipment to determine their efficiency and performance.
- Design: calculating the perimeter of products and other objects to determine their aesthetics and functionality.
How do you find the area of a geometric figure?
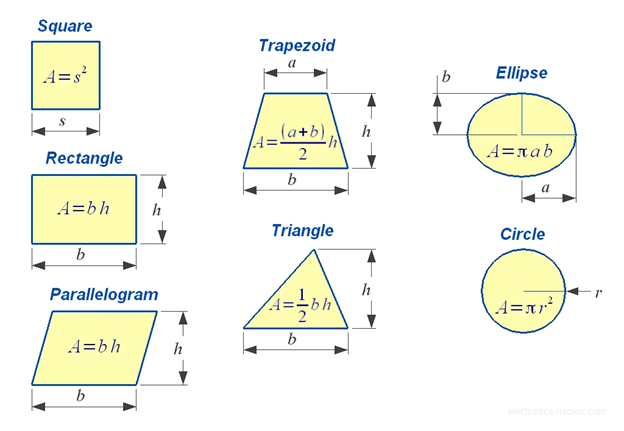
To find the area of a geometric figure, you need to use different formulas depending on the type of figure. For example, the area of a rectangle is calculated by multiplying the length and width, while the area of a circle is calculated using the formula πr^2, where r is the radius. The area of a triangle can be calculated using the formula 1/2bh, where b is the base and h is the height.
Understanding Geometric Figures
Understanding the different types of geometric figures is crucial in calculating their area. Different figures have different formulas and techniques for calculating their area. For example, polygons can be divided into triangles and rectangles to calculate their area, while circles and ellipses require the use of pi and trigonometric functions. Some key points to consider when understanding geometric figures include:
- Vertices: The points where the sides of a figure meet.
- Edges: The lines that connect the vertices of a figure.
- Faces: The surfaces of a three-dimensional figure.
Formulas for Calculating Area
There are many different formulas for calculating the area of geometric figures. For example, the area of a rectangle is calculated by multiplying the length and width, while the area of a circle is calculated using the formula πr^2, where r is the radius. Some key formulas to remember include:
- Rectangle: Area = length x width.
- Circle: Area = πr^2.
- Triangle: Area = 1/2 x base x height.
Techniques for Calculating Area
There are several techniques for calculating the area of geometric figures. For example, decomposition involves dividing a figure into simpler shapes, such as triangles and rectangles, to calculate its area. Transformation involves changing the shape or size of a figure to calculate its area. Some key techniques to consider include:
- Decomposition: Dividing a figure into simpler shapes.
- Transformation: Changing the shape or size of a figure.
- Approximation: Using estimates or approximations to calculate the area of a figure.
Applications of Area Calculation
Calculating the area of geometric figures has many practical applications. For example, architects use area calculations to design buildings and engineers use area calculations to design systems and structures. Artists and designers also use area calculations to create compositions and layouts. Some key applications to consider include:
- Architecture: Designing buildings and structures.
- Engineering: Designing systems and structures.
- Art and Design: Creating compositions and layouts.
Calculating Area with Technology
With the advent of technology, calculating the area of geometric figures has become easier and more accurate. Computer-aided design (CAD) software and graphing calculators can be used to calculate the area of complex figures. Online tools and apps can also be used to calculate the area of figures. Some key technologies to consider include:
- CAD Software: Computer-aided design software.
- Graphing Calculators: Calculators that can graph and calculate area.
- Online Tools and Apps: Online tools and apps that can calculate area.
Frequently Asked Questions (FAQs)
What are the advantages of using composite length formulas in geometry and engineering?
The use of composite length formulas in geometry and engineering offers several advantages, including increased accuracy and precision in calculations. These formulas allow for the combination of different length measurements, taking into account various factors such as units, scales, and proportions. By using composite length formulas, engineers and geometers can simplify complex calculations, reducing the margin of error and increasing the reliability of their results. Furthermore, these formulas enable the comparison of different length measurements, facilitating the identification of patterns and trends in geometric shapes and engineering structures. The application of composite length formulas is essential in various fields, including architecture, construction, and manufacturing, where precise length measurements are crucial for design, planning, and execution.
How do calculators facilitate the division of lengths and application of composite length formulas?
Calculators play a significant role in facilitating the division of lengths and the application of composite length formulas. These electronic devices enable users to perform complex calculations quickly and accurately, reducing the time and effort required to obtain results. Calculators often feature built-in functions and formulas for length conversions, proportions, and scaling, making it easier to apply composite length formulas. Additionally, calculators can store and recall previously calculated values, allowing users to reference and compare different length measurements. The use of calculators also reduces the risk of human error, as they can perform calculations with high precision and accuracy. Moreover, specialized calculators are available for specific fields, such as engineering and architecture, which provide customized functions and formulas tailored to the needs of these professions.
What are the common applications of composite length formulas in real-world scenarios?
Composite length formulas have numerous practical applications in various fields, including engineering, architecture, construction, and manufacturing. In building design, these formulas are used to calculate the lengths of beams, columns, and foundations, ensuring that the structure is stable and safe. In mechanical engineering, composite length formulas are applied to calculate the lengths of shafts, gears, and pulleys, which is crucial for the functionality and efficiency of machines. In surveying and mapping, these formulas are used to calculate the lengths of boundaries, distances, and elevations, providing accurate and precise information for land planning and development. Furthermore, composite length formulas are used in quality control and inspections, where accurate length measurements are essential for evaluating the compliance of products with industry standards.
How do different units and scales affect the application of composite length formulas?
The units and scales used in composite length formulas can significantly impact the accuracy and reliability of calculations. Different units, such as metric and imperial, require conversions and transformations, which can introduce errors if not performed correctly. Similarly, scales, such as ratio and proportion, must be considered when applying composite length formulas. Inconsistent or inaccurate scaling can lead to incorrect results, which can have serious consequences in engineering and architecture. To mitigate these risks, it is essential to use consistent and accurate units and scales, and to apply composite length formulas with caution and attention to detail. Additionally, understanding the relationships between different units and scales is crucial for applying composite length formulas effectively in various fields.
Deja una respuesta


Entradas Relacionadas