Division of Lengths and Spacing Formulas and Calculators
The division of lengths and spacing formulas are essential tools in various fields, including architecture, engineering, and design. Calculators and formulas enable the precise calculation of lengths and spacings, ensuring accuracy and efficiency in projects. This article will delve into the world of division of lengths and spacing formulas, exploring their applications, benefits, and uses, and providing access to calculators and formulas to facilitate calculations and problem-solving. With practical examples and explanations, readers will gain a deeper understanding of these fundamental concepts and their real-world applications. Calculators and formulas will be provided for reference.
- Division of Lengths and Spacing Formulas and Calculators
- How to calculate center to center spacing?
-
Frequently Asked Questions (FAQs)
- What are the main concepts involved in the division of lengths and spacing formulas and calculators?
- How do division of lengths and spacing formulas and calculators apply to real-world problems?
- What are some common challenges and limitations when working with division of lengths and spacing formulas and calculators?
- How can I improve my skills and knowledge in using division of lengths and spacing formulas and calculators?
Division of Lengths and Spacing Formulas and Calculators
The division of lengths and spacing formulas and calculators are essential tools in various fields such as engineering, architecture, and design. These tools enable users to calculate and divide lengths, spaces, and areas with precision and accuracy. The division of lengths and spacing formulas and calculators can be applied to various scenarios, including the division of rooms, buildings, and other structures. The use of these tools can help to optimize space, reduce waste, and improve the overall efficiency of a project.
Introduction to Division of Lengths and Spacing Formulas
The division of lengths and spacing formulas is based on mathematical equations that take into account the dimensions and proportions of a given space or object. These formulas can be used to divide a length or space into equal parts, or to calculate the spacing between objects or elements. The division of lengths and spacing formulas can be applied to various types of measurements, including linear measurements, area measurements, and volume measurements.
Types of Division of Lengths and Spacing Formulas
There are various types of division of lengths and spacing formulas, including proportional division, equal division, and unequal division. Proportional division involves dividing a length or space into parts that are proportional to each other. Equal division involves dividing a length or space into equal parts. Unequal division involves dividing a length or space into parts that are not equal.
Applications of Division of Lengths and Spacing Formulas
The division of lengths and spacing formulas has various applications in fields such as engineering, architecture, and design. These formulas can be used to calculate the spacing between columns, beams, and other structural elements in a building. They can also be used to calculate the area of rooms, corridors, and other spaces in a building.
Division of Lengths and Spacing Calculators
Division of lengths and spacing calculators are tools that can be used to calculate and divide lengths, spaces, and areas with precision and accuracy. These calculators can be in the form of software programs, mobile apps, or online tools. They can be used to calculate various types of measurements, including linear measurements, area measurements, and volume measurements.
Benefits of Using Division of Lengths and Spacing Formulas and Calculators
The use of division of lengths and spacing formulas and calculators can provide various benefits, including improved accuracy, increased efficiency, and reduced waste. These tools can help to optimize space, reduce errors, and improve the overall quality of a project. The following table highlights the benefits of using division of lengths and spacing formulas and calculators:
| Benefit | Description |
|---|---|
| Improved Accuracy | The use of division of lengths and spacing formulas and calculators can help to improve the accuracy of measurements and calculations. |
| Increased Efficiency | The use of division of lengths and spacing formulas and calculators can help to increase the efficiency of a project by reducing the time and effort required to complete tasks. |
| Reduced Waste | The use of division of lengths and spacing formulas and calculators can help to reduce waste by optimizing the use of materials and resources. |
How to calculate center to center spacing?
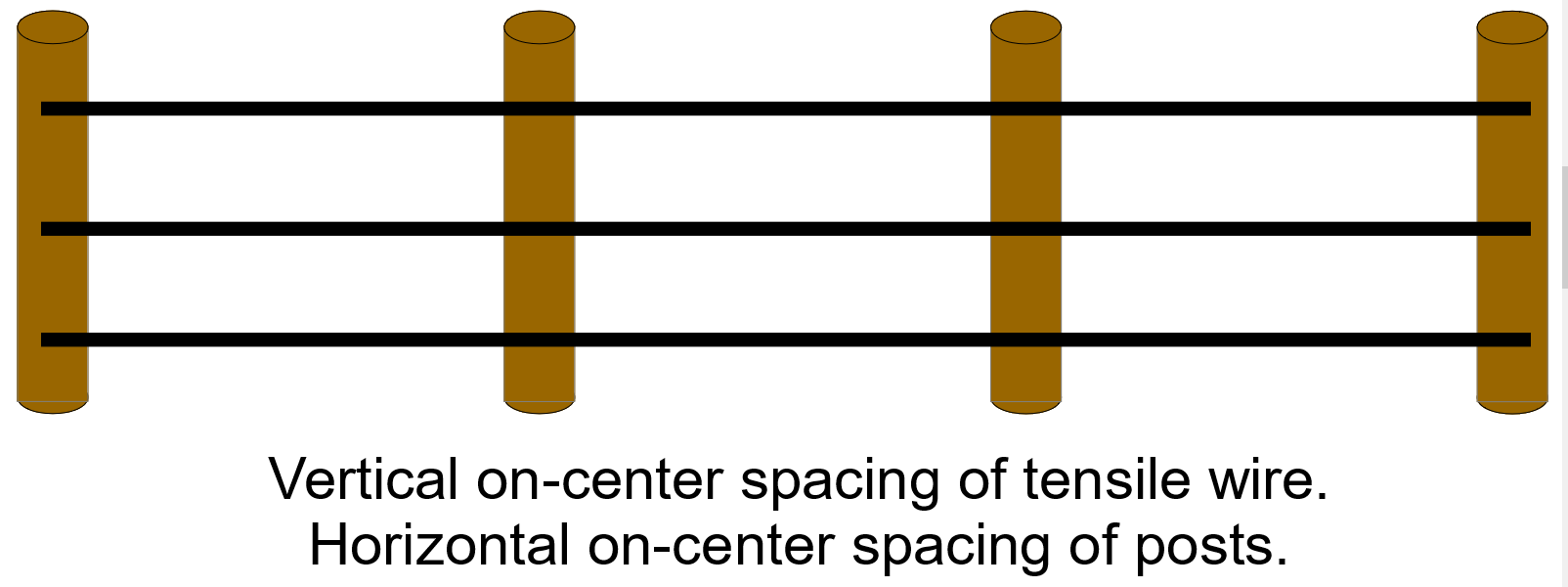
To calculate center to center spacing, you need to understand the concept of spacing and how it applies to different objects or components. Center to center spacing refers to the distance between the centers of two objects, which is a crucial aspect of design and engineering. This calculation is essential in various fields, including architecture, engineering, and product design, where precise spacing is necessary to ensure proper functioning, stability, and aesthetics.
Understanding the Concept of Center to Center Spacing
The concept of center to center spacing is straightforward, yet it requires careful consideration of the objects' dimensions and positions. To calculate this spacing, you need to know the dimensions of the objects, including their width, length, and height. The calculation involves finding the distance between the center points of the two objects, which can be done using basic geometric formulas. The key steps involve:
- Identifying the center points of the objects, which can be done by finding the midpoint of each object's dimensions.
- Calculating the distance between the center points, which can be done using the distance formula or Pythagorean theorem.
- Considering any offsets or gaps between the objects, which can affect the overall spacing.
Applications of Center to Center Spacing
Center to center spacing has numerous applications in various fields, including architecture, engineering, and product design. In architecture, precise spacing is crucial for ensuring structural integrity and aesthetic appeal. In engineering, center to center spacing is essential for designing mechanisms and systems that require precise movement and alignment. The applications of center to center spacing include:
- Building design, where precise spacing ensures structural stability and aesthetic appeal.
- Machine design, where center to center spacing is crucial for ensuring proper movement and alignment.
- Product design, where precise spacing affects the usability and ergonomics of a product.
Calculating Center to Center Spacing for Circular Objects
Calculating center to center spacing for circular objects requires a different approach than for rectangular objects. The calculation involves finding the distance between the centers of the two circles, which can be done using the distance formula or Pythagorean theorem. The key steps involve:
- Identifying the center points of the circles, which can be done by finding the midpoint of each circle's diameter.
- Calculating the distance between the center points, which can be done using the distance formula or Pythagorean theorem.
- Considering any overlaps or gaps between the circles, which can affect the overall spacing.
Calculating Center to Center Spacing for Rectangular Objects
Calculating center to center spacing for rectangular objects involves finding the distance between the centers of the two objects, which can be done using basic geometric formulas. The calculation involves:
- Identifying the center points of the objects, which can be done by finding the midpoint of each object's width and length.
- Calculating the distance between the center points, which can be done using the distance formula or Pythagorean theorem.
- Considering any offsets or gaps between the objects, which can affect the overall spacing.
Common Mistakes in Calculating Center to Center Spacing
Common mistakes in calculating center to center spacing include measurement errors, calculation mistakes, and ignoring offsets or gaps. To avoid these mistakes, it's essential to:
- Double-check measurements to ensure accuracy.
- Use precise calculation methods, such as the distance formula or Pythagorean theorem.
- Consider all relevant factors, including offsets, gaps, and overlaps.
Frequently Asked Questions (FAQs)
What are the main concepts involved in the division of lengths and spacing formulas and calculators?
The division of lengths and spacing formulas and calculators involve several key concepts, including measurement units, proportions, and ratios. To understand these concepts, it's essential to have a solid grasp of mathematical principles, such as algebra and geometry. When working with lengths and spacing, you'll need to consider factors like scale, resolution, and precision to ensure accurate calculations and results. Additionally, familiarity with calculators and software tools can help streamline the process and reduce errors. By mastering these concepts and tools, you'll be able to tackle complex problems and make informed decisions in various fields, from architecture and engineering to design and manufacturing.
How do division of lengths and spacing formulas and calculators apply to real-world problems?
The division of lengths and spacing formulas and calculators have numerous practical applications in various industries and fields. For instance, in construction and architecture, these formulas and calculators are used to determine the optimal spacing of building components, such as columns, beams, and joists. In manufacturing, they're used to calculate the dimensions and tolerances of parts and components, ensuring precise fit and functionality. In design, these formulas and calculators help create aesthetically pleasing and functional layouts, taking into account factors like balance, proportion, and harmony. By applying these mathematical concepts and tools, professionals can create efficient, effective, and sustainable solutions that meet the needs of their clients and users.
What are some common challenges and limitations when working with division of lengths and spacing formulas and calculators?
When working with division of lengths and spacing formulas and calculators, several challenges and limitations can arise. One common issue is unit conversion, where inconsistent units can lead to errors and inaccuracies. Another challenge is rounding errors, which can occur when using approximations or estimates instead of exact values. Additionally, complex calculations can be time-consuming and prone to human error, especially when performed manually. Furthermore, software limitations and compatibility issues can also hinder the use of calculators and other digital tools. To overcome these challenges, it's essential to double-check calculations, use precise units, and verify results to ensure accuracy and reliability. By being aware of these potential pitfalls, you can take steps to mitigate risks and produce high-quality results.
How can I improve my skills and knowledge in using division of lengths and spacing formulas and calculators?
To improve your skills and knowledge in using division of lengths and spacing formulas and calculators, it's essential to practice regularly and apply theoretical concepts to real-world problems. You can start by reviewing mathematical principles and formulas, and then progress to more complex calculations and case studies. Utilizing online resources, such as tutorials, videos, and software tools, can also help you develop your skills and stay up-to-date with the latest technologies and methodologies. Additionally, collaborating with others and joining online communities can provide valuable opportunities for knowledge sharing, feedback, and peer review. By adopting a continuous learning approach and staying committed to your goals, you can become proficient in using division of lengths and spacing formulas and calculators, and achieve success in your chosen field.
Deja una respuesta

Entradas Relacionadas