Discharge Time under Falling Head Formulae and Calculator
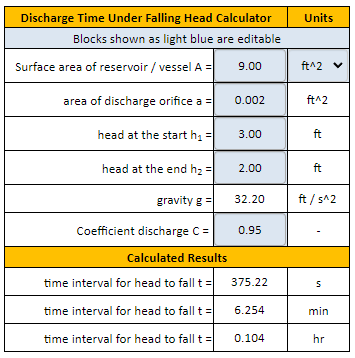
The discharge time under falling head formulae is a crucial concept in hydrology and civil engineering, used to calculate the time it takes for water to drain from a reservoir or tank. This calculation is essential for designing and operating various water management systems, including drainage canals, stormwater detention ponds, and irrigation systems. The formulae take into account the initial and final water levels, as well as the coefficient of discharge, to determine the time required for the water level to fall. A calculator can simplify this process, providing accurate results quickly and efficiently. Accurate calculations are vital.
- Discharge Time under Falling Head Formulae and Calculator
- What is the formula for discharge in terms of time?
- What is the formula for the discharge coefficient?
- What is the formula for theoretical discharge in fluid mechanics?
-
Frequently Asked Questions (FAQs)
- What is the Discharge Time under Falling Head Formulae and Calculator?
- How does the Discharge Time under Falling Head Formulae and Calculator work?
- What are the advantages of using the Discharge Time under Falling Head Formulae and Calculator?
- What are the limitations of the Discharge Time under Falling Head Formulae and Calculator?
Discharge Time under Falling Head Formulae and Calculator
The discharge time under falling head is a critical concept in hydraulics, particularly in the design and operation of water resources systems. It refers to the time it takes for the water level in a reservoir or tank to drop from an initial height to a final height, considering the effects of friction and other losses. The calculation of this time is essential to determine the efficiency of pumps and other hydraulic systems.
Introduction to Discharge Time Formulae
The discharge time under falling head can be calculated using various formulae, which take into account the geometry of the system, the initial and final water levels, and the discharge rate. One commonly used formula is the Torricelli equation, which assumes a frictionless flow and neglects the effects of viscosity. However, in real-world applications, friction and other losses must be considered, and more complex formulae are used.
Factors Affecting Discharge Time
Several factors affect the discharge time under falling head, including the size and shape of the reservoir or tank, the initial and final water levels, the discharge rate, and the friction coefficient. The friction coefficient, in particular, plays a crucial role in determining the efficiency of the system. A higher friction coefficient results in a longer discharge time, while a lower friction coefficient results in a shorter discharge time.
Calculator for Discharge Time
A discharge time calculator is a useful tool for engineers and designers to quickly and accurately determine the discharge time under falling head. These calculators typically require input of the geometry of the system, the initial and final water levels, and the discharge rate. The calculator then uses the formulae to calculate the discharge time, taking into account the effects of friction and other losses.
Applications of Discharge Time Formulae
The discharge time under falling head formulae has numerous applications in water resources engineering, including the design and operation of irrigation systems, water supply systems, and wastewater treatment systems. It is also used in the design of dams and reservoirs, where the discharge time under falling head is critical to determining the stability of the structure.
Limitations and Assumptions
The discharge time under falling head formulae has several limitations and assumptions, including the assumption of a frictionless flow, the neglect of viscosity effects, and the assumption of a constant discharge rate. In reality, friction and viscosity can significantly affect the discharge time, and the discharge rate may vary over time. Therefore, engineers and designers must carefully consider these limitations and assumptions when applying the formulae to real-world problems.
| Formula | Description |
|---|---|
| Torricelli equation | Frictionless flow, neglects viscosity effects |
| Darcy-Weisbach equation | Takes into account friction and viscosity effects |
| Hazen-Williams equation | Empirical formula, widely used in water resources engineering |
What is the formula for discharge in terms of time?

The formula for discharge in terms of time is Q = V/t, where Q is the discharge rate, V is the volume of fluid, and t is the time. This formula is used to calculate the rate at which a fluid flows through a pipe or channel.
Understanding the Concept of Discharge
The concept of discharge is crucial in understanding the behavior of fluids in various systems. Discharge refers to the volume of fluid that flows through a given area per unit of time. To calculate discharge, we need to know the volume of fluid and the time it takes to flow through the system. The formula Q = V/t provides a simple way to calculate discharge, where:
- Q is the discharge rate, typically measured in cubic meters per second (m³/s) or liters per second (L/s)
- V is the volume of fluid, measured in cubic meters (m³) or liters (L)
- t is the time, measured in seconds (s)
Applying the Formula in Real-World Scenarios
The formula Q = V/t has numerous applications in real-world scenarios, such as hydrology, civil engineering, and chemical engineering. For instance, in hydrology, the formula is used to calculate the discharge of a river or stream. In civil engineering, it is used to design pipes and canals to ensure efficient flow of fluids. The formula is also used in chemical engineering to calculate the discharge of fluids in process pipes. Key considerations include:
- Flow rate, which affects the discharge calculation
- Pipe diameter and length, which impact the flow rate and discharge
- Fluid properties, such as density and viscosity, which influence the flow rate and discharge
Factors Affecting Discharge
Several factors can affect the discharge of a fluid, including flow rate, pipe diameter, pipe length, and fluid properties. The formula Q = V/t assumes a constant flow rate, but in reality, flow rate can vary due to factors such as friction, turbulence, and pressure. Additionally, pipe diameter and length can impact the flow rate and discharge. Other factors that can affect discharge include:
- Elevation change, which can impact the pressure and flow rate
- Bends and curves in the pipe, which can cause turbulence and affect flow rate
- Valves and fittings, which can restrict flow rate and impact discharge
Calculating Discharge in Complex Systems
Calculating discharge in complex systems, such as networks of pipes, can be challenging. In such cases, the formula Q = V/t may not be sufficient, and more advanced methods, such as numerical modeling, may be required. These methods take into account the interactions between different components of the system, such as pipes, valves, and pumps. Key considerations in calculating discharge in complex systems include:
- System topology, which affects the flow rate and discharge
- Component characteristics, such as pipe diameter and valve type
- Boundary conditions, such as inlet and outlet conditions
Importance of Accurate Discharge Calculations
Accurate discharge calculations are crucial in various fields, including hydrology, civil engineering, and chemical engineering. Inaccurate calculations can lead to design flaws, operational problems, and environmental hazards. For instance, in hydrology, inaccurate discharge calculations can lead to floods or droughts. In civil engineering, inaccurate calculations can result in pipe failures or water supply issues. To ensure accurate calculations, it is essential to:
- Use reliable data and measurement techniques
- Consider uncertainties and variabilities in the system
- Use validated models and calibration techniques
What is the formula for the discharge coefficient?

The formula for the discharge coefficient is a dimensionless quantity that characterizes the efficiency of a fluid flow system. It is defined as the ratio of the actual flow rate to the theoretical flow rate that would occur if the fluid were flowing through an ideal, frictionless system. The formula for the discharge coefficient is given by: Cd = Q / (A sqrt(2 g h)), where Cd is the discharge coefficient, Q is the actual flow rate, A is the cross-sectional area of the flow, g is the acceleration due to gravity, and h is the head or pressure difference driving the flow.
Derivation of the Discharge Coefficient Formula
The discharge coefficient formula is derived from the equation of continuity and the Bernoulli's equation, which describe the relationship between the velocity and pressure of a fluid in motion. The derivation involves simplifying the equations and making assumptions about the flow, such as steady, incompressible flow with negligible viscosity. The resulting formula provides a quantitative measure of the efficiency of the flow system, allowing designers to optimize the system's performance.
- The equation of continuity states that the mass flow rate of a fluid is constant throughout a flow system.
- The Bernoulli's equation relates the pressure and velocity of a fluid in motion, assuming negligible viscosity and turbulence.
- The discharge coefficient formula is derived by combining these equations and making assumptions about the flow, such as steady, incompressible flow with negligible viscosity.
Factors Affecting the Discharge Coefficient
The discharge coefficient is affected by several factors, including the geometry of the flow system, the properties of the fluid, and the operating conditions. For example, the discharge coefficient can be affected by the shape and size of the flow passages, the surface roughness of the flow system, and the velocity and pressure of the fluid. Understanding these factors is crucial for designing and optimizing flow systems.
- The geometry of the flow system, including the shape and size of the flow passages, can significantly affect the discharge coefficient.
- The properties of the fluid, such as its viscosity and density, can also impact the discharge coefficient.
- The operating conditions, including the velocity and pressure of the fluid, can influence the discharge coefficient and the overall performance of the flow system.
Applications of the Discharge Coefficient
The discharge coefficient has numerous applications in various fields, including aerospace engineering, chemical engineering, and civil engineering. It is used to design and optimize flow systems, such as pipes, turbines, and pumps, and to predict the performance of these systems under different operating conditions. The discharge coefficient is also used to model and simulate complex flow systems, allowing designers to test and optimize their designs before building physical prototypes.
- The discharge coefficient is used in aerospace engineering to design and optimize the flow systems of aircraft and spacecraft.
- In chemical engineering, the discharge coefficient is used to design and optimize process equipment, such as pipes and turbines.
- In civil engineering, the discharge coefficient is used to design and optimize water supply systems, sewage systems, and irrigation systems.
Measurement of the Discharge Coefficient
The discharge coefficient can be measured experimentally using various techniques, including flow metering and pressure measurement. These techniques involve measuring the flow rate and pressure of the fluid at different points in the flow system and using these measurements to calculate the discharge coefficient. The measurements can be made using sensors and data acquisition systems, which provide accurate and reliable data.
- Flow metering involves measuring the flow rate of the fluid using devices such as turbine meters or ultrasonic meters.
- Pressure measurement involves measuring the pressure of the fluid at different points in the flow system using devices such as pressure sensors or manometers.
- Data acquisition systems are used to collect and analyze the data from the measurements, providing accurate and reliable values of the discharge coefficient.
Limitations and Assumptions of the Discharge Coefficient Formula
The discharge coefficient formula is based on several assumptions and limitations, including the assumption of steady, incompressible flow with negligible viscosity and turbulence. These assumptions can limit the accuracy of the formula in certain situations, such as high-velocity flows or flows with complex geometries. Additionally, the formula does not account for energy losses due to friction or heat transfer, which can also impact the accuracy of the results.
- The discharge coefficient formula assumes steady, incompressible flow with negligible viscosity and turbulence.
- The formula does not account for energy losses due to friction or heat transfer, which can impact the accuracy of the results.
- The complexity of the flow geometry can also limit the accuracy of the formula, particularly in situations with high-velocity flows or turbulent flows.
What is the formula for theoretical discharge in fluid mechanics?

The formula for theoretical discharge in fluid mechanics is given by the equation Q = A v, where Q is the discharge, A is the cross-sectional area of the flow, and v is the velocity of the fluid. This equation is a fundamental concept in fluid mechanics and is used to calculate the rate at which fluid flows through a pipe or channel.
Introduction to Discharge Formula
The discharge formula is a simple yet powerful tool for calculating the rate of fluid flow. It is widely used in various fields such as civil engineering, mechanical engineering, and environmental engineering. The formula is based on the principle that the rate of fluid flow is equal to the product of the cross-sectional area of the flow and the velocity of the fluid. Some key points to note about the discharge formula are:
- The cross-sectional area of the flow must be measured perpendicular to the direction of flow.
- The velocity of the fluid must be measured at the point of interest.
- The discharge formula assumes a steady-state flow, meaning that the flow rate is constant over time.
Factors Affecting Discharge
There are several factors that can affect the discharge of a fluid, including viscosity, density, and friction. The viscosity of the fluid can affect the discharge by creating resistance to flow, while the density of the fluid can affect the discharge by changing the weight of the fluid. Friction can also affect the discharge by creating resistance to flow at the walls of the pipe or channel. Some key factors to consider when calculating discharge are:
- Pipe roughness: The roughness of the pipe can create turbulence and affect the discharge.
- Pipe diameter: The diameter of the pipe can affect the discharge by changing the cross-sectional area of the flow.
- Fluid properties: The properties of the fluid, such as viscosity and density, can affect the discharge.
Applications of Discharge Formula
The discharge formula has a wide range of applications in various fields, including water supply systems, wastewater treatment, and flood control. It is used to design and operate pumps, turbines, and other fluid-handling equipment. Some key applications of the discharge formula are:
- Water supply systems: The discharge formula is used to design and operate water supply systems, including pipes and pumps.
- Wastewater treatment: The discharge formula is used to design and operate wastewater treatment plants, including pipes and treatment units.
- Flood control: The discharge formula is used to design and operate flood control systems, including levees and dams.
Limitations of Discharge Formula
The discharge formula has several limitations, including assumptions of steady-state flow and neglect of friction and other losses. It also assumes a simple geometry of the pipe or channel, which may not always be the case. Some key limitations of the discharge formula are:
- Assumptions: The discharge formula assumes a steady-state flow, which may not always be the case.
- Neglect of friction: The discharge formula neglects friction and other losses, which can affect the discharge.
- Simple geometry: The discharge formula assumes a simple geometry of the pipe or channel, which may not always be the case.
Measurement of Discharge
The discharge can be measured using various methods, including weirs, flumes, and meters. The choice of method depends on the accuracy required, the flow rate, and the fluid properties. Some key methods for measuring discharge are:
- Weirs: Weirs are used to measure discharge by creating a barrier to flow and measuring the head of water above the weir.
- Flumes: Flumes are used to measure discharge by creating a constricted section of the pipe or channel and measuring the head of water above the flume.
- Meters: Meters are used to measure discharge by measuring the flow rate directly, using a sensor or probe.
Frequently Asked Questions (FAQs)
What is the Discharge Time under Falling Head Formulae and Calculator?
The Discharge Time under Falling Head Formulae and Calculator is a mathematical tool used to calculate the time it takes for a certain volume of water to flow out of a reservoir or a tank under the influence of gravity. This formula is commonly used in hydrology and civil engineering to design and analyze water storage systems, such as dams and reservoirs. The formula takes into account the initial water level, final water level, and the cross-sectional area of the outlet, as well as the coefficient of discharge. By using this formula, engineers can determine the discharge time and flow rate of water from a reservoir, which is essential for designing and operating water supply systems. The Discharge Time under Falling Head Formulae and Calculator is a valuable tool for engineers and hydrologists, as it allows them to quickly and accurately calculate the discharge time and flow rate of water from a reservoir.
How does the Discharge Time under Falling Head Formulae and Calculator work?
The Discharge Time under Falling Head Formulae and Calculator works by using a mathematical formula that takes into account the physical properties of the reservoir and the outlet. The formula is based on the principle of conservation of mass, which states that the mass flow rate of water into the reservoir is equal to the mass flow rate of water out of the reservoir. The formula also takes into account the head loss that occurs as the water flows through the outlet, which is calculated using the Darcy-Weisbach equation. By inputting the initial water level, final water level, cross-sectional area of the outlet, and the coefficient of discharge, the calculator can determine the discharge time and flow rate of water from the reservoir. The calculator uses numerical methods to solve the equation and provide an accurate calculation of the discharge time and flow rate. The Discharge Time under Falling Head Formulae and Calculator is a powerful tool that can be used to design and analyze water storage systems, and it is widely used in hydrology and civil engineering.
What are the advantages of using the Discharge Time under Falling Head Formulae and Calculator?
The Discharge Time under Falling Head Formulae and Calculator has several advantages that make it a valuable tool for engineers and hydrologists. One of the main advantages is that it allows for quick and accurate calculations of the discharge time and flow rate of water from a reservoir. This is especially useful in emergency situations, such as flooding or drought, where fast and accurate calculations are crucial. Another advantage is that the calculator can be used to design and analyze water storage systems, such as dams and reservoirs. The calculator can also be used to optimize the design of water supply systems, by determining the optimal discharge time and flow rate of water from the reservoir. Additionally, the Discharge Time under Falling Head Formulae and Calculator is a cost-effective tool, as it eliminates the need for physical prototypes and experimental testing. Overall, the Discharge Time under Falling Head Formulae and Calculator is a powerful tool that can be used to improve the design and operation of water storage systems.
What are the limitations of the Discharge Time under Falling Head Formulae and Calculator?
The Discharge Time under Falling Head Formulae and Calculator has several limitations that need to be considered when using it. One of the main limitations is that the formula assumes a simple and idealized flow regime, which may not always be the case in real-world situations. The formula also assumes that the coefficient of discharge is constant, which may not be the case if the flow regime is complex or turbulent. Another limitation is that the calculator requires accurate input data, such as the initial water level, final water level, and cross-sectional area of the outlet. If the input data is inaccurate, the calculated discharge time and flow rate may also be inaccurate. Additionally, the Discharge Time under Falling Head Formulae and Calculator is a simplified tool that does not take into account other factors that may affect the flow regime, such as friction losses or energy losses. Therefore, the calculator should be used with caution and in conjunction with other design and analysis tools to ensure accurate and reliable results.
Deja una respuesta

Entradas Relacionadas