Section Modulus Equations and Calculators Common Shapes
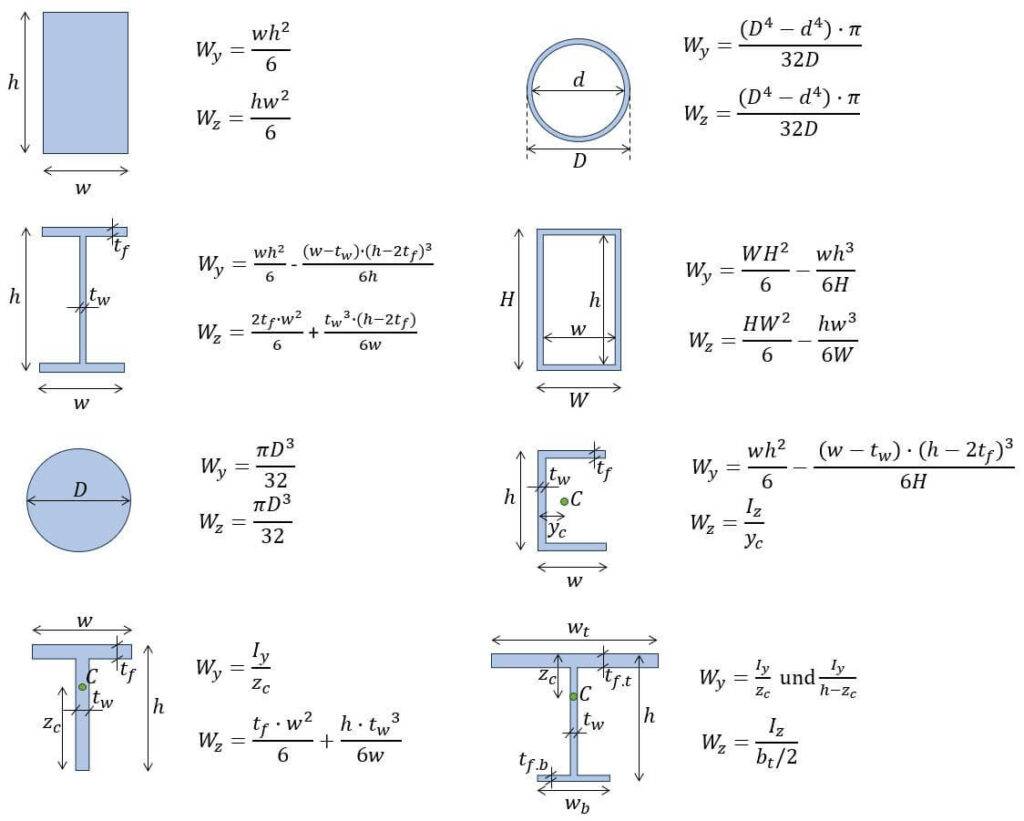
The section modulus is a crucial parameter in structural engineering, representing the ability of a cross-sectional shape to resist bending forces. Equations and calculators are essential tools for determining the section modulus of common shapes, such as beams, channels, and angles. These tools enable engineers to calculate the section modulus with precision, ensuring the structural integrity and safety of various constructions. This article provides an overview of section modulus equations and calculators for common shapes, facilitating accurate calculations and informed design decisions in engineering applications. Accurate calculations are vital for optimal design.
- Understanding Section Modulus Equations and Calculators for Common Shapes
- How do you calculate the section modulus?
- How do you find the section modulus of an irregular shape?
- What is the channel section modulus?
- What is the formula for the section modulus of a circular section?
- Frequently Asked Questions (FAQs)
Understanding Section Modulus Equations and Calculators for Common Shapes
The section modulus is a critical parameter in engineering and architecture, used to determine the bending and torsional strength of various shapes and structures. It is defined as the ratio of the moment of inertia to the distance from the neutral axis to the extreme fiber. In this context, calculators and equations play a vital role in simplifying the process of determining the section modulus for common shapes such as beams, columns, and other structural elements.
Beam Section Modulus Calculations
Calculating the section modulus for beams involves understanding the geometry of the beam and the materials used in its construction. The section modulus for a beam can be calculated using the formula: section modulus = moment of inertia / distance from neutral axis. This calculation is essential for determining the stress and strain on the beam under various loads.
Column Section Modulus Calculations
For columns, the section modulus calculation is similar to that of beams, but it also takes into account the axial load and buckling behavior. The section modulus for a column can be calculated using the formula: section modulus = moment of inertia / distance from neutral axis. This calculation is critical for determining the stability and strength of the column.
Section Modulus Equations for Common Shapes
The section modulus equations for common shapes such as rectangles, circles, and tubes can be derived using the moment of inertia and distance from neutral axis. For example, the section modulus for a rectangle can be calculated using the formula: section modulus = (base height^2) / 6. These equations are fundamental in engineering and architecture.
Calculators for Section Modulus
There are various calculators available that can simplify the process of calculating the section modulus for common shapes. These calculators can be online or offline and can be used to calculate the section modulus for beams, columns, and other structural elements. They are useful for engineers and architects who need to perform fast and accurate calculations.
Applications of Section Modulus in Engineering
The section modulus has numerous applications in engineering and architecture, including bridge design, building design, and machine design. It is used to determine the strength and stability of structures under various loads and to optimize the design of structures for maximum efficiency. The section modulus is also used in materials science to characterize the mechanical properties of materials.
| Shape | Section Modulus Formula | Moment of Inertia |
|---|---|---|
| Rectangle | (base height^2) / 6 | (base height^3) / 12 |
| Circle | (pi radius^3) / 4 | (pi radius^4) / 4 |
| Tube | (pi (outer radius^4 - inner radius^4)) / 4 | (pi (outer radius^4 - inner radius^4)) / 4 |
How do you calculate the section modulus?
To calculate the section modulus, you need to understand the geometry of the cross-section and the material properties. The section modulus is a measure of the flexural stiffness of a beam and is used to calculate the stress and deflection of a beam under load. It is defined as the ratio of the moment of inertia to the distance from the neutral axis to the extreme fiber. The formula for calculating the section modulus is: S = I / c, where S is the section modulus, I is the moment of inertia, and c is the distance from the neutral axis to the extreme fiber.
Understanding the Moment of Inertia
The moment of inertia is a critical parameter in calculating the section modulus. It is a measure of the resistance of a cross-section to bending and torsion. To calculate the moment of inertia, you need to know the shape and size of the cross-section. The formula for calculating the moment of inertia depends on the shape of the cross-section. For example:
- The moment of inertia for a rectangular cross-section is given by: I = (b h^3) / 12, where b is the width and h is the height.
- The moment of inertia for a circular cross-section is given by: I = (π d^4) / 64, where d is the diameter.
- The moment of inertia for an I-section is given by: I = (b h^3) / 12 - (b1 h1^3) / 12, where b1 and h1 are the width and height of the inner section.
Calculating the Distance from the Neutral Axis
The distance from the neutral axis to the extreme fiber is another important parameter in calculating the section modulus. The neutral axis is the line that passes through the centroid of the cross-section and is perpendicular to the axis of bending. The distance from the neutral axis to the extreme fiber can be calculated using the geometry of the cross-section. For example:
- The distance from the neutral axis to the extreme fiber for a rectangular cross-section is given by: c = h / 2, where h is the height.
- The distance from the neutral axis to the extreme fiber for a circular cross-section is given by: c = d / 2, where d is the diameter.
- The distance from the neutral axis to the extreme fiber for an I-section is given by: c = (h - h1) / 2, where h1 is the height of the inner section.
Applying the Section Modulus Formula
Once you have calculated the moment of inertia and the distance from the neutral axis to the extreme fiber, you can apply the section modulus formula. The formula is: S = I / c, where S is the section modulus, I is the moment of inertia, and c is the distance from the neutral axis to the extreme fiber. For example:
- For a rectangular cross-section with a width of 10 cm and a height of 20 cm, the moment of inertia is: I = (10 20^3) / 12 = 6667 cm^4, and the distance from the neutral axis to the extreme fiber is: c = 20 / 2 = 10 cm. The section modulus is: S = 6667 / 10 = 667 cm^3.
- For a circular cross-section with a diameter of 10 cm, the moment of inertia is: I = (π 10^4) / 64 = 490.1 cm^4, and the distance from the neutral axis to the extreme fiber is: c = 10 / 2 = 5 cm. The section modulus is: S = 490.1 / 5 = 98.02 cm^3.
- For an I-section with a width of 10 cm, a height of 20 cm, and an inner section width of 5 cm and height of 10 cm, the moment of inertia is: I = (10 20^3) / 12 - (5 10^3) / 12 = 5833 cm^4, and the distance from the neutral axis to the extreme fiber is: c = (20 - 10) / 2 = 5 cm. The section modulus is: S = 5833 / 5 = 1166.6 cm^3.
Considering the Material Properties
When calculating the section modulus, it is essential to consider the material properties, such as the density, elastic modulus, and yield strength. These properties can affect the behavior of the beam under load and the section modulus calculation. For example:
- The elastic modulus of the material can affect the stiffness of the beam and the section modulus calculation.
- The yield strength of the material can affect the maximum stress that the beam can withstand and the section modulus calculation.
- The density of the material can affect the weight of the beam and the section modulus calculation.
Calculating the Section Modulus for Complex Shapes
For complex shapes, such as channels, angles, and tubes, the calculation of the section modulus can be more complicated. In these cases, it is necessary to use numerical methods or approximations to calculate the moment of inertia and the distance from the neutral axis to the extreme fiber. For example:
- For a channel section, the moment of inertia can be calculated using the parallel axis theorem.
- For an angle section, the moment of inertia can be calculated using the perpendicular axis theorem.
- For a tube section, the moment of inertia can be calculated using the thin-walled approximation.
How do you find the section modulus of an irregular shape?

To find the section modulus of an irregular shape, you need to divide the shape into smaller, simpler shapes, and then calculate the section modulus for each part. The section modulus is a measure of the bending resistance of a shape, and it is calculated as the ratio of the moment of inertia to the distance from the neutral axis to the extreme fiber.
Understanding the Basics of Section Modulus
The section modulus is an important property of a shape, as it determines the shape's ability to resist bending stresses. To calculate the section modulus, you need to know the moment of inertia of the shape, which is a measure of the shape's resistance to bending. The moment of inertia can be calculated using the following formula: I = ∫(x^2)dA, where I is the moment of inertia, x is the distance from the neutral axis, and dA is the area of the infinitesimal element. Here are the steps to calculate the section modulus:
- Divide the shape into smaller, simpler shapes, such as rectangles or triangles.
- Calculate the moment of inertia for each part using the formula I = ∫(x^2)dA.
- Calculate the section modulus for each part using the formula Z = I/y, where Z is the section modulus, I is the moment of inertia, and y is the distance from the neutral axis to the extreme fiber.
Calculating the Moment of Inertia
The moment of inertia is a crucial property of a shape, and it is used to calculate the section modulus. The moment of inertia can be calculated using the following formula: I = ∫(x^2)dA, where I is the moment of inertia, x is the distance from the neutral axis, and dA is the area of the infinitesimal element. Here are the steps to calculate the moment of inertia:
- Choose a coordinate system and define the axes.
- Divide the shape into smaller, simpler shapes, such as rectangles or triangles.
- Calculate the moment of inertia for each part using the formula I = ∫(x^2)dA.
Dividing the Shape into Simpler Shapes
To calculate the section modulus of an irregular shape, you need to divide the shape into smaller, simpler shapes, such as rectangles or triangles. This is because the section modulus is a linear property, meaning that it can be calculated by summing the section moduli of the individual parts. Here are the steps to divide the shape into simpler shapes:
- Identify the boundaries of the shape and define the edges.
- Divide the shape into smaller, simpler shapes, such as rectangles or triangles.
- Calculate the area and perimeter of each part.
Using Numerical Methods to Calculate the Section Modulus
In some cases, it may be difficult or impossible to calculate the section modulus analytically, and numerical methods must be used. Finite element methods can be used to calculate the section modulus by discretizing the shape into smaller elements and solving the resulting system of equations. Here are the steps to use numerical methods:
- Choose a numerical method, such as the finite element method.
- Discretize the shape into smaller elements, such as triangles or quadrilaterals.
- Solve the resulting system of equations to calculate the section modulus.
Importance of Section Modulus in Engineering Design
The section modulus is a critical property of a shape, and it is used to determine the shape's ability to resist bending stresses. In engineering design, the section modulus is used to optimize the design of beams and columns, and to ensure that they can withstand the expected loads and stresses. Here are the steps to use the section modulus in engineering design:
- Calculate the maximum bending moment and shear force that the shape will experience.
- Calculate the required section modulus to resist the expected bending stresses.
- Use the section modulus to optimize the design of the shape, such as by minimizing the weight or cost.
What is the channel section modulus?
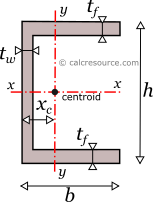
The channel section modulus refers to the geometric property of a channel section, which is a type of structural element used in construction and engineering. It is an important factor in determining the strength and stability of the channel section under various loads and stresses. The section modulus is calculated based on the cross-sectional area and the distance from the neutral axis to the extreme fiber of the section.
Definition and Formula
The section modulus is defined as the ratio of the moment of inertia of the section to the distance from the neutral axis to the extreme fiber. The formula for calculating the section modulus is: S = I / c, where S is the section modulus, I is the moment of inertia, and c is the distance from the neutral axis to the extreme fiber. The calculation of the section modulus involves the following steps:
- Calculate the moment of inertia of the section using the formula: I = (b h^3) / 12, where b is the width and h is the height of the section.
- Determine the distance from the neutral axis to the extreme fiber, which is typically half the height of the section.
- Use the formula S = I / c to calculate the section modulus.
Importance in Structural Design
The channel section modulus plays a crucial role in structural design, as it helps engineers determine the load-carrying capacity of the channel section. A higher section modulus indicates a stronger and more stable section, which can support greater loads and stresses. The section modulus is also used to calculate the section properties, such as the section area and moment of inertia, which are essential for analyzing the structural behavior of the channel section. The importance of the section modulus in structural design can be seen in the following aspects:
- Load calculation: The section modulus is used to calculate the maximum load that the channel section can support.
- Stress analysis: The section modulus helps engineers analyze the stresses and strains in the channel section under various loads.
- Material selection: The section modulus is used to select the appropriate material for the channel section based on its strength and stability requirements.
Factors Affecting Section Modulus
The channel section modulus is affected by several geometric factors, including the width, height, and thickness of the section. The material properties, such as the density and elastic modulus, also influence the section modulus. Additionally, the loading conditions, including the type and magnitude of the loads, can impact the section modulus. The factors affecting the section modulus can be summarized as follows:
- Geometric factors: The width, height, and thickness of the section affect the section modulus.
- Material properties: The density and elastic modulus of the material influence the section modulus.
- Loading conditions: The type and magnitude of the loads affect the section modulus.
Applications in Construction
The channel section modulus has numerous practical applications in construction, including the design of beams, columns, and frames. It is used to determine the size and shape of the channel section required to support specific loads and stresses. The section modulus is also used in the design of structural connections, such as welds and bolts, to ensure that they can transmit the required forces and moments. The applications of the section modulus in construction can be seen in the following areas:
- Building design: The section modulus is used to design beams and columns that can support the weight of the building.
- Bridge design: The section modulus is used to design bridge girders and piers that can support the weight of the bridge and the traffic loads.
- Industrial structures: The section modulus is used to design industrial structures, such as cranes and conveyors, that require high strength and stability.
Conclusion and Future Directions
The channel section modulus is a critical geometric property that plays a vital role in structural design and construction. Its calculation and application are essential for ensuring the safety and stability of structures under various loads and stresses. As building codes and design standards continue to evolve, the importance of the section modulus will only continue to grow. The future directions for the section modulus include the development of new materials and design methods that can optimize the section modulus for improved performance and efficiency. The future directions for the section modulus can be summarized as follows:
- New materials: The development of new materials with high strength and stability will require the calculation of the section modulus to ensure their safe and efficient use.
- Design methods: The development of new design methods and software will enable the calculation of the section modulus with greater accuracy and speed.
- Optimization techniques: The development of optimization techniques will enable the optimization of the section modulus for improved performance and efficiency.
What is the formula for the section modulus of a circular section?

The formula for the section modulus of a circular section is given by the equation: Z = (π d^3) / 32, where Z is the section modulus, π (pi) is a mathematical constant approximately equal to 3.14159, and d is the diameter of the circular section.
Understanding Section Modulus
The section modulus is a structural engineering concept used to calculate the bending stress of a beam. It is an important factor in determining the strength and stability of a beam under load. To understand the section modulus, it is essential to know the geometry of the beam and the type of load it will be subjected to.
- The section modulus is used to calculate the bending moment of a beam.
- It is an important factor in determining the deflection of a beam under load.
- The section modulus is used in conjunction with the moment of inertia to calculate the stress in a beam.
Calculating Section Modulus
Calculating the section modulus of a circular section involves using the formula Z = (π d^3) / 32. This requires knowing the diameter of the circular section.
- The diameter of the circular section must be known to calculate the section modulus.
- The formula for the section modulus of a circular section is a simplified version of the more general formula for the section modulus of a beam.
- The section modulus is used to calculate the allowable stress of a beam under load.
Importance of Section Modulus
The section modulus is a critical factor in structural engineering as it helps to determine the strength and stability of a beam under load. A higher section modulus indicates a stronger beam that can withstand greater bending forces.
- A higher section modulus indicates a stronger beam.
- The section modulus is used to calculate the deflection of a beam under load.
- The section modulus is an important factor in determining the type of material to use for a beam.
Section Modulus and Beam Design
The section modulus plays a crucial role in beam design as it helps to determine the size and shape of the beam. By using the section modulus formula, engineers can design beams that can withstand the expected loads and stresses.
- The section modulus is used to determine the size of a beam.
- The section modulus is used to determine the shape of a beam.
- The section modulus is used in conjunction with the moment of inertia to design beams.
Applications of Section Modulus
The section modulus has a wide range of applications in structural engineering, including the design of beams, columns, and bridges. It is also used in the analysis of existing structures to determine their strength and stability.
- The section modulus is used in the design of beams and columns.
- The section modulus is used in the analysis of existing structures.
- The section modulus is used in the design of bridges and other complex structures.
Frequently Asked Questions (FAQs)
What is the Section Modulus and its Importance in Engineering?
The Section Modulus is a fundamental concept in engineering, particularly in the field of mechanics of materials. It is a measure of the flexural rigidity of a beam, which is essential in determining the beam's ability to resist bending stresses. The section modulus is calculated using the moment of inertia of the beam's cross-sectional area and is typically denoted by the symbol S. A higher section modulus indicates a greater resistance to bending, making it a critical factor in the design of beams and other structural elements. In engineering applications, the section modulus is used to calculate the maximum bending stress that a beam can withstand, ensuring that the beam does not fail under external loads.
How are Section Modulus Equations Used in Calculating Common Shapes?
Section modulus equations are used to calculate the section modulus of various common shapes, such as rectangular beams, circular beams, and I-beams. These equations take into account the geometric properties of the shape, such as the width, height, and radius, to determine the section modulus. For example, the section modulus of a rectangular beam is calculated using the equation S = (1/6) b h^2, where b is the width and h is the height of the beam. Similarly, the section modulus of a circular beam is calculated using the equation S = (π d^3) / 32, where d is the diameter of the beam. These equations are essential in calculating the section modulus of different shapes, allowing engineers to determine the structural integrity of the beam.
What are the Different Types of Section Modulus Calculators Available?
There are several types of section modulus calculators available, each with its own unique features and capabilities. Online calculators are a popular choice, as they are easily accessible and can perform calculations quickly and accurately. These calculators often have a user-friendly interface that allows users to input the geometric properties of the shape and calculate the section modulus instantly. Software-based calculators are another type of calculator that can be used to calculate the section modulus. These calculators are often more advanced and can perform complex calculations, such as finite element analysis, to determine the section modulus. Additionally, mobile apps are also available, allowing users to calculate the section modulus on-the-go.
How do Engineers Apply Section Modulus Equations and Calculators in Real-World Applications?
Engineers apply section modulus equations and calculators in a variety of real-world applications, including the design of bridges, buildings, and machinery. By calculating the section modulus, engineers can determine the structural integrity of a beam or other structural element, ensuring that it can withstand external loads and stresses. For example, in the design of a bridge, engineers use section modulus equations to calculate the section modulus of the bridge's beams, ensuring that they can withstand the weight of traffic and environmental stresses. Similarly, in the design of a building, engineers use section modulus calculators to determine the section modulus of the building's columns and beams, ensuring that they can withstand wind loads and seismic activity. By applying section modulus equations and calculators, engineers can ensure that their designs are safe, efficient, and cost-effective.
Deja una respuesta

Entradas Relacionadas