Isentropic Flow of Fluid Equations and Calculator
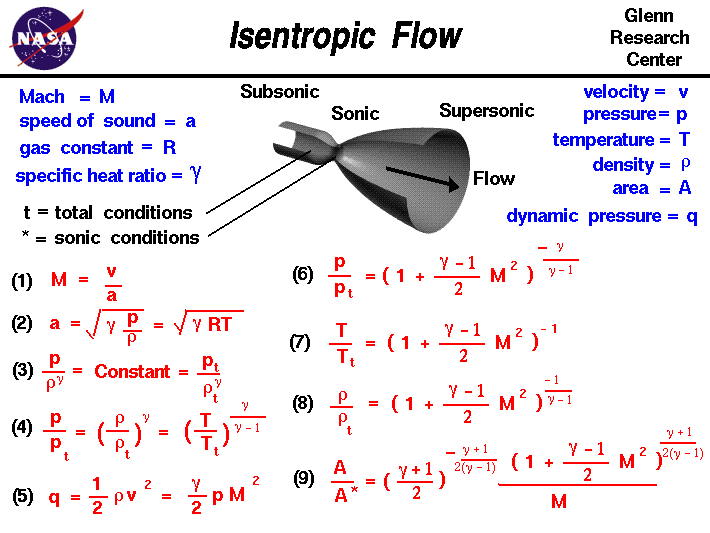
The isentropic flow of fluids is a crucial concept in thermodynamics and fluid dynamics. It describes the flow of a fluid in which the entropy remains constant, resulting in a process that is both adiabatic and reversible. The equations governing isentropic flow are fundamental in designing and optimizing various engineering systems, such as nozzles, turbines, and compressors. This article provides an overview of the key equations and a calculator for isentropic flow, enabling engineers to accurately predict and analyze the behavior of fluids in these systems, ensuring efficient and reliable performance.
- Understanding Isentropic Flow of Fluid Equations and Calculator
- What is the equation for the isentropic process?
- How to determine if flow is isentropic?
- What is the Bernoulli equation for isentropic flow?
- How do you calculate dynamic pressure from Mach number?
-
Frequently Asked Questions (FAQs)
- What is Isentropic Flow and How Does it Relate to Fluid Equations?
- How Do I Use the Isentropic Flow Calculator to Solve Fluid Flow Problems?
- What are the Key Assumptions and Limitations of the Isentropic Flow Equations?
- How Can I Apply the Isentropic Flow Equations to Real-World Fluid Flow Problems?
Understanding Isentropic Flow of Fluid Equations and Calculator
The isentropic flow of fluids is a fundamental concept in fluid dynamics, which describes the behavior of fluids when they undergo a process without any heat transfer or friction. This type of flow is idealized, as it assumes that the fluid is inviscid and that there are no dissipative forces acting on it. The isentropic flow equations are a set of mathematical equations that govern this type of flow, and they are widely used in various fields, including aerospace engineering, chemical engineering, and mechanical engineering.
Introduction to Isentropic Flow Equations
The isentropic flow equations are derived from the conservation laws of mass, momentum, and energy. These equations describe the relationship between the pressure, density, velocity, and temperature of a fluid in motion. The isentropic flow is characterized by the fact that the entropy of the fluid remains constant throughout the flow. This means that the fluid undergoes a reversible process, where the entropy change is zero.
Isentropic Flow Calculator
An isentropic flow calculator is a tool that is used to calculate the properties of a fluid in isentropic flow. This calculator can be used to determine the pressure, density, velocity, and temperature of a fluid at different points in the flow. The calculator uses the isentropic flow equations to calculate these properties, and it can be used to analyze various types of fluid flow problems, including nozzles, diffusers, and ducts.
Assumptions and Limitations of Isentropic Flow
The isentropic flow assumes that the fluid is inviscid and that there are no dissipative forces acting on it. This means that the fluid has no viscosity and that there are no frictional forces or heat transfer occurring in the flow. These assumptions are not always valid, and the isentropic flow equations may not accurately predict the behavior of real fluids. However, the isentropic flow can be used as a theoretical model to understand the behavior of fluids in various types of flow problems.
Applications of Isentropic Flow Equations
The isentropic flow equations have various applications in different fields, including aerospace engineering, chemical engineering, and mechanical engineering. These equations can be used to analyze the performance of nozzles, diffusers, and ducts, and to design more efficient systems. The isentropic flow can also be used to understand the behavior of compressible fluids, such as gases, and to analyze the effects of friction and heat transfer on fluid flow.
Key Parameters in Isentropic Flow
The key parameters in isentropic flow include the pressure, density, velocity, and temperature of the fluid. These parameters are related to each other through the isentropic flow equations, and they can be used to calculate the properties of the fluid at different points in the flow. The following table shows the key parameters in isentropic flow:
| Parameter | Symbol | Unit |
|---|---|---|
| Pressure | P | Pascal (Pa) |
| Density | ρ | Kilogram per cubic meter (kg/m³) |
| Velocity | u | Meter per second (m/s) |
| Temperature | T | Kelvin (K) |
What is the equation for the isentropic process?

The equation for the isentropic process is given by the formula: PV^γ = constant, where P is the pressure, V is the volume, and γ is the adiabatic index. This equation describes the relationship between the pressure and volume of a system during an isentropic process, which is a thermodynamic process that occurs without any heat transfer.
Derivation of the Isentropic Process Equation
The equation for the isentropic process can be derived from the first law of thermodynamics and the ideal gas law. The derivation involves assuming that the process is reversible and that there is no heat transfer. The resulting equation is a mathematical representation of the relationship between the pressure and volume of a system during an isentropic process. Some key points to consider when deriving this equation include:
- The ideal gas law, which states that PV = nRT, where n is the number of moles and R is the gas constant.
- The first law of thermodynamics, which states that ΔE = Q - W, where ΔE is the change in energy, Q is the heat transfer, and W is the work done.
- The adiabatic index, which is a measure of the ratio of specific heats and is denoted by the symbol γ.
Applications of the Isentropic Process Equation
The equation for the isentropic process has a wide range of applications in engineering and physics. It can be used to analyze the behavior of gases and fluids in various systems, including engines, pumps, and turbines. Some key applications of this equation include:
- Design of engines, where the isentropic process equation is used to optimize the efficiency and performance of the engine.
- Analysis of fluid flow, where the equation is used to study the behavior of fluids in pipes and channels.
- Optimization of thermodynamic systems, where the equation is used to minimize energy losses and maximize efficiency.
Assumptions of the Isentropic Process Equation
The equation for the isentropic process is based on several assumptions, including the assumption that the process is reversible and that there is no heat transfer. Other assumptions include:
- The system is closed, meaning that there is no mass transfer across the boundary.
- The process is adiabatic, meaning that there is no heat transfer between the system and the surroundings.
- The fluid is ideal, meaning that it obeys the ideal gas law.
Limits of the Isentropic Process Equation
The equation for the isentropic process has several limits and limitations, including the assumption that the process is reversible and that there is no heat transfer. Other limitations include:
- The equation is only applicable to ideal gases, and does not account for real gas behavior.
- The equation assumes that the process is slow and quasi-static, meaning that the system is always in equilibrium.
- The equation does not account for friction or dissipation, which can occur in real systems.
Comparison with Other Thermodynamic Processes
The isentropic process equation can be compared to other thermodynamic processes, including the isothermal and adiabatic processes. Some key differences between these processes include:
- The isothermal process, which occurs at constant temperature, and is described by the equation PV = constant.
- The adiabatic process, which occurs without heat transfer, and is described by the equation PV^γ = constant.
- The polytropic process, which is a more general process that can be used to describe a wide range of thermodynamic processes.
How to determine if flow is isentropic?
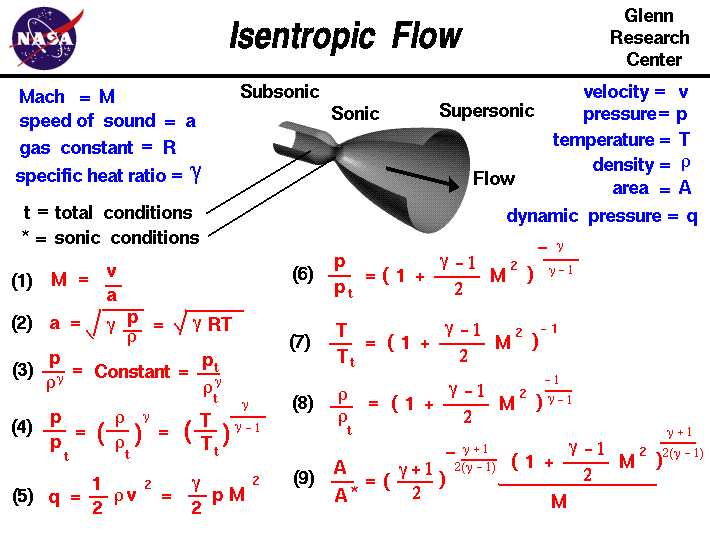
To determine if a flow is isentropic, it is essential to understand the concept of entropy and its relationship with the flow. Isentropic flow refers to a flow where the entropy remains constant throughout the system. This can be achieved when there is no heat transfer or friction in the system, and the flow is reversible. In practice, it is challenging to achieve a perfectly isentropic flow, but it can be approximated by minimizing irreversibilities.
Conditions for Isentropic Flow
To determine if a flow is isentropic, the following conditions must be met:
- The flow must be adiabatic, meaning there is no heat transfer between the system and its surroundings.
- The flow must be frictionless, meaning there are no viscous forces or turbulence that can cause energy losses.
- The flow must be reversible, meaning that it can be reversed without any energy losses or entropy generation.
These conditions are ideal and can be difficult to achieve in practice. However, by understanding these conditions, engineers can design systems that approximate isentropic flow, minimizing irreversibilities and maximizing efficiency.
Importance of Isentropic Flow
Isentropic flow is crucial in various engineering applications, including aerodynamics, gas turbines, and compressors. In these applications, isentropic efficiency is used to evaluate the performance of the system. Isentropic flow allows for the calculation of ideal performance, which can be used as a benchmark to compare actual performance.
- Isentropic efficiency is a measure of how close the actual performance is to the ideal performance.
- Isentropic flow is used to calculate the ideal work output or ideal work input of a system.
- Isentropic flow is essential in designing high-efficiency systems, such as gas turbines and compressors.
By understanding isentropic flow, engineers can optimize system design and improve overall performance.
Calculating Isentropic Flow
Calculating isentropic flow involves using thermodynamic equations and conservation laws. The isentropic process can be modeled using the ideal gas equation, which relates pressure, temperature, and density.
- The isentropic exponent is used to calculate the pressure and temperature relationship during an isentropic process.
- Isentropic tables or charts can be used to calculate isentropic flow properties, such as temperature, pressure, and density.
- Computational fluid dynamics can be used to simulate isentropic flow and calculate flow properties.
These calculations are essential in designing and analyzing isentropic flow systems.
Assumptions and Limitations
When determining if a flow is isentropic, several assumptions and limitations must be considered.
- The ideal gas assumption is often used to simplify isentropic flow calculations.
- Friction and heat transfer must be minimized to approximate isentropic flow.
- Turbulence and viscous forces can cause irreversibilities and affect isentropic flow.
Understanding these assumptions and limitations is crucial in designing and analyzing isentropic flow systems.
Real-World Applications
Isentropic flow has numerous real-world applications, including aerospace engineering, power generation, and chemical processing.
- Gas turbines and jet engines rely on isentropic flow to achieve high efficiency and performance.
- Compressors and pumps use isentropic flow to calculate ideal work input and efficiency.
- Wind turbines and hydroelectric turbines can be designed using isentropic flow principles to optimize energy production.
These applications demonstrate the importance of isentropic flow in real-world engineering design and analysis.
What is the Bernoulli equation for isentropic flow?

The Bernoulli equation for isentropic flow is a fundamental concept in fluid dynamics that describes the relationship between the pressure, density, and velocity of a fluid in motion. The equation is derived from the conservation of energy principle and is commonly used to analyze the behavior of fluids in various engineering applications. The Bernoulli equation for isentropic flow is given by the equation: P/ρ + 1/2 v^2 + gz = constant, where P is the pressure, ρ is the density, v is the velocity, g is the acceleration due to gravity, and z is the height.
Derivation of the Bernoulli Equation
The derivation of the Bernoulli equation for isentropic flow involves the application of the conservation of energy principle to a fluid element. The equation is derived by considering the work done on the fluid element by the surrounding fluid and the change in energy of the fluid element. The resulting equation is a statement of the conservation of energy principle, which can be written in terms of the pressure, density, and velocity of the fluid. Some key points to consider when deriving the Bernoulli equation include:
- The conservation of mass principle must be satisfied, which means that the mass flow rate into and out of the fluid element must be equal.
- The conservation of energy principle must be satisfied, which means that the energy entering and leaving the fluid element must be equal.
- The fluid properties, such as pressure, density, and velocity, must be defined at each point in the flow field.
Assumptions of the Bernoulli Equation
The Bernoulli equation for isentropic flow is based on several assumptions, including the assumption of steady flow, incompressible flow, and irrotational flow. The equation also assumes that the fluid is inviscid, meaning that it has no viscosity. These assumptions simplify the equation and make it easier to apply to a wide range of engineering problems. Some key assumptions to consider when applying the Bernoulli equation include:
- The flow must be steady, meaning that the velocity and pressure at each point in the flow field must be constant with time.
- The flow must be incompressible, meaning that the density of the fluid must be constant throughout the flow field.
- The flow must be irrotational, meaning that the vorticity of the fluid must be zero.
Applications of the Bernoulli Equation
The Bernoulli equation for isentropic flow has a wide range of applications in engineering, including the design of aircraft, wind turbines, and hydroelectric power plants. The equation is also used to analyze the behavior of fluids in pipes and channels, and to predict the pressure and velocity of fluids in various engineering systems. Some key applications to consider when using the Bernoulli equation include:
- The design of aircraft, where the Bernoulli equation is used to predict the lift and drag forces on the wings and fuselage.
- The design of wind turbines, where the Bernoulli equation is used to predict the power output of the turbine.
- The design of hydroelectric power plants, where the Bernoulli equation is used to predict the power output of the turbine.
Limitations of the Bernoulli Equation
The Bernoulli equation for isentropic flow has several limitations, including the assumption of inviscid flow, which can lead to inaccurate predictions of the flow field. The equation also assumes that the flow is steady and incompressible, which can limit its application to certain types of fluids and flow regimes. Some key limitations to consider when using the Bernoulli equation include:
- The equation assumes inviscid flow, which can lead to inaccurate predictions of the flow field.
- The equation assumes steady flow, which can limit its application to certain types of fluids and flow regimes.
- The equation assumes incompressible flow, which can limit its application to certain types of fluids and flow regimes.
Numerical Methods for Solving the Bernoulli Equation
The Bernoulli equation for isentropic flow can be solved numerically using a variety of methods, including the finite difference method and the finite element method. These methods involve discretizing the flow field into a set of grid points and solving the resulting system of algebraic equations. Some key numerical methods to consider when solving the Bernoulli equation include:
- The finite difference method, which involves discretizing the flow field into a set of grid points and solving the resulting system of algebraic equations.
- The finite element method, which involves discretizing the flow field into a set of elements and solving the resulting system of algebraic equations.
- The boundary element method, which involves discretizing the boundary of the flow field into a set of elements and solving the resulting system of algebraic equations.
How do you calculate dynamic pressure from Mach number?
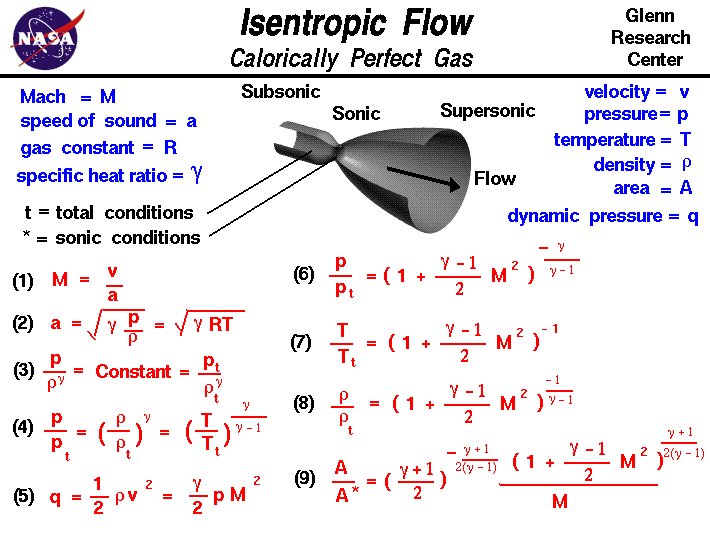
To calculate dynamic pressure from Mach number, you need to use the formula: q = 0.5 ρ v^2, where q is the dynamic pressure, ρ is the air density, and v is the velocity of the object. However, since you are given the Mach number, you can use the formula: M = v / a, where M is the Mach number, v is the velocity, and a is the speed of sound. By rearranging this formula, you can solve for velocity: v = M a. Then, you can plug this expression for velocity into the dynamic pressure formula: q = 0.5 ρ (M a)^2.
Understanding the Concept of Dynamic Pressure
Dynamic pressure is a measure of the kinetic energy of a fluid, such as air, as it moves around an object. To calculate dynamic pressure, you need to know the density of the fluid and the velocity of the object. The formula for dynamic pressure is q = 0.5 ρ v^2, where q is the dynamic pressure, ρ is the air density, and v is the velocity of the object. Here are the steps to calculate dynamic pressure:
- Calculate the velocity of the object using the Mach number formula: v = M a
- Calculate the air density using the formula: ρ = P / (R T), where P is the pressure, R is the gas constant, and T is the temperature
- Plug the values of velocity and air density into the dynamic pressure formula: q = 0.5 ρ v^2
Relating Mach Number to Dynamic Pressure
The Mach number is a dimensionless quantity that represents the ratio of an object's velocity to the speed of sound. To relate Mach number to dynamic pressure, you need to use the formula: M = v / a, where M is the Mach number, v is the velocity, and a is the speed of sound. By rearranging this formula, you can solve for velocity: v = M a. Then, you can plug this expression for velocity into the dynamic pressure formula: q = 0.5 ρ (M a)^2. Here are the steps to relate Mach number to dynamic pressure:
- Calculate the velocity of the object using the Mach number formula: v = M a
- Calculate the speed of sound using the formula: a = √(γ R T), where γ is the adiabatic index, R is the gas constant, and T is the temperature
- Plug the values of velocity and speed of sound into the dynamic pressure formula: q = 0.5 ρ (M a)^2
Importance of Air Density in Dynamic Pressure Calculation
Air density plays a crucial role in the calculation of dynamic pressure. The formula for dynamic pressure is q = 0.5 ρ v^2, where q is the dynamic pressure, ρ is the air density, and v is the velocity of the object. To calculate air density, you need to know the pressure and temperature of the air. The formula for air density is ρ = P / (R T), where P is the pressure, R is the gas constant, and T is the temperature. Here are the steps to calculate air density:
- Measure the pressure and temperature of the air
- Calculate the gas constant using the formula: R = R_universal / M_molecular, where R_universal is the universal gas constant and M_molecular is the molecular weight of the gas
- Plug the values of pressure, temperature, and gas constant into the air density formula: ρ = P / (R T)
Role of Velocity in Dynamic Pressure Calculation
Velocity is a critical component in the calculation of dynamic pressure. The formula for dynamic pressure is q = 0.5 ρ v^2, where q is the dynamic pressure, ρ is the air density, and v is the velocity of the object. To calculate velocity, you need to know the Mach number and the speed of sound. The formula for velocity is v = M a, where M is the Mach number and a is the speed of sound. Here are the steps to calculate velocity:
- Calculate the Mach number using the formula: M = v / a
- Calculate the speed of sound using the formula: a = √(γ R T), where γ is the adiabatic index, R is the gas constant, and T is the temperature
- Plug the values of Mach number and speed of sound into the velocity formula: v = M a
Applications of Dynamic Pressure Calculation
The calculation of dynamic pressure has numerous applications in various fields, including aerospace engineering, automotive engineering, and wind engineering. Dynamic pressure is used to calculate the lift and drag forces on an object, as well as the thrust and torque of an engine. Here are some examples of applications:
- Aircraft design: Dynamic pressure is used to calculate the lift and drag forces on an aircraft, which is essential for determining its performance and stability
- Automotive engineering: Dynamic pressure is used to calculate the drag force on a vehicle, which is important for determining its fuel efficiency and performance
- Wind engineering: Dynamic pressure is used to calculate the wind loads on buildings and bridges, which is essential for determining their structural integrity
Frequently Asked Questions (FAQs)
What is Isentropic Flow and How Does it Relate to Fluid Equations?
Isentropic flow refers to the flow of fluids in which the entropy remains constant. This type of flow is idealized and assumes that there are no irreversible processes, such as friction or heat transfer, occurring within the fluid. In reality, isentropic flow is not achievable, but it serves as a useful theoretical model for understanding the behavior of fluids under various conditions. The equations of motion for isentropic flow can be derived from the conservation laws of mass, momentum, and energy, and are commonly used in the design and analysis of nozzles, diffusers, and other fluid flow devices. By assuming isentropic flow, engineers can predict the pressure, temperature, and velocity of a fluid as it flows through a system, and optimize the design to achieve maximum efficiency.
How Do I Use the Isentropic Flow Calculator to Solve Fluid Flow Problems?
The isentropic flow calculator is a powerful tool for solving fluid flow problems. To use the calculator, simply input the known parameters of the problem, such as the upstream pressure and temperature, and the downstream pressure or Mach number. The calculator will then use the isentropic flow equations to calculate the unknown quantities, such as the downstream temperature, velocity, and density. The calculator can also be used to iterate on the design of a fluid flow system, allowing engineers to quickly and easily optimize the performance of the system. By using the calculator, engineers can save time and effort compared to solving the equations manually, and can focus on higher-level design decisions. The calculator is also user-friendly, with a simple and intuitive interface that makes it easy to input data and interpret the results.
What are the Key Assumptions and Limitations of the Isentropic Flow Equations?
The isentropic flow equations are based on several key assumptions, including that the flow is one-dimensional, steady, and inviscid. The equations also assume that the fluid is perfectly gas, with constant specific heats, and that there are no heat transfer or friction losses. In reality, these assumptions are not always valid, and the actual flow may be two-dimensional or unsteady, with viscous effects and heat transfer playing an important role. Additionally, the equations are limited to subsonic and supersonic flows, and do not account for transonic or hypersonic flows. Despite these limitations, the isentropic flow equations remain a valuable tool for engineers, providing a simple and accurate way to model and analyze fluid flow problems. By understanding the assumptions and limitations of the equations, engineers can use them effectively and confidently.
How Can I Apply the Isentropic Flow Equations to Real-World Fluid Flow Problems?
The isentropic flow equations have a wide range of practical applications in fields such as aerospace engineering, chemical engineering, and mechanical engineering. For example, the equations can be used to design and analyze nozzle and diffuser systems, turbomachinery, and wind tunnels. The equations can also be used to model and simulate complex fluid flow phenomena, such as shock waves and boundary layers. By applying the isentropic flow equations, engineers can optimize the performance of fluid flow systems, reduce energy losses, and improve efficiency. The equations can also be used to validate and calibrate experimental data, and to inform and guide the design of new fluid flow systems. By understanding the underlying physics of the isentropic flow equations, engineers can apply them effectively and creatively to a wide range of real-world problems.
Deja una respuesta

Entradas Relacionadas