Compression Buckling in Unstiffened Plates Formula and Calculator
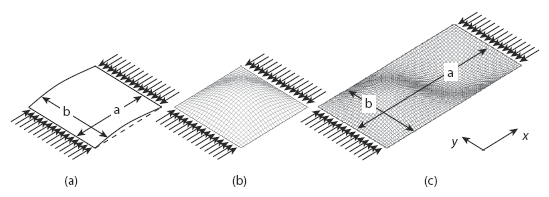
Compression buckling in unstiffened plates is a critical phenomenon that occurs when a plate is subjected to compressive loads, causing it to buckle or deform. This behavior is a major concern in various engineering applications, including aerospace, civil, and mechanical engineering. The buckling load capacity of a plate is a crucial factor in determining its structural integrity. This article provides an overview of the formula and calculator used to determine the compression buckling load of unstiffened plates, highlighting the key parameters and equations involved in the calculation process to ensure accurate predictions and designs.
- Compression Buckling in Unstiffened Plates: Understanding the Formula and Calculator
- What is the formula for the buckling load factor?
- What is the formula for the buckling of a cylinder?
- What is Euler's formula for buckling?
- What is the formula for allowable buckling stress?
-
Frequently Asked Questions (FAQs)
- What is Compression Buckling in Unstiffened Plates and How is it Calculated?
- How Does the Formula for Compression Buckling in Unstiffened Plates Account for Different Material Properties?
- What are the Limitations of the Formula for Compression Buckling in Unstiffened Plates, and How Can They be Addressed?
- How Can the Calculator for Compression Buckling in Unstiffened Plates be Used in Practice, and What are the Benefits of Using it?
Compression Buckling in Unstiffened Plates: Understanding the Formula and Calculator
Compression buckling in unstiffened plates is a critical phenomenon that occurs when a plate is subjected to compressive loads, leading to a loss of stability and potentially catastrophic failure. The compressive stress and buckling load are crucial factors in determining the plate's behavior. To accurately predict the onset of buckling, engineers use a combination of mathematical formulas and calculators.
Introduction to Compression Buckling in Unstiffened Plates
Compression buckling in unstiffened plates is a complex problem that involves the interaction of several factors, including the plate's geometric properties, such as its length, width, and thickness, as well as the material properties, like the modulus of elasticity and Poisson's ratio. The critical buckling stress is the maximum stress that the plate can withstand without buckling, and it is typically calculated using the Euler formula.
Formula for Compression Buckling in Unstiffened Plates
The formula for compression buckling in unstiffened plates is given by the Euler equation: σ_cr = (π^2 E) / (12 (1 - ν^2)) (t / b)^2, where σ_cr is the critical buckling stress, E is the modulus of elasticity, ν is Poisson's ratio, t is the plate thickness, and b is the plate width. This formula provides a theoretical prediction of the critical buckling stress, which can be used to design and optimize unstiffened plates.
Calculator for Compression Buckling in Unstiffened Plates
A calculator for compression buckling in unstiffened plates can be a valuable tool for engineers, allowing them to quickly and accurately determine the critical buckling load and stress. These calculators typically use the Euler formula as a basis and can be programmed to include additional factors, such as boundary conditions and material nonlinearity. By using a calculator, engineers can save time and reduce the risk of errors in their calculations.
Factors Influencing Compression Buckling in Unstiffened Plates
Several factors can influence the compression buckling behavior of unstiffened plates, including the plate's aspect ratio, material properties, and boundary conditions. The aspect ratio, which is the ratio of the plate's length to its width, can significantly affect the critical buckling stress. Additionally, the material properties, such as the yield strength and ultimate tensile strength, can impact the plate's ability to withstand compressive loads.
Applications of Compression Buckling in Unstiffened Plates
Compression buckling in unstiffened plates has numerous applications in various fields, including aerospace engineering, civil engineering, and mechanical engineering. In aerospace engineering, for example, unstiffened plates are often used in the design of aircraft wings and fuselages, where the compressive loads can be significant. By understanding and predicting the compression buckling behavior of these plates, engineers can design safer and more efficient structures.
| Parameter | Description |
|---|---|
| Critical Buckling Stress | The maximum stress that the plate can withstand without buckling |
| Modulus of Elasticity | A measure of the plate's stiffness and ability to withstand compressive loads |
| Poisson's Ratio | A measure of the plate's lateral strain response to axial loading |
| Plate Thickness | The distance between the plate's top and bottom surfaces |
| Plate Width | The distance between the plate's left and right edges |
What is the formula for the buckling load factor?
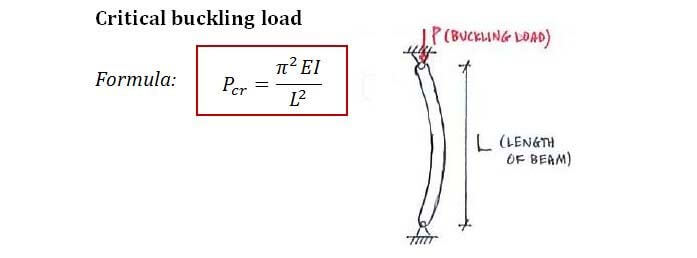
The formula for the buckling load factor is given by the Euler's critical load formula, which is a fundamental concept in structural engineering. The buckling load factor is a measure of the load that a column can withstand before it buckles or collapses. The formula is: P = (π^2 E I) / (K L^2), where P is the critical load, E is the modulus of elasticity, I is the moment of inertia, K is the end condition factor, and L is the length of the column.
Derivation of the Buckling Load Factor Formula
The derivation of the buckling load factor formula involves the use of differential equations to model the behavior of a column under load. The formula is derived by assuming that the column is a slender beam and that the load is applied at the top of the column. The boundary conditions are also taken into account, including the end conditions of the column. Some key points to consider when deriving the formula are:
- The assumptions made about the column, such as its slenderness ratio and end conditions
- The mathematical models used to describe the behavior of the column, such as the Euler-Bernoulli beam theory
- The simplifications made to the model, such as neglecting shear deformations and rotary inertia
Factors Affecting the Buckling Load Factor
The buckling load factor is affected by several factors, including the material properties of the column, such as its elastic modulus and yield strength. The geometric properties of the column, such as its length, diameter, and wall thickness, also play a crucial role. Other factors that can affect the buckling load factor include:
- The end conditions of the column, such as pinned or fixed ends
- The Loading conditions, such as axial load or bending moment
- The imperfections in the column, such as initial curvature or eccentricity
Applications of the Buckling Load Factor Formula
The buckling load factor formula has numerous applications in engineering design, particularly in the design of columns, beams, and frames. The formula is used to determine the maximum load that a structure can withstand before it buckles or collapses. Some key applications of the formula include:
- Structural analysis and design of buildings, bridges, and other infrastructure
- Mechanical engineering design of machines and mechanisms
- Aerospace engineering design of aircraft and spacecraft
Limitations of the Buckling Load Factor Formula
The buckling load factor formula has several limitations, including its assumption of a perfect column with no imperfections. The formula also neglects the effects of shear deformations and rotary inertia, which can be significant in thick-walled columns. Other limitations of the formula include:
- The simplifications made to the model, such as neglecting non-linear effects
- The assumptions made about the material properties, such as isotropy and homogeneity
- The lack of consideration for dynamic loads and time-dependent effects
Extensions and Modifications of the Buckling Load Factor Formula
The buckling load factor formula has been extended and modified to account for various effects, such as non-linear material behavior and imperfections. Some key extensions and modifications of the formula include:
- The inclusion of shear deformations and rotary inertia in the model
- The consideration of non-linear effects, such as large deflections and material non-linearity
- The development of new formulas for specific applications, such as composite columns and functionally graded materials
What is the formula for the buckling of a cylinder?

The formula for the buckling of a cylinder is a complex equation that takes into account the cylinder's geometry, material properties, and loading conditions. The critical load at which the cylinder buckles can be calculated using the Euler formula, which is given by: P = (π^2 E I) / (K L^2), where P is the critical load, E is the modulus of elasticity, I is the moment of inertia, K is the effective length factor, and L is the length of the cylinder.
Introduction to Cylinder Buckling
Cylinder buckling is a critical phenomenon that occurs when a cylinder is subjected to axial compression or external pressure. The buckling behavior of a cylinder is influenced by its geometric parameters, such as the diameter, thickness, and length, as well as its material properties, including the modulus of elasticity and Poisson's ratio. The buckling of a cylinder can be classified into different modes, including axisymmetric and non-axisymmetric buckling. Some key factors that affect cylinder buckling include:
- Geometry: The diameter, thickness, and length of the cylinder all play a role in determining the buckling behavior.
- Material properties: The modulus of elasticity, Poisson's ratio, and yield strength of the material all influence the buckling behavior.
- Loading conditions: The type and magnitude of the load applied to the cylinder can significantly affect the buckling behavior.
Types of Cylinder Buckling
There are several types of cylinder buckling, including axisymmetric and non-axisymmetric buckling. Axisymmetric buckling occurs when the cylinder buckles in a symmetric manner, while non-axisymmetric buckling occurs when the cylinder buckles in an asymmetric manner. Axisymmetric buckling can be further divided into eigenmode and post-buckling behavior. Eigenmode buckling occurs when the cylinder buckles in a single eigenmode, while post-buckling behavior occurs when the cylinder undergoes multiple buckling modes. Some key characteristics of cylinder buckling include:
- Buckling mode: The type of buckling that occurs, such as axisymmetric or non-axisymmetric.
- Buckling load: The load at which the cylinder buckles, which is typically the critical load.
- Post-buckling behavior: The behavior of the cylinder after buckling, which can include post-buckling stiffness and ultimate strength.
Cylinder Buckling Under Axial Compression
Cylinder buckling under axial compression is a common phenomenon that occurs when a cylinder is subjected to a compressive load. The buckling behavior of a cylinder under axial compression is influenced by its geometric parameters, such as the diameter, thickness, and length, as well as its material properties, including the modulus of elasticity and Poisson's ratio. The critical load at which the cylinder buckles can be calculated using the Euler formula. Some key factors that affect cylinder buckling under axial compression include:
- Slenderness ratio: The ratio of the length to the radius of the cylinder, which affects the buckling behavior.
- Material properties: The modulus of elasticity, Poisson's ratio, and yield strength of the material all influence the buckling behavior.
- End conditions: The boundary conditions at the ends of the cylinder, such as fixed or pinned ends, can affect the buckling behavior.
Cylinder Buckling Under External Pressure
Cylinder buckling under external pressure is another common phenomenon that occurs when a cylinder is subjected to an external pressure. The buckling behavior of a cylinder under external pressure is influenced by its geometric parameters, such as the diameter, thickness, and length, as well as its material properties, including the modulus of elasticity and Poisson's ratio. The critical pressure at which the cylinder buckles can be calculated using the Brazier formula. Some key factors that affect cylinder buckling under external pressure include:
- Diameter-to-thickness ratio: The ratio of the diameter to the thickness of the cylinder, which affects the buckling behavior.
- Material properties: The modulus of elasticity, Poisson's ratio, and yield strength of the material all influence the buckling behavior.
- Support conditions: The boundary conditions at the ends of the cylinder, such as fixed or pinned ends, can affect the buckling behavior.
Design Considerations for Cylinder Buckling
The design of a cylinder must take into account the buckling behavior to ensure stability and safety. The design process typically involves calculating the critical load or critical pressure at which the cylinder buckles, and then selecting a safety factor to ensure that the cylinder can withstand the loads and pressures it will be subjected to. Some key design considerations include:
- Material selection: Selecting a material with suitable properties, such as strength and stiffness, to resist buckling.
- Geometry optimization: Optimizing the geometry of the cylinder, such as the diameter, thickness, and length, to minimize the buckling risk.
- Support conditions: Designing the support conditions at the ends of the cylinder, such as fixed or p
What is Euler's formula for buckling?
Euler's formula for buckling is a mathematical equation used to predict the critical load that a slender column can withstand before it begins to buckle. The formula is named after the Swiss mathematician Leonhard Euler, who developed it in the 18th century. The formula is given by:
σ = (π^2 E) / (L^2 / r^2)
where σ is the stress, E is the modulus of elasticity, L is the length of the column, and r is the radius of gyration.
Applications of Euler's Formula
Euler's formula has a wide range of applications in engineering and physics, particularly in the design of structures and machines. Some of the key applications include:
- Column design: Euler's formula is used to determine the critical load that a column can withstand, allowing engineers to design safer and more efficient structures.
- Beam design: The formula can also be applied to beams, where it is used to determine the moment and shear forces that the beam can withstand.
- Structural analysis: Euler's formula is used in finite element analysis to model the behavior of complex structures under various types of loading.
Assumptions and Limitations
Euler's formula is based on several assumptions and has some limitations. Some of the key assumptions include:
- Slender columns: The formula assumes that the column is slender, meaning that its length is much greater than its diameter.
- Homogeneous material: The formula assumes that the material is homogeneous, meaning that its properties are uniform throughout.
- Linear elasticity: The formula assumes that the material behaves in a linear elastic manner, meaning that the stress and strain are proportional.
Derivation of Euler's Formula
Euler's formula can be derived using the theory of elasticity and the equations of motion. The derivation involves:
- Equilibrium equations: The equilibrium equations are used to determine the forces and moments acting on the column.
- Strain-displacement relations: The strain-displacement relations are used to relate the strains to the displacements of the column.
- Constitutive equations: The constitutive equations are used to relate the stresses to the strains of the column.
Comparison with Other Theories
Euler's formula can be compared with other theories, such as the Raleigh-Ritz method and the finite element method. Some of the key differences include:
- Assumptions: The assumptions made in each theory, such as the slenderness of the column and the linearity of the material behavior.
- Accuracy: The accuracy of each theory, with Euler's formula providing a closed-form solution and the other theories providing approximate solutions.
- Computational complexity: The computational complexity of each theory, with Euler's formula being relatively simple and the other theories being more complex.
Extensions and Generalizations
Euler's formula can be extended and generalized to account for various types of loading and boundary conditions. Some of the key extensions include:
- Nonlinear elasticity: The formula can be extended to account for nonlinear elastic behavior, where the stress and strain are not proportional.
- Dynamic loading: The formula can be extended to account for dynamic loading, where the forces and moments vary with time.
- Non-uniform columns: The formula can be generalized to account for non-uniform columns, where the cross-sectional area and moment of inertia vary along the length of the column.
What is the formula for allowable buckling stress?
The formula for allowable buckling stress is given by the Euler's critical load formula, which is a fundamental concept in mechanics of materials. This formula is used to determine the maximum load that a slender column can withstand without buckling. The formula is: F = (π^2 E I) / (K L)^2, where F is the critical load, E is the modulus of elasticity, I is the moment of inertia, K is the effective length factor, and L is the length of the column.
Introduction to Buckling Stress
The concept of buckling stress is crucial in the design of structural elements such as columns, beams, and plates. Buckling occurs when a structure is subjected to a compressive load that causes it to deflect laterally, leading to a loss of stability. The allowable buckling stress is the maximum stress that a structure can withstand without buckling. The formula for allowable buckling stress takes into account the material properties and the geometric parameters of the structure.
- The Euler's critical load formula is used to determine the maximum load that a slender column can withstand without buckling.
- The critical load is the maximum load that a column can withstand without buckling.
- The modulus of elasticity is a measure of the stiffness of a material.
Factors Affecting Buckling Stress
The allowable buckling stress is affected by several factors, including the material properties, geometric parameters, and boundary conditions. The material properties that affect buckling stress include the modulus of elasticity, Poisson's ratio, and the yield strength. The geometric parameters that affect buckling stress include the length, diameter, and thickness of the structure. The boundary conditions that affect buckling stress include the end conditions and the support conditions.
- The material properties that affect buckling stress include the modulus of elasticity and Poisson's ratio.
- The geometric parameters that affect buckling stress include the length and diameter of the structure.
- The boundary conditions that affect buckling stress include the end conditions and the support conditions.
Calculation of Allowable Buckling Stress
The allowable buckling stress can be calculated using the Euler's critical load formula. This formula requires the material properties and geometric parameters of the structure. The allowable buckling stress is then calculated by dividing the critical load by the cross-sectional area of the structure. The allowable buckling stress is an important design parameter that is used to ensure the stability of structural elements.
- The Euler's critical load formula is used to calculate the critical load.
- The critical load is then divided by the cross-sectional area to calculate the allowable buckling stress.
- The allowable buckling stress is an important design parameter that is used to ensure the stability of structural elements.
Applications of Allowable Buckling Stress
The concept of allowable buckling stress has numerous applications in civil engineering, mechanical engineering, and aerospace engineering. The allowable buckling stress is used to design structural elements such as columns, beams, and plates. It is also used to analyze the stability of existing structures and to determine the maximum load that they can withstand.
- The allowable buckling stress is used to design structural elements such as columns and beams.
- The allowable buckling stress is used to analyze the stability of existing structures.
- The allowable buckling stress is used to determine the maximum load that a structure can withstand.
Limitations of Allowable Buckling Stress Formula
The Euler's critical load formula has several limitations that must be considered when calculating the allowable buckling stress. One of the main limitations is that the formula assumes a perfect column with no imperfections. In reality, columns always have some imperfections that can affect their stability. Another limitation is that the formula does not take into account the effects of axial load on the buckling stress.
- The Euler's critical load formula assumes a perfect column with no imperfections.
- The formula does not take into account the effects of axial load on the buckling stress.
- The allowable buckling stress must be adjusted to account for imperfections and axial load effects.
Frequently Asked Questions (FAQs)
What is Compression Buckling in Unstiffened Plates and How is it Calculated?
Compression buckling in unstiffened plates refers to the phenomenon where a plate subjected to compressive forces undergoes a sudden loss of stability, leading to a buckling or wrinkling of the plate. This occurs when the compressive stress exceeds the critical stress of the plate, causing it to deform in a way that is not reversible. The calculation of compression buckling in unstiffened plates involves the use of formulas that take into account the material properties, plate geometry, and boundary conditions. The most commonly used formula for calculating compression buckling in unstiffened plates is the Euler buckling formula, which gives the critical stress as a function of the plate thickness, plate width, and elastic modulus of the material. By using a calculator or software that implements this formula, engineers can quickly and easily determine the critical stress and buckling load for a given plate configuration.
How Does the Formula for Compression Buckling in Unstiffened Plates Account for Different Material Properties?
The formula for compression buckling in unstiffened plates takes into account different material properties such as the elastic modulus, Poisson's ratio, and yield strength. The elastic modulus is a measure of the material's stiffness, and is used to calculate the critical stress. Poisson's ratio is a measure of the material's lateral strain response to axial loading, and is used to account for the transverse deformation of the plate. The yield strength is the maximum stress that the material can withstand without undergoing plastic deformation, and is used to determine the limiting load for the plate. By incorporating these material properties into the formula, engineers can accurately predict the buckling behavior of plates made from different materials, such as steel, aluminum, or composite materials. Additionally, the formula can be modified to account for imperfections in the plate, such as residual stresses or geometric imperfections, which can affect the buckling load and critical stress.
What are the Limitations of the Formula for Compression Buckling in Unstiffened Plates, and How Can They be Addressed?
The formula for compression buckling in unstiffened plates has several limitations, including the assumption of perfect plate geometry and linear elastic material behavior. In reality, plates often have imperfections such as residual stresses, geometric imperfections, or material inhomogeneities, which can affect the buckling load and critical stress. To address these limitations, engineers can use more advanced numerical methods, such as the finite element method, to simulate the buckling behavior of plates with imperfections. Additionally, experimental testing can be used to validate the formula and account for any uncertainties or variabilities in the material properties or plate geometry. By using a combination of theoretical calculations, numerical simulations, and experimental testing, engineers can gain a more complete understanding of the buckling behavior of unstiffened plates and develop more accurate and reliable designs.
How Can the Calculator for Compression Buckling in Unstiffened Plates be Used in Practice, and What are the Benefits of Using it?
The calculator for compression buckling in unstiffened plates can be used in practice to quickly and easily determine the critical stress and buckling load for a given plate configuration. By inputting the plate geometry, material properties, and boundary conditions, engineers can obtain a rapid and accurate estimate of the buckling load and critical stress, which can be used to design and optimize structures such as aircraft, ships, or bridges. The benefits of using the calculator include reduced design time, improved accuracy, and increased reliability, as well as the ability to prove compliance with regulatory requirements and industry standards. Additionally, the calculator can be used to investigate the effects of different design parameters, such as plate thickness or material properties, on the buckling behavior of the plate, allowing engineers to optimize their designs and minimize the risk of buckling or failure. By using the calculator in conjunction with theoretical calculations and experimental testing, engineers can develop more efficient, effective, and reliable designs that meet the requirements of modern engineering applications.
Deja una respuesta

Entradas Relacionadas