Velocity Time Dilation for Object Equation and Calculator
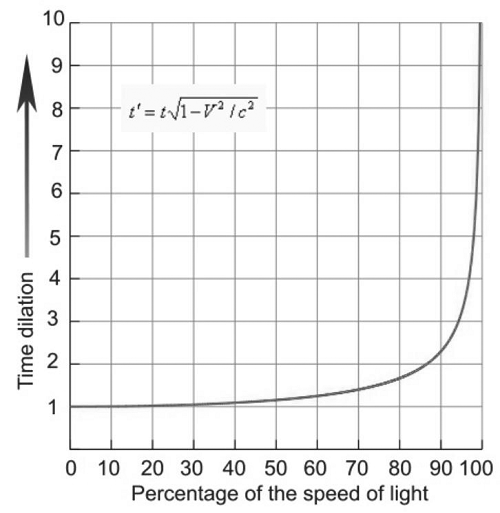
The concept of velocity time dilation is a fundamental aspect of special relativity, describing how time appears to slow down for an object in motion relative to a stationary observer. This phenomenon can be calculated using a specific equation that takes into account the object's velocity and the speed of light. By understanding and applying this equation, physicists and engineers can accurately predict and measure time dilation effects in various scenarios, from high-speed particle collisions to astronomical observations. A velocity time dilation calculator can facilitate these calculations.
- Understanding Velocity Time Dilation for Objects: Equation and Calculator
- How do you solve time dilation for V?
- What is a time dilation calculator?
- How to calculate speed with special relativity?
-
Frequently Asked Questions (FAQs)
- What is Velocity Time Dilation and how does it affect objects in motion?
- How does the Velocity Time Dilation equation relate to the calculator?
- What are the implications of Velocity Time Dilation for our understanding of space and time?
- How can I use the Velocity Time Dilation calculator to explore the effects of special relativity?
Understanding Velocity Time Dilation for Objects: Equation and Calculator
Velocity time dilation is a fundamental concept in physics, particularly in the theory of relativity. It states that the time experienced by an object in motion is slower than the time experienced by a stationary observer. This phenomenon is crucial in understanding the behavior of objects at high speeds, approaching the speed of light.
Introduction to Time Dilation
Time dilation is a consequence of special relativity, which describes the relationship between space and time. According to this theory, the laws of physics are the same for all observers in uniform motion relative to one another. The equation for time dilation is given by: t' = γ(t), where t' is the time experienced by the moving object, t is the time experienced by the stationary observer, and γ is the Lorentz factor, given by γ = 1 / sqrt(1 - v^2/c^2), where v is the velocity of the object and c is the speed of light.
Velocity Time Dilation Equation
The velocity time dilation equation is derived from the Lorentz transformation, which describes the relationship between space and time coordinates in different inertial frames. The equation is: Δt' = γ(Δt), where Δt' is the time interval experienced by the moving object and Δt is the time interval experienced by the stationary observer. This equation shows that the time interval experienced by the moving object is longer than the time interval experienced by the stationary observer.
Calculator for Velocity Time Dilation
A calculator for velocity time dilation can be used to calculate the time dilation factor, γ, and the time interval experienced by the moving object. The calculator typically takes the velocity of the object and the time interval experienced by the stationary observer as input and calculates the time interval experienced by the moving object. The calculator can be used to explore the effects of time dilation on objects at different speeds.
Effects of Velocity Time Dilation on Objects
The effects of velocity time dilation on objects are significant at high speeds, approaching the speed of light. For example, a spaceship traveling at 90% of the speed of light would experience time dilation by a factor of approximately 2.3, meaning that 1 year of time on the spaceship would be equivalent to approximately 2.3 years of time on Earth. The following table summarizes the effects of velocity time dilation on objects at different speeds:
| Velocity | Time Dilation Factor | Effect on Time |
|---|---|---|
| 0.1c | 1.005 | Negligible |
| 0.5c | 1.155 | Moderate |
| 0.9c | 2.294 | Significant |
| 0.99c | 7.088 | Extreme |
The table shows that the time dilation factor increases rapidly as the velocity approaches the speed of light, resulting in significant effects on time.
Applications of Velocity Time Dilation
The concept of velocity time dilation has several practical applications, including GPS technology, particle physics, and astronomy. For example, GPS satellites must account for time dilation due to their high speeds and altitudes, which would result in errors of up to 10 km per day if not corrected. The practical applications of velocity time dilation are a testament to the importance of understanding this fundamental concept in physics.
How do you solve time dilation for V?

To solve time dilation for V, we can use the Lorentz transformation equation, which is a fundamental concept in special relativity. The equation is given by: t' = γ(t - vx/c^2), where t' is the time measured in the moving frame, t is the time measured in the stationary frame, v is the velocity of the moving frame, x is the position of the event, c is the speed of light, and γ is the Lorentz factor.
Understanding Time Dilation
Time dilation occurs when an object moves at a significant fraction of the speed of light. As the object approaches the speed of light, time appears to slow down for an observer watching from a stationary frame. This effect becomes more pronounced as the object approaches the speed of light. To solve for V, we need to rearrange the Lorentz transformation equation to isolate V.
- The Lorentz factor γ is given by 1 / sqrt(1 - v^2/c^2)
- The time dilation factor is given by 1 / γ
- The velocity V can be solved for by rearranging the Lorentz transformation equation
Derivation of the Lorentz Transformation
The Lorentz transformation can be derived from the principles of special relativity. The derivation involves assuming that the laws of physics are the same in all inertial frames and that the speed of light is constant in all inertial frames. The Lorentz transformation can be used to describe the relationship between space and time in different inertial frames.
- The Lorentz transformation is a linear transformation that describes the relationship between space and time in different inertial frames
- The Lorentz transformation can be used to derive the time dilation equation
- The Lorentz transformation is a fundamental concept in special relativity
Time Dilation and Length Contraction
Time dilation is often associated with length contraction, which is another fundamental concept in special relativity. Length contraction occurs when an object moves at a significant fraction of the speed of light and its length appears to shrink in the direction of motion.
- Length contraction occurs when an object moves at a significant fraction of the speed of light
- Time dilation and length contraction are both consequences of the Lorentz transformation
- The Lorentz transformation can be used to describe both time dilation and length contraction
Experimental Evidence for Time Dilation
There is a significant amount of experimental evidence that supports the concept of time dilation. One of the most famous experiments is the Hafele-Keating experiment, which measured the time dilation effect on atomic clocks flown around the Earth on commercial airliners.
- The Hafele-Keating experiment measured the time dilation effect on atomic clocks
- The experiment confirmed the predictions of special relativity
- The time dilation effect has been observed in many other experiments
Time Dilation in Astrophysics
Time dilation has significant implications for astrophysics, particularly in the study of black holes and neutron stars. The strong gravitational field of a black hole causes time dilation to occur, which can affect the observed behavior of these objects.
- Time dilation occurs in the strong gravitational field of a black hole
- The time dilation effect can affect the observed behavior of black holes and neutron stars
- Time dilation is an important concept in the study of astrophysics
What is a time dilation calculator?
A time dilation calculator is a tool used to calculate the effect of time dilation on an object or a person in a specific situation. Time dilation is a fundamental concept in physics, particularly in the theory of relativity, which states that the passage of time can vary depending on the object's speed and its proximity to a gravitational field. The calculator takes into account the object's velocity and its position in a gravitational field to calculate the amount of time that has passed for the object relative to a stationary observer.
How Time Dilation Calculators Work
Time dilation calculators work by using the Lorentz factor to calculate the time dilation effect. The Lorentz factor is a mathematical formula that describes how time and space are affected by an object's velocity and gravitational field. The calculator uses the following formula: t' = t / sqrt(1 - v^2/c^2), where t' is the time measured by the moving observer, t is the time measured by the stationary observer, v is the velocity of the moving observer, and c is the speed of light. Some key features of time dilation calculators include:
- Calculating time dilation for objects moving at high speeds
- Calculating time dilation for objects in strong gravitational fields
- Comparing the time measured by a moving observer to the time measured by a stationary observer
Applications of Time Dilation Calculators
Time dilation calculators have several practical applications in physics and engineering. They can be used to calculate the time dilation effect on GPS satellites, which must account for time dilation to provide accurate location and time information. They can also be used to calculate the time dilation effect on high-speed particles in particle accelerators. Some other applications of time dilation calculators include:
- Calculating the time dilation effect on cosmic rays and other high-energy particles
- Calculating the time dilation effect on black holes and other strong gravitational fields
- Designing timekeeping systems for high-speed vehicles and spacecraft
Limitations of Time Dilation Calculators
Time dilation calculators have several limitations that must be considered when using them. One limitation is that they assume a constant velocity and a constant gravitational field, which may not be the case in real-world situations. They also assume that the object is moving in a straight line, which may not be the case for objects moving in complex trajectories. Some other limitations of time dilation calculators include:
- Ignoring the effects of acceleration on time dilation
- Ignoring the effects of non-uniform gravitational fields on time dilation
- Assuming a classical concept of time and ignoring quantum effects
Types of Time Dilation Calculators
There are several types of time dilation calculators available, each with its own strengths and weaknesses. Some calculators are designed for special relativity and calculate the time dilation effect for objects moving at high speeds. Others are designed for general relativity and calculate the time dilation effect for objects in strong gravitational fields. Some other types of time dilation calculators include:
- Online calculators that can be accessed through a web browser
- Mobile apps that can be downloaded to a smartphone or tablet
- Desktop applications that can be installed on a computer
Uses of Time Dilation Calculators in Education
Time dilation calculators can be a useful tool for educators and students to learn about the concept of time dilation. They can be used to illustrate the effects of special relativity and general relativity on time and space. They can also be used to design experiments and simulations that demonstrate the time dilation effect. Some other uses of time dilation calculators in education include:
- Teaching the concept of time dilation and its relation to relativity
- Designing labs and experiments to demonstrate the time dilation effect
- Developing interactive simulations that illustrate the effects of time dilation
How to calculate speed with special relativity?

To calculate speed with special relativity, we need to consider the Lorentz transformation, which describes how space and time coordinates are affected by relative motion. The Lorentz transformation can be used to derive the relativistic velocity equation, which takes into account the speed of light and the relative velocity between two inertial frames.
Introduction to Relativistic Velocity
The relativistic velocity equation is a fundamental concept in special relativity, as it describes how velocity is affected by relative motion. To calculate relativistic velocity, we need to use the Lorentz transformation, which is given by:
- The Lorentz transformation equation for time dilation: t' = γ(t - vx/c^2)
- The Lorentz transformation equation for length contraction: x' = γ(x - vt)
- The relativistic velocity equation: v' = (v + u) / (1 + vu/c^2)
These equations show how time and length are affected by relative motion, and how velocity is transformed between different inertial frames.
Time Dilation and Length Contraction
Time dilation and length contraction are two fundamental effects of special relativity, which describe how time and length are affected by relative motion. To calculate time dilation and length contraction, we need to use the Lorentz transformation equations:
- The time dilation equation: t' = γt
- The length contraction equation: x' = x / γ
- The Lorentz factor equation: γ = 1 / sqrt(1 - v^2/c^2)
These equations show how time and length are affected by relative motion, and how the Lorentz factor is used to calculate time dilation and length contraction.
Relativistic Velocity Addition
The relativistic velocity addition equation is used to calculate the resultant velocity of two objects moving at relativistic speeds. To calculate relativistic velocity addition, we need to use the Lorentz transformation equation:
- The relativistic velocity addition equation: v' = (v + u) / (1 + vu/c^2)
- The velocity equation for the first object: v = dx/dt
- The velocity equation for the second object: u = dx'/dt'
These equations show how velocity is transformed between different inertial frames, and how the relativistic velocity addition equation is used to calculate the resultant velocity.
Relativistic Mass and Energy
The relativistic mass and energy equations are used to calculate the mass and energy of an object moving at relativistic speeds. To calculate relativistic mass and energy, we need to use the Lorentz transformation equations:
- The relativistic mass equation: m' = γm
- The relativistic energy equation: E' = γmc^2
- The Lorentz factor equation: γ = 1 / sqrt(1 - v^2/c^2)
These equations show how mass and energy are affected by relative motion, and how the Lorentz factor is used to calculate relativistic mass and energy.
Applications of Special Relativity
Special relativity has many practical applications, including particle physics, nuclear physics, and astronomy. To apply special relativity to these fields, we need to use the Lorentz transformation equations and the relativistic velocity addition equation:
- The particle physics application: calculating the relativistic velocity of particles in a particle accelerator
- The nuclear physics application: calculating the relativistic energy of nuclear reactions
- The astronomy application: calculating the redshift of light from distant galaxies
These applications show how special relativity is used to calculate relativistic velocity, relativistic energy, and redshift, and how these calculations are used to understand high-energy phenomena.
Frequently Asked Questions (FAQs)
What is Velocity Time Dilation and how does it affect objects in motion?
Velocity Time Dilation is a fundamental concept in physics that describes the phenomenon where the passage of time is affected by an object's velocity. According to special relativity, as an object approaches the speed of light, time appears to slow down for an observer watching from a stationary frame of reference. This effect, known as time dilation, becomes more pronounced as the object's velocity increases. The equation for Velocity Time Dilation is given by t = γ(t'), where t is the time measured by the stationary observer, t' is the time measured by the moving object, and γ is the Lorentz factor, which depends on the object's velocity and the speed of light. This concept has been extensively tested and confirmed through various experiments and observations, and has far-reaching implications for our understanding of space and time.
How does the Velocity Time Dilation equation relate to the calculator?
The Velocity Time Dilation equation is closely related to the calculator, as it provides the mathematical framework for calculating the effects of time dilation on objects in motion. The calculator takes the object's velocity and the time measured by the moving object as inputs, and uses the Lorentz factor to calculate the time measured by the stationary observer. The calculator can be used to simulate a wide range of scenarios, from high-speed particles to spacecraft traveling at significant fractions of the speed of light. By using the calculator, users can gain a deeper understanding of how Velocity Time Dilation affects the behavior of objects in motion, and explore the fascinating consequences of special relativity. The calculator is an essential tool for physicists, engineers, and anyone interested in exploring the frontiers of physics and astronomy.
What are the implications of Velocity Time Dilation for our understanding of space and time?
The implications of Velocity Time Dilation are profound and far-reaching, challenging our classical notions of space and time. According to special relativity, time is not an absolute quantity, but rather a relative concept that depends on the observer's frame of reference. This means that time can appear to slow down or speed up, depending on the observer's velocity and position. The equation for Velocity Time Dilation provides a quantitative description of this effect, allowing us to predict and simulate the behavior of objects in motion. The implications of Velocity Time Dilation are not limited to physics, but also have significant consequences for our understanding of cosmology, astronomy, and the universe as a whole. By studying Velocity Time Dilation, scientists can gain insights into the nature of space and time, and develop new theories and models to describe the behavior of the universe.
How can I use the Velocity Time Dilation calculator to explore the effects of special relativity?
To use the Velocity Time Dilation calculator, simply enter the object's velocity and the time measured by the moving object, and the calculator will output the time measured by the stationary observer. You can then experiment with different velocities and times to see how the effects of time dilation change. The calculator also allows you to simulate a wide range of scenarios, from low-speed objects to high-speed particles approaching the speed of light. By using the calculator, you can gain a deeper understanding of how Velocity Time Dilation affects the behavior of objects in motion, and explore the fascinating consequences of special relativity. You can also use the calculator to test your understanding of the equation and to visualize the effects of time dilation in different frames of reference. Whether you are a student, a teacher, or simply a curious individual, the Velocity Time Dilation calculator is a powerful tool for exploring the frontiers of physics and astronomy.
Deja una respuesta


Entradas Relacionadas