Trapezoid Torque Deformation Stress Equations and Calculator
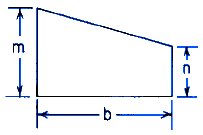
The Trapezoid Torque Deformation Stress Equations and Calculator is a valuable tool for engineers and designers to calculate the stress and deformation of trapezoidal shapes under various loads. Trapezoids are commonly used in construction, machinery, and other structural applications, and understanding their behavior under torque is crucial for safe and efficient design. This article provides a comprehensive overview of the equations and calculator used to determine the stress and deformation of trapezoids, enabling professionals to make informed decisions and ensure the integrity of their designs. The calculator simplifies complex calculations, saving time and reducing errors.
- Trapezoid Torque Deformation Stress Equations and Calculator
-
Understanding Trapezoid Torque Deformation Stress Equations and Calculator
- Introduction to Trapezoid Geometry and Its Significance in Engineering
- Derivation of Trapezoid Torque Deformation Stress Equations
- Application of Trapezoid Torque Deformation Stress Equations in Real-World Problems
- Limitations and Assumptions of Trapezoid Torque Deformation Stress Equations
- Future Developments and Advancements in Trapezoid Torque Deformation Stress Equations and Calculator
-
Frequently Asked Questions (FAQs)
- What is Trapezoid Torque Deformation Stress and how is it calculated?
- How do I use the Trapezoid Torque Deformation Stress Equations and Calculator?
- What are the limitations and assumptions of the Trapezoid Torque Deformation Stress Equations and Calculator?
- How can I apply the Trapezoid Torque Deformation Stress Equations and Calculator to real-world problems?
Trapezoid Torque Deformation Stress Equations and Calculator
The Trapezoid Torque Deformation Stress Equations and Calculator is a tool used to calculate the stress and deformation of a trapezoid-shaped object under torque. This calculator is widely used in the field of mechanical engineering to design and analyze machinery and structures. The calculator takes into account the dimensions of the trapezoid, the material properties, and the torque applied to calculate the stress and deformation.
Introduction to Trapezoid Torque Deformation Stress Equations
The Trapezoid Torque Deformation Stress Equations are used to calculate the stress and deformation of a trapezoid-shaped object under torque. These equations are based on the theory of mechanics and take into account the dimensions of the trapezoid, the material properties, and the torque applied. The equations are used to calculate the maximum stress, maximum deformation, and safety factor of the trapezoid.
Material Properties and Dimensions
The material properties and dimensions of the trapezoid are critical inputs in the Trapezoid Torque Deformation Stress Equations and Calculator. The material properties include the young's modulus, poisson's ratio, and yield strength of the material. The dimensions of the trapezoid include the length, width, and height of the trapezoid. These inputs are used to calculate the stress and deformation of the trapezoid.
Torque and Load Calculation
The torque and load calculation is a critical step in the Trapezoid Torque Deformation Stress Equations and Calculator. The torque is calculated using the formula: T = F x r, where T is the torque, F is the force, and r is the radius of the trapezoid. The load is calculated using the formula: L = F / A, where L is the load, F is the force, and A is the area of the trapezoid.
Stress and Deformation Calculation
The stress and deformation calculation is the final step in the Trapezoid Torque Deformation Stress Equations and Calculator. The stress is calculated using the formula: σ = F / A, where σ is the stress, F is the force, and A is the area of the trapezoid. The deformation is calculated using the formula: δ = σ / E, where δ is the deformation, σ is the stress, and E is the young's modulus of the material.
Applications and Limitations
The Trapezoid Torque Deformation Stress Equations and Calculator has a wide range of applications in the field of mechanical engineering. It is used to design and analyze machinery and structures. However, the calculator has some limitations, including the assumption of a linear elastic material and the neglect of dynamic effects. The calculator is also sensitive to input errors, and small errors in the input can result in large errors in the output.
| Parameter | Unit | Description |
|---|---|---|
| Length | m | The length of the trapezoid |
| Width | m | The width of the trapezoid |
| Height | m | The height of the trapezoid |
| Young's Modulus | Pa | The young's modulus of the material |
| Poisson's Ratio | - | The poisson's ratio of the material |
Understanding Trapezoid Torque Deformation Stress Equations and Calculator
The understanding of trapezoid structures under torque and deformation stresses is crucial in various engineering applications, including mechanical, civil, and aerospace engineering. The calculator designed for these equations simplifies the process of determining the stress and strain on trapezoidal shapes, which is essential for ensuring the structural integrity and reliability of the systems in which these shapes are used.
Introduction to Trapezoid Geometry and Its Significance in Engineering
The geometry of a trapezoid is characterized by its four sides, where two sides are parallel and two are non-parallel. This geometric shape is commonly found in various engineering structures, such as bridge components, building frames, and mechanical linkages. The significance of trapezoids in engineering lies in their ability to provide structural stability and support under various types of loads, including torque and deformation. Understanding the equations that govern the behavior of trapezoids under these loads is essential for the design and analysis of such structures.
Derivation of Trapezoid Torque Deformation Stress Equations
The derivation of torque deformation stress equations for trapezoids involves complex mathematical formulations that take into account the geometry of the trapezoid, the material properties, and the loading conditions. The equations are based on the principles of mechanics of materials, which involve the relationship between stress, strain, and deformation. The derivation process typically starts with the assumption of a linear elastic behavior of the material, followed by the application of equilibrium equations and compatibility conditions to obtain the stress and strain distributions within the trapezoid.
Application of Trapezoid Torque Deformation Stress Equations in Real-World Problems
The application of trapezoid torque deformation stress equations is diverse and widespread in various engineering disciplines. For instance, in mechanical engineering, these equations are used to design and analyze gear systems, shafts, and bearings that are subject to torque and deformation loads. In civil engineering, the equations are applied to the design of bridge components, such as beams and girders, that are exposed to wind and seismic loads. The calculator designed for these equations enables engineers to quickly and accurately determine the stress and strain on trapezoidal structures, allowing for the optimization of their design and ensuring their safety and reliability.
Limitations and Assumptions of Trapezoid Torque Deformation Stress Equations
The limitations and assumptions of trapezoid torque deformation stress equations are crucial considerations in their application. One of the primary assumptions is that the material behavior is linear elastic, which may not always be the case in practice. Additionally, the equations assume that the loading conditions are static or quasi-static, which may not account for dynamic loads. The calculator designed for these equations should also account for these limitations and assumptions, providing warnings or flags when the input parameters exceed the valid range of the equations.
Future Developments and Advancements in Trapezoid Torque Deformation Stress Equations and Calculator
The future developments and advancements in trapezoid torque deformation stress equations and calculator are expected to focus on non-linear material behavior, dynamic loading conditions, and multi-physics problems. The integration of finite element methods and computational mechanics may also enhance the accuracy and versatility of the equations and the calculator. Furthermore, the incorporation of machine learning and artificial intelligence techniques may enable the development of more robust and user-friendly calculators that can handle complex trapezoid geometries and loading conditions. The advancements in these areas will have a significant impact on the design and analysis of trapezoidal structures, leading to more efficient, safe, and reliable systems.
Frequently Asked Questions (FAQs)
What is Trapezoid Torque Deformation Stress and how is it calculated?
Trapezoid torque deformation stress refers to the stress and deformation that occurs in a trapezoid shape when it is subjected to torque or a twisting force. The calculation of trapezoid torque deformation stress involves the use of mathematical equations that take into account the geometric properties of the trapezoid, such as its height, width, and thickness, as well as the material properties, such as its elastic modulus and poisson's ratio. The equations used to calculate trapezoid torque deformation stress are based on the theory of elasticity and the principles of mechanics of materials. The calculator for trapezoid torque deformation stress is a tool that can be used to simplify the calculation process and provide accurate results.
How do I use the Trapezoid Torque Deformation Stress Equations and Calculator?
To use the trapezoid torque deformation stress equations and calculator, you need to input the required parameters, such as the geometric properties of the trapezoid, the material properties, and the torque or twisting force applied to the trapezoid. The calculator will then use these inputs to calculate the stress and deformation of the trapezoid. The equations used in the calculator are based on the theory of elasticity and the principles of mechanics of materials, and they take into account the complexities of the trapezoid shape. The results provided by the calculator will include the maximum stress and deformation of the trapezoid, as well as the location of the maximum stress and deformation. The calculator can be used to analyze and design trapezoid shapes that are subjected to torque or twisting forces, and it can help to optimize the design for strength and stiffness.
What are the limitations and assumptions of the Trapezoid Torque Deformation Stress Equations and Calculator?
The trapezoid torque deformation stress equations and calculator are based on several assumptions and limitations, including the assumption of linear elasticity and the neglect of non-linear effects such as plasticity and creep. The calculator also assumes that the trapezoid shape is uniform and symmetric, and that the torque or twisting force is uniformly distributed. Additionally, the calculator does not take into account other effects such as temperature, corrosion, and fatigue, which can affect the stress and deformation of the trapezoid. The results provided by the calculator should be interpreted with caution, and consideration should be given to the limitations and assumptions of the equations and calculator. The calculator should be used as a tool to aid in the design and analysis of trapezoid shapes, but it should not be relied upon as the sole means of evaluation.
How can I apply the Trapezoid Torque Deformation Stress Equations and Calculator to real-world problems?
The trapezoid torque deformation stress equations and calculator can be applied to a wide range of real-world problems, including the design and analysis of mechanical components such as gears, shafts, and bearings. The calculator can be used to evaluate the stress and deformation of these components under torque or twisting forces, and to optimize their design for strength and stiffness. The equations and calculator can also be used in the analysis of structural components such as beams and columns, which are subjected to torque or twisting forces. Additionally, the calculator can be used in the design and analysis of machinery and equipment that are subjected to torque or twisting forces, such as pumps, motors, and gearboxes. The results provided by the calculator can be used to inform the design process, and to ensure that the components or structures are safe and reliable. The calculator can also be used to evaluate the effects of different materials and designs on the stress and deformation of trapezoid shapes, and to identify the most optimal design for a given application.
Deja una respuesta

Entradas Relacionadas