Thick Wall Cylinder Press or Shrink Fits Equations and Calculator

The Thick Wall Cylinder Press or Shrink Fits is a critical concept in engineering, particularly in the design and manufacture of cylindrical components. It involves the calculation of stresses and strains in thick-walled cylinders subjected to internal or external pressures. This article provides a comprehensive overview of the equations and calculations involved in determining the stresses and strains in thick-walled cylinders, along with a calculator to simplify the process, ensuring accurate and efficient design of cylindrical components. The equations and calculator are essential tools for engineers and designers.
- Thick Wall Cylinder Press or Shrink Fits Equations and Calculator: A Comprehensive Overview
- What is the tolerance for shrink fittings?
- What is the shear stress of a thick-walled cylinder?
- What is the criteria for a thick cylinder?
- Do the Lamé equations predict the stress and strain in thick cylinders?
-
Frequently Asked Questions (FAQs)
- What is the purpose of the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator?
- How do the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator account for the effects of shrink fits?
- What are the key assumptions and limitations of the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator?
- How can the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator be used in real-world engineering applications?
Thick Wall Cylinder Press or Shrink Fits Equations and Calculator: A Comprehensive Overview
The thick wall cylinder press or shrink fits equations and calculator are essential tools in engineering and mechanics, particularly in the design and manufacture of cylindrical components. These equations and calculators help determine the stress and strain on the cylinder due to internal or external pressure, as well as the interference fit between the cylinder and other components.
Introduction to Thick Wall Cylinder Press or Shrink Fits
The thick wall cylinder press or shrink fits refer to the process of fitting two cylindrical components together with a tight interference fit. This is achieved by heating or cooling one of the components to create a thermal expansion or contraction, allowing for a precise fit. The equations and calculator for thick wall cylinder press or shrink fits help engineers determine the required interference and clearance between the components.
Thick Wall Cylinder Press or Shrink Fits Equations
The equations for thick wall cylinder press or shrink fits involve the calculation of hoop stress, radial stress, and axial stress on the cylinder. These equations take into account the internal pressure, external pressure, and material properties of the cylinder. The Lame equations are commonly used to calculate the stress and strain on the cylinder.
Calculator for Thick Wall Cylinder Press or Shrink Fits
The calculator for thick wall cylinder press or shrink fits is a useful tool for engineers to quickly determine the required interference and clearance between components. The calculator takes into account the cylinder dimensions, material properties, and pressure values to calculate the stress and strain on the cylinder. The calculator can also be used to determine the safety factor and factor of safety for the design.
Applications of Thick Wall Cylinder Press or Shrink Fits
The thick wall cylinder press or shrink fits have numerous applications in various industries, including aerospace, automotive, and energy. These applications include the manufacture of engine components, gearboxes, and bearings. The high-precision fit required in these applications can be achieved using the equations and calculator for thick wall cylinder press or shrink fits.
Limitations and Considerations of Thick Wall Cylinder Press or Shrink Fits
The thick wall cylinder press or shrink fits have several limitations and considerations that must be taken into account. These include the material properties, cylinder dimensions, and pressure values. The thermal expansion and contraction of the components must also be considered to ensure a precise fit. The following table summarizes the key considerations:
| Parameter | Unit | Description |
|---|---|---|
| Internal Pressure | psi | The pressure inside the cylinder |
| External Pressure | psi | The pressure outside the cylinder |
| Cylinder Dimensions | in | The diameter and length of the cylinder |
| Material Properties | ksi | The yield strength and ultimate strength of the material |
| Interference | in | The difference in diameter between the two components |
The stress and strain on the cylinder can be calculated using the Lame equations, which take into account the internal pressure, external pressure, and material properties. The calculator can be used to determine the required interference and clearance between components, as well as the safety factor and factor of safety for the design.
What is the tolerance for shrink fittings?
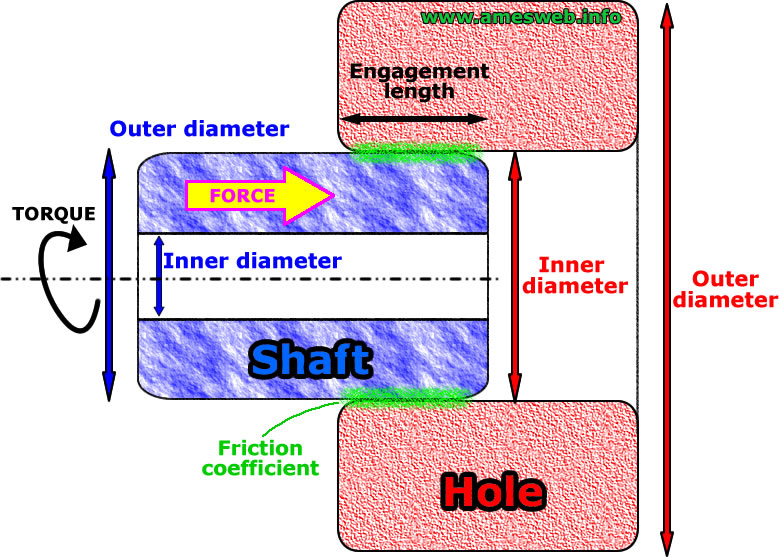
The tolerance for shrink fittings is a critical factor in ensuring the proper fit and function of the assembled parts. The tolerance refers to the acceptable range of deviation from the nominal dimension of the parts. In general, the tolerance for shrink fittings is typically quite tight, as the parts must fit together with a high degree of precision to ensure proper interference and stability.
Understanding Shrink Fitting Tolerances
The tolerance for shrink fittings is influenced by several factors, including the material properties, temperature, and manufacturing process. To achieve the desired tolerance, manufacturers must carefully control the dimensions and surface finish of the parts. Some key considerations include:
- The thermal expansion of the materials, which can affect the fit of the parts
- The surface roughness, which can impact the friction and wear of the parts
- The geometry of the parts, including the diameter, length, and shape
Factors Affecting Shrink Fitting Tolerances
Several factors can affect the tolerance for shrink fittings, including the design of the parts, the manufacturing process, and the environmental conditions. For example, temperature and humidity can impact the dimensional stability of the parts, while vibration and impact can affect the interference fit. Some key factors to consider include:
- The coefficient of thermal expansion, which can affect the fit of the parts
- The yield strength and ultimate strength of the materials, which can impact the stability of the assembly
- The surface treatment, such as plating or coating, which can affect the friction and wear of the parts
Measuring Shrink Fitting Tolerances
Measuring the tolerance for shrink fittings requires careful inspection and measurement of the parts. This can involve using precision instruments, such as micrometers and calipers, to measure the dimensions and surface finish of the parts. Some key considerations include:
- The measurement uncertainty, which can affect the accuracy of the results
- The sampling plan, which can impact the representativeness of the data
- The data analysis, which can help to identify trends and patterns in the data
Controlling Shrink Fitting Tolerances
Controlling the tolerance for shrink fittings requires careful planning and execution of the manufacturing process. This can involve using statistical process control (SPC) and total quality management (TQM) techniques to monitor and adjust the process. Some key considerations include:
- The process capability, which can affect the ability to produce parts within the desired tolerance
- The process control, which can impact the stability and consistency of the process
- The operator training, which can affect the skill level and knowledge of the production staff
Specifications for Shrink Fitting Tolerances
Specifications for shrink fitting tolerances can vary depending on the industry and application. However, some common standards and guidelines can provide a starting point for design and manufacturing. Some key considerations include:
- The ASME and ANSI standards for dimensional tolerancing
- The ISO and DIN standards for geometrical product specification
- The MIL-STD and NASA standards for aerospace and defense applications
What is the shear stress of a thick-walled cylinder?

The shear stress of a thick-walled cylinder can be calculated using the Lame's equations, which describe the stress distribution in a cylinder under internal and external pressure. The shear stress is a critical parameter in the design of cylinders, as it can lead to failure if it exceeds the material's yield strength.
Introduction to Shear Stress in Thick-Walled Cylinders
The shear stress in a thick-walled cylinder is caused by the tangential forces that act on the cylinder's wall. These forces are a result of the pressure difference between the inside and outside of the cylinder. To calculate the shear stress, we need to consider the radial stress, tangential stress, and axial stress. The key factors that influence the shear stress are:
- Internal pressure: The pressure inside the cylinder, which causes the cylinder to expand.
- External pressure: The pressure outside the cylinder, which causes the cylinder to compress.
- Wall thickness: The thickness of the cylinder's wall, which affects the stress distribution.
Calculating Shear Stress in Thick-Walled Cylinders
To calculate the shear stress in a thick-walled cylinder, we can use the Lame's equations, which are:
- Radial stress: σr = (P1 R1^2 - P2 R2^2) / (R2^2 - R1^2) + (P1 - P2) / (2 (R2^2 - R1^2)) (2 R1^2 ln(R2/R1) + R2^2 - R1^2)
- Tangential stress: σθ = (P1 R1^2 - P2 R2^2) / (R2^2 - R1^2) - (P1 - P2) / (2 (R2^2 - R1^2)) (2 R1^2 ln(R2/R1) + R2^2 - R1^2)
- Axial stress: σz = (P1 R1^2 - P2 R2^2) / (R2^2 - R1^2)
where P1 and P2 are the internal and external pressures, R1 and R2 are the inner and outer radii, and σr, σθ, and σz are the radial, tangential, and axial stresses, respectively.
Factors Affecting Shear Stress in Thick-Walled Cylinders
The shear stress in a thick-walled cylinder is affected by several factors, including:
- Material properties: The yield strength, ultimate strength, and modulus of elasticity of the material.
- Geometric parameters: The inner radius, outer radius, and wall thickness of the cylinder.
- Loading conditions: The internal pressure, external pressure, and temperature.
These factors can be used to optimize the design of the cylinder and minimize the shear stress.
Design Considerations for Thick-Walled Cylinders
When designing a thick-walled cylinder, it is essential to consider the shear stress and other stress components to ensure the cylinder can withstand the applied loads. The design should take into account the material properties, geometric parameters, and loading conditions. The shear stress can be minimized by:
- Increasing the wall thickness: To reduce the stress concentration.
- Using a stronger material: To increase the yield strength and ultimate strength.
- Optimizing the geometric parameters: To minimize the stress concentration.
Applications of Thick-Walled Cylinders
Thick-walled cylinders are used in various industries, including:
- Pressure vessels: To store gases and liquids under high pressure.
- Pipelines: To transport fluids and gases over long distances.
- Aerospace: To design lightweight and high-strength components.
The shear stress is a critical parameter in the design of these cylinders, as it can affect the structural integrity and safety of the system.
What is the criteria for a thick cylinder?

The criteria for a thick cylinder is typically defined by its wall thickness and radius. A thick cylinder is one where the wall thickness is significant compared to the radius, and the stress and strain distributions are not uniform across the wall. This is in contrast to a thin cylinder, where the wall thickness is relatively small compared to the radius, and the stress and strain distributions can be approximated as uniform.
Definition of a Thick Cylinder
A thick cylinder is defined as one where the wall thickness is greater than or equal to 10% of the radius. This means that the cylinder has a significant amount of material in its wall, which affects the stress and strain distributions. Some key points to consider when defining a thick cylinder include:
- The radius of the cylinder, which determines the overall size of the cylinder
- The wall thickness, which determines the amount of material in the cylinder's wall
- The material properties, such as the elastic modulus and Poisson's ratio, which affect the cylinder's behavior under load
Stress and Strain Distributions
In a thick cylinder, the stress and strain distributions are not uniform across the wall. The hoop stress, which is the stress that acts circumferentially around the cylinder, is typically higher at the inner surface of the cylinder than at the outer surface. This is due to the fact that the pressure inside the cylinder acts on the inner surface, causing it to experience a higher stress. Some key points to consider when analyzing the stress and strain distributions in a thick cylinder include:
- The hoop stress, which is the stress that acts circumferentially around the cylinder
- The axial stress, which is the stress that acts longitudinally along the cylinder
- The radial stress, which is the stress that acts radially outward from the center of the cylinder
Material Properties
The material properties of a thick cylinder, such as the elastic modulus and Poisson's ratio, play a critical role in determining its behavior under load. The elastic modulus determines the stiffness of the material, while Poisson's ratio determines the amount of deformation that occurs in the material. Some key points to consider when selecting a material for a thick cylinder include:
- The elastic modulus, which determines the stiffness of the material
- The Poisson's ratio, which determines the amount of deformation that occurs in the material
- The yield strength, which determines the maximum stress that the material can withstand before deforming plastically
Design Considerations
When designing a thick cylinder, there are several design considerations that must be taken into account. These include the pressure inside the cylinder, the temperature of the cylinder, and the corrosion resistance of the material. Some key points to consider when designing a thick cylinder include:
- The pressure inside the cylinder, which determines the stress and strain distributions
- The temperature of the cylinder, which affects the material properties and the stress and strain distributions
- The corrosion resistance of the material, which affects the durability of the cylinder
Applications of Thick Cylinders
Thick cylinders have a wide range of applications, including pressure vessels, pipelines, and storage tanks. They are often used in high-pressure and high-temperature applications, where the stress and strain distributions are critical. Some key points to consider when selecting a thick cylinder for a particular application include:
- The pressure rating of the cylinder, which determines its ability to withstand high-pressure applications
- The temperature rating of the cylinder, which determines its ability to withstand high-temperature applications
- The corrosion resistance of the material, which affects the durability of the cylinder
Do the Lamé equations predict the stress and strain in thick cylinders?

The Lamé equations are a set of partial differential equations used to describe the stress and strain distributions in elastic solids. In the context of thick cylinders, the Lamé equations can be applied to predict the stress and strain distributions under various loading conditions. The equations are based on the theory of elasticity and take into account the material properties and boundary conditions of the cylinder. By solving the Lamé equations, engineers can determine the stress and strain distributions in the cylinder, which is essential for designing and analyzing structures that are subject to various types of loading.
Introduction to Lamé Equations in Cylinder Analysis
The Lamé equations are a fundamental tool for analyzing the mechanical behavior of thick cylinders. To apply these equations, engineers need to consider the cylinder's geometry, material properties, and boundary conditions. The equations are typically solved using numerical methods, such as the finite element method. The solution provides a detailed description of the stress and strain distributions in the cylinder, allowing engineers to identify potential failure modes and optimize the design. Some key considerations when applying the Lamé equations to cylinder analysis include:
- Boundary conditions: The boundary conditions, such as the loading and support conditions, must be carefully defined to ensure accurate results.
- Material properties: The material properties, such as the Young's modulus and Poisson's ratio, must be accurately determined to ensure reliable results.
- Cylinder geometry: The cylinder geometry, including the radius, thickness, and length, must be carefully defined to ensure accurate results.
Lamé Equations for Thick Cylinders Under Axial Loading
When a thick cylinder is subjected to axial loading, the Lamé equations can be used to predict the stress and strain distributions. The equations take into account the material properties and boundary conditions of the cylinder. By solving the equations, engineers can determine the stress and strain distributions in the cylinder, including the axial stress, radial stress, and hoop stress. The solution can be used to identify potential failure modes, such as yielding or buckling. Some key considerations when applying the Lamé equations to axial loading include:
- Axial load: The axial load must be carefully defined, including the magnitude and distribution of the load.
- Material properties: The material properties, such as the Young's modulus and Poisson's ratio, must be accurately determined to ensure reliable results.
- Cylinder geometry: The cylinder geometry, including the radius, thickness, and length, must be carefully defined to ensure accurate results.
Lamé Equations for Thick Cylinders Under Torsional Loading
When a thick cylinder is subjected to torsional loading, the Lamé equations can be used to predict the stress and strain distributions. The equations take into account the material properties and boundary conditions of the cylinder. By solving the equations, engineers can determine the stress and strain distributions in the cylinder, including the shear stress and strain. The solution can be used to identify potential failure modes, such as yielding or fracture. Some key considerations when applying the Lamé equations to torsional loading include:
- Torsional load: The torsional load must be carefully defined, including the magnitude and distribution of the load.
- Material properties: The material properties, such as the shear modulus and Poisson's ratio, must be accurately determined to ensure reliable results.
- Cylinder geometry: The cylinder geometry, including the radius, thickness, and length, must be carefully defined to ensure accurate results.
Assumptions and Limitations of the Lamé Equations
The Lamé equations are based on several assumptions and limitations, which must be carefully considered when applying the equations to thick cylinder analysis. Some key assumptions include:
- Linear elasticity: The material behavior is assumed to be linear elastic, meaning that the stress and strain are related by a linear relationship.
- Small deformations: The deformations are assumed to be small, meaning that the strain is relatively small compared to the size of the cylinder.
- Homogeneous material: The material is assumed to be homogeneous, meaning that the material properties are uniform throughout the cylinder.
Conclusion and Future Work in Lamé Equations for Cylinder Analysis
The Lamé equations provide a powerful tool for analyzing the mechanical behavior of thick cylinders. However, there are several areas for future work, including:
- Nonlinear material behavior: The development of nonlinear material models that can accurately capture the behavior of materials under large deformations.
- Inhomogeneous materials: The development of models that can accurately capture the behavior of inhomogeneous materials, such as composites or functionally graded materials.
- Multiscale analysis: The development of multiscale models that can capture the behavior of cylinders at multiple length scales, from the microscale to the macroscale.
Frequently Asked Questions (FAQs)
What is the purpose of the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator?
The Thick Wall Cylinder Press or Shrink Fits Equations and Calculator is a tool used to calculate the stress and strain on a thick-walled cylinder when it is subjected to internal pressure or external pressure. The calculator takes into account the material properties of the cylinder, such as its elastic modulus and poisson's ratio, as well as the dimensions of the cylinder, including its inner radius, outer radius, and length. The calculator can be used to determine the safety factor of the cylinder, which is the ratio of the yield strength of the material to the maximum stress on the cylinder. This information is critical in designing and analyzing pressure vessels, pipes, and other cylindrical structures that are subjected to high pressures. By using the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator, engineers can ensure that their designs are safe and reliable, and that they meet the required standards and regulations.
How do the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator account for the effects of shrink fits?
The Thick Wall Cylinder Press or Shrink Fits Equations and Calculator account for the effects of shrink fits by including the interference fit between the cylinder and the shaft or hub in the calculations. The interference fit is the difference between the diameter of the shaft or hub and the diameter of the cylinder, and it can cause additional stresses on the cylinder. The calculator takes into account the friction between the cylinder and the shaft or hub, as well as the thermal expansion of the materials, which can affect the fit and the stresses on the cylinder. By including these factors in the calculations, the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator can provide a more accurate and comprehensive analysis of the stress and strain on the cylinder. This is particularly important in mechanical engineering applications, where shrink fits are commonly used to attach or secure parts together.
What are the key assumptions and limitations of the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator?
The Thick Wall Cylinder Press or Shrink Fits Equations and Calculator are based on several key assumptions and limitations. One of the main assumptions is that the material is isotropic and homogeneous, meaning that its properties are the same in all directions and locations. The calculator also assumes that the cylinder is long compared to its diameter, and that the loads are axisymmetric, meaning that they are symmetric about the axis of the cylinder. Additionally, the calculator assumes that the stress and strain on the cylinder are within the elastic range, meaning that the material is not plastic or yielding. The limitations of the calculator include its inability to account for non-linear effects, such as plasticity or creep, and its assumption of a constant temperature and environment. By understanding these assumptions and limitations, engineers can use the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator with confidence and accuracy.
How can the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator be used in real-world engineering applications?
The Thick Wall Cylinder Press or Shrink Fits Equations and Calculator can be used in a variety of real-world engineering applications, including the design and analysis of pressure vessels, pipes, turbines, and other cylindrical structures. For example, in the petroleum industry, the calculator can be used to design and analyze pipes and tubing that are subjected to high pressures and temperatures. In the aerospace industry, the calculator can be used to design and analyze rocket motors and turbines that are subjected to high stresses and loads. The calculator can also be used in the automotive industry to design and analyze engine blocks and cylinders that are subjected to high pressures and temperatures. By using the Thick Wall Cylinder Press or Shrink Fits Equations and Calculator, engineers can ensure that their designs are safe, reliable, and efficient, and that they meet the required standards and regulations. The calculator can also be used to optimize designs, reduce costs, and improve performance.
Deja una respuesta

Entradas Relacionadas