Parallelogram Section Properties Equation and Calculator

A parallelogram is a quadrilateral with opposite sides that are parallel to each other. The section properties of a parallelogram are crucial in various engineering and mathematical applications. This article provides an overview of the equation and calculator for parallelogram section properties, including area, perimeter, and diagonal lengths. The equation for these properties is derived from the geometry of the shape, allowing for precise calculations. Understanding these properties is essential for solving problems involving parallelograms in fields like architecture, physics, and mathematics. Calculator tools simplify the process, making it easier to apply these concepts in real-world scenarios.
- Parallelogram Section Properties Equation and Calculator
- What are the 7 properties of a parallelogram?
- What is the moment of inertia of a parallelogram?
- How do you find the size of a parallelogram?
-
Frequently Asked Questions (FAQs)
- What are the key properties of a parallelogram that are used in the equation and calculator for section properties?
- How is the equation for the section properties of a parallelogram derived, and what are the underlying assumptions?
- What are some of the common applications of the parallelogram section properties equation and calculator in engineering and design?
- How can the results from the parallelogram section properties equation and calculator be used to inform design decisions and optimize performance?
Parallelogram Section Properties Equation and Calculator
The Parallelogram Section Properties Equation and Calculator is a mathematical tool used to calculate the properties of a parallelogram, such as its area, perimeter, and diagonals. This tool is useful for engineers, architects, and designers who need to calculate the properties of parallelograms in their designs. The equation for the area of a parallelogram is A = b h, where A is the area, b is the base, and h is the height. The perimeter of a parallelogram is calculated using the equation P = 2 (a + b), where P is the perimeter, a is the length of one side, and b is the length of the other side.
Introduction to Parallelogram Section Properties
The Parallelogram Section Properties is a mathematical concept that deals with the calculation of the properties of a parallelogram. A parallelogram is a quadrilateral with opposite sides that are parallel to each other. The properties of a parallelogram include its area, perimeter, diagonals, and angles. The Area of a parallelogram is calculated using the equation A = b h, where A is the area, b is the base, and h is the height. The Perimeter of a parallelogram is calculated using the equation P = 2 (a + b), where P is the perimeter, a is the length of one side, and b is the length of the other side.
Parallelogram Section Properties Equation
The Parallelogram Section Properties Equation is a mathematical equation that is used to calculate the properties of a parallelogram. The equation for the area of a parallelogram is A = b h, where A is the area, b is the base, and h is the height. The equation for the perimeter of a parallelogram is P = 2 (a + b), where P is the perimeter, a is the length of one side, and b is the length of the other side. The equation for the diagonal of a parallelogram is d = sqrt(a^2 + b^2), where d is the diagonal, a is the length of one side, and b is the length of the other side.
Parallelogram Section Properties Calculator
The Parallelogram Section Properties Calculator is a mathematical tool that is used to calculate the properties of a parallelogram. This calculator uses the equations for the area, perimeter, and diagonals of a parallelogram to calculate the properties of the parallelogram. The calculator requires the user to input the values of the base and height of the parallelogram, and then calculates the area, perimeter, and diagonals of the parallelogram. The calculator also provides the user with the option to calculate the properties of the parallelogram using different units, such as inches, feet, yards, and meters.
Table of Parallelogram Section Properties
| Property | Equation | Units |
|---|---|---|
| Area | A = b h | square inches, square feet, square yards, square meters |
| Perimeter | P = 2 (a + b) | inches, feet, yards, meters |
| Diagonal | d = sqrt(a^2 + b^2) | inches, feet, yards, meters |
Applications of Parallelogram Section Properties
The Parallelogram Section Properties has a wide range of applications in engineering, architecture, and design. The properties of a parallelogram are used to calculate the area, perimeter, and diagonals of a parallelogram, which is useful in designing buildings, bridges, and other structures. The properties of a parallelogram are also used in engineering to calculate the stress and strain on a structure, which is important in designing safe and stable structures. Additionally, the properties of a parallelogram are used in design to calculate the volume and surface area of a parallelogram, which is useful in designing packages and other products.
What are the 7 properties of a parallelogram?
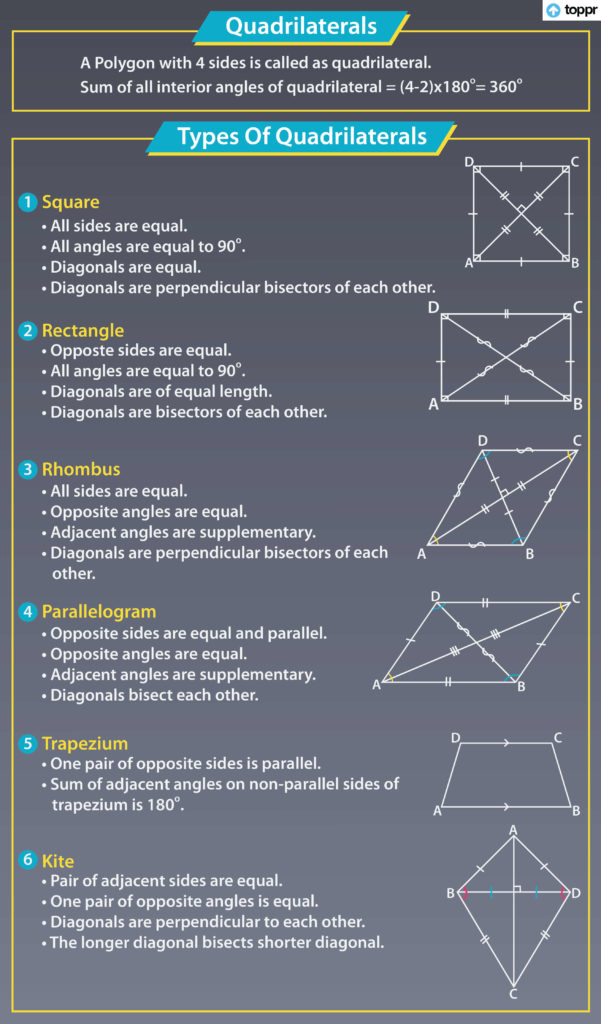
The 7 properties of a parallelogram are:
1. Opposite sides are equal in length.
2. Opposite angles are equal in measure.
3. Adjacent angles are supplementary, meaning they add up to 180 degrees.
4. Opposite sides are parallel to each other.
5. The diagonals of a parallelogram bisect each other.
6. The area of a parallelogram can be found using the formula A = base × height.
7. The perimeter of a parallelogram is the sum of the lengths of all its sides.
Properties of Opposite Sides in a Parallelogram
In a parallelogram, the opposite sides are equal in length, which means that if one pair of opposite sides has a length of 'a' units, the other pair of opposite sides will also have a length of 'a' units. Some key points about opposite sides are:
- The length of opposite sides is the same.
- Parallel lines are formed by opposite sides.
- The midpoint of opposite sides coincides when joined.
Properties of Opposite Angles in a Parallelogram
The opposite angles in a parallelogram are equal in measure, which means that if one angle is 60 degrees, the opposite angle will also be 60 degrees. Some key points about opposite angles are:
- The measure of opposite angles is the same.
- Vertical angles formed by opposite angles are also equal.
- Corresponding angles formed by a transversal are also equal.
Properties of Diagonals in a Parallelogram
The diagonals of a parallelogram bisect each other, meaning that they cut each other into two equal halves. Some key points about diagonals are:
- Bisecting each other, forming two equal parts.
- Intersecting at their midpoints.
- Dividing the parallelogram into four triangles.
Properties of Area and Perimeter in a Parallelogram
The area and perimeter of a parallelogram can be found using specific formulas. The area is found using the formula A = base × height, and the perimeter is the sum of the lengths of all its sides. Some key points about area and perimeter are:
- The area is found using the formula A = base × height.
- The perimeter is the sum of the lengths of all its sides.
- Base and height are used to calculate the area.
Properties of Adjacent Angles in a Parallelogram
The adjacent angles in a parallelogram are supplementary, meaning they add up to 180 degrees. Some key points about adjacent angles are:
- Supplementary angles add up to 180 degrees.
- Adjacent angles share a common side and vertex.
- Linear pair of angles formed by adjacent angles are supplementary.
What is the moment of inertia of a parallelogram?

The moment of inertia of a parallelogram is a measure of its resistance to changes in its rotational motion. It is a quantitative measure of the distribution of the object's mass around its axis of rotation. The moment of inertia of a parallelogram depends on its mass, size, and orientation. To calculate the moment of inertia of a parallelogram, we need to know its density and the dimensions of the parallelogram.
Moment of Inertia Formula
The moment of inertia of a parallelogram can be calculated using the formula: I = (1/12) m (a^2 + b^2), where m is the mass of the parallelogram, a is the length of one side, and b is the length of the other side. Here are some key points to consider:
- The formula assumes that the parallelogram is a uniform density object.
- The moment of inertia is a scalar quantity, but it depends on the orientation of the object.
- The formula is only applicable for rigid objects, where the distance between the particles remains constant.
Properties of Moment of Inertia
The moment of inertia has several important properties that make it a useful concept in physics and engineering. Here are some key properties:
- The moment of inertia is a measure of the object's resistance to changes in its rotational motion.
- The moment of inertia depends on the distribution of the object's mass around its axis of rotation.
- The moment of inertia can be used to calculate the torque required to produce a given angular acceleration.
Moment of Inertia Units
The units of moment of inertia are typically measured in kilogram-meters squared (kgm^2) or slug-feet squared (slugft^2). Here are some key points to consider:
- The units of moment of inertia are a measure of the object's mass and size.
- The units of moment of inertia depend on the system of units used to measure the object's mass and size.
- The units of moment of inertia are important in calculating the torque and angular acceleration of an object.
Moment of Inertia Applications
The moment of inertia has many important applications in physics, engineering, and other fields. Here are some key applications:
- The moment of inertia is used to calculate the torque required to produce a given angular acceleration.
- The moment of inertia is used to design rotating systems, such as engines and gears.
- The moment of inertia is used to analyze the stability of rotating objects, such as gyroscopes and flywheels.
Moment of Inertia Calculation
The moment of inertia can be calculated using a variety of methods, including the parallel axis theorem and the perpendicular axis theorem. Here are some key points to consider:
- The moment of inertia can be calculated using the density and dimensions of the object.
- The moment of inertia can be calculated using the mass and radius of the object.
- The moment of inertia can be calculated using numerical methods, such as finite element analysis.
How do you find the size of a parallelogram?

To find the size of a parallelogram, you need to calculate its area. The area of a parallelogram is calculated by multiplying the base length by the height. The base of a parallelogram is any of its sides, and the height is the perpendicular distance from the base to the opposite side. This can be represented by the formula: Area = base × height.
Understanding Parallelogram Properties
To calculate the size of a parallelogram, it is essential to understand its properties. A parallelogram is a quadrilateral with opposite sides that are equal and parallel. The area of a parallelogram can be found using the formula: Area = base × height. This involves identifying the base and the height of the parallelogram.
- The base can be any side of the parallelogram.
- The height is the perpendicular distance from the base to the opposite side.
- The area is calculated by multiplying the base by the height.
Calculating the Area of a Parallelogram
The area of a parallelogram can be calculated using the formula: Area = base × height. This involves identifying the base and the height of the parallelogram and then multiplying these two values together.
- Identify the base length of the parallelogram.
- Identify the height of the parallelogram, which is the perpendicular distance from the base to the opposite side.
- Multiply the base by the height to find the area.
Using the Formula for the Area of a Parallelogram
The formula for the area of a parallelogram is Area = base × height. This formula requires knowing the base length and the height of the parallelogram.
- Measure or identify the base length of the parallelogram.
- Determine the height of the parallelogram, which is the perpendicular distance from the base to the opposite side.
- Apply the formula: Area = base × height to calculate the area.
Real-World Applications of Parallelogram Area Calculation
Calculating the area of a parallelogram has real-world applications in various fields, including architecture, engineering, and design.
- In architecture, the area of a parallelogram can be used to calculate the size of walls, floors, and roofs.
- In engineering, the area of a parallelogram is used to calculate stress and load on structures.
- In design, the area of a parallelogram is used to create balanced and aesthetically pleasing compositions.
Common Mistakes in Calculating Parallelogram Area
There are common mistakes that can be made when calculating the area of a parallelogram, including using the wrong base or height.
- Using a non-perpendicular height can result in an incorrect calculation.
- Not identifying the correct base can also lead to an incorrect calculation.
- Not applying the formula correctly can result in an incorrect area.
Frequently Asked Questions (FAQs)
What are the key properties of a parallelogram that are used in the equation and calculator for section properties?
The parallelogram section properties equation and calculator are based on several key properties of a parallelogram, including its base length, height, and angle of inclination. These properties are used to calculate various section properties, such as the area, perimeter, and moments of inertia. The base length and height of a parallelogram are used to calculate its area, which is given by the formula A = bh, where A is the area, b is the base length, and h is the height. The angle of inclination is used to calculate the moments of inertia, which are measures of the resistance of the parallelogram to bending and torsion.
How is the equation for the section properties of a parallelogram derived, and what are the underlying assumptions?
The equation for the section properties of a parallelogram is derived using geometric principles and mathematical formulas. The underlying assumptions include the definition of a parallelogram as a quadrilateral with opposite sides that are parallel and equal in length. The equation is also based on the concept of similar triangles, which allows for the calculation of proportional lengths and areas. Additionally, the equation assumes that the parallelogram is a rigid body, meaning that it does not deform or change shape under external loads. The derivation of the equation involves the use of integral calculus and vector mechanics, which provide a mathematical framework for calculating the section properties.
What are some of the common applications of the parallelogram section properties equation and calculator in engineering and design?
The parallelogram section properties equation and calculator have a wide range of applications in engineering and design, including the design of structural members, such as beams and columns, and the analysis of mechanical systems, such as linkages and gears. The equation and calculator can be used to calculate the stress and strain on a structural member, as well as its buckling load and vibrational frequency. Additionally, the equation and calculator can be used to optimize the design of a mechanical system, by minimizing its weight and cost while maximizing its performance and efficiency. The equation and calculator are also used in architectural design, to calculate the loads and stresses on buildings and bridges, and to ensure their structural integrity.
How can the results from the parallelogram section properties equation and calculator be used to inform design decisions and optimize performance?
The results from the parallelogram section properties equation and calculator can be used to inform design decisions and optimize performance by providing a quantitative understanding of the behavior of a structural member or mechanical system. The results can be used to identify potential failure modes, such as buckling or yielding, and to design mitigation strategies to prevent or minimize these failures. The results can also be used to optimize the geometry and material properties of a structural member or mechanical system, to minimize its weight and cost while maximizing its performance and efficiency. Additionally, the results can be used to validate and verify the performance of a design, by comparing the predicted behavior with experimental data or field measurements. By using the results from the parallelogram section properties equation and calculator, designers and engineers can create more efficient, more reliable, and more cost-effective designs that meet or exceed performance requirements.
Deja una respuesta

Entradas Relacionadas