Linear Thermal Expansion Equation and Calculator
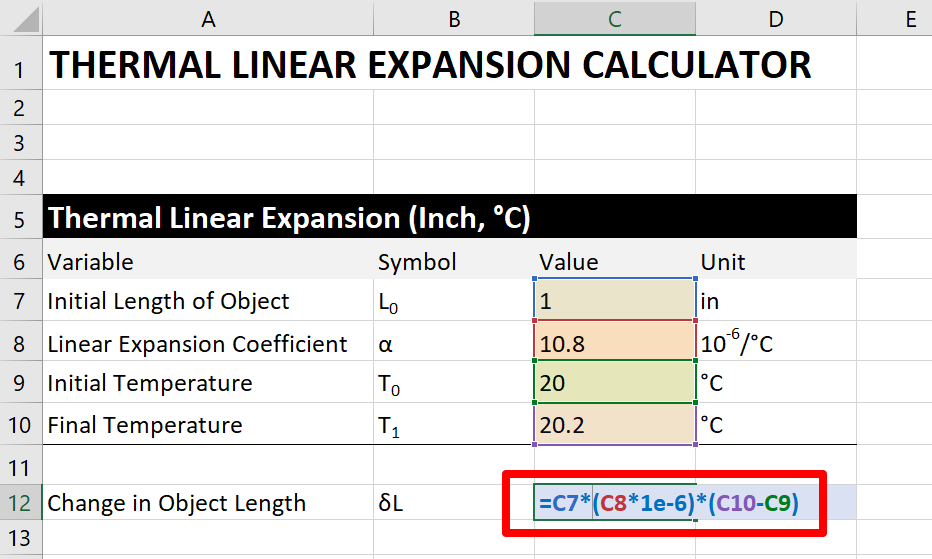
The linear thermal expansion equation is a fundamental concept in physics and engineering, describing how materials change in size when exposed to temperature variations. This equation is crucial in designing and analyzing systems that operate under different thermal conditions. The linear thermal expansion calculator is a tool that helps calculate the change in length of a material due to temperature changes, using the material's coefficient of thermal expansion. This article will explore the linear thermal expansion equation, its application, and provide a calculator to simplify the calculation process for various materials and temperature ranges.
Linear Thermal Expansion Equation and Calculator
The linear thermal expansion equation is a fundamental concept in physics and engineering, describing how materials change in size due to temperature variations. It is essential to understand and calculate this expansion to design and build structures, machines, and devices that can withstand temperature fluctuations. The linear thermal expansion equation is given by ΔL = α L ΔT, where ΔL is the change in length, α is the thermal expansion coefficient, L is the original length, and ΔT is the change in temperature.
Introduction to Thermal Expansion
Thermal expansion is the tendency of materials to expand or contract when their temperature changes. This phenomenon occurs due to the increase or decrease in the kinetic energy of the particles that make up the material. As the temperature increases, the particles gain energy and start moving more, causing the material to expand. Conversely, when the temperature decreases, the particles lose energy and move less, leading to a contraction.
Linear Thermal Expansion Equation Derivation
The linear thermal expansion equation can be derived from the definition of thermal expansion. It is assumed that the material is homogeneous and isotropic, meaning its properties are the same in all directions. The equation is derived by considering a small change in temperature and calculating the resulting change in length. The thermal expansion coefficient (α) is a measure of how much a material expands per unit change in temperature.
Thermal Expansion Coefficient Values
The thermal expansion coefficient values vary depending on the material. Some materials, like metals, have a high thermal expansion coefficient, while others, like ceramics, have a low coefficient. The values of α are typically measured experimentally and can be found in tables or online resources. For example, the thermal expansion coefficient of aluminum is around 23 × 10^(-6) K^(-1), while that of glass is around 8 × 10^(-6) K^(-1).
| Material | Thermal Expansion Coefficient (α) |
|---|---|
| Aluminum | 23 × 10^(-6) K^(-1) |
| Glass | 8 × 10^(-6) K^(-1) |
| Copper | 17 × 10^(-6) K^(-1) |
| Steel | 12 × 10^(-6) K^(-1) |
Calculating Linear Thermal Expansion
To calculate the linear thermal expansion, the equation ΔL = α L ΔT can be used. For example, if a steel rod with a length of 1 meter is heated from 20°C to 100°C, the change in length can be calculated using the thermal expansion coefficient of steel (12 × 10^(-6) K^(-1)). The change in temperature (ΔT) is 80°C, and the original length (L) is 1 meter. Plugging in these values, the change in length (ΔL) can be calculated.
Applications of Linear Thermal Expansion
The concept of linear thermal expansion has numerous practical applications in various fields, including engineering, architecture, and materials science. It is crucial to consider thermal expansion when designing structures, such as bridges, buildings, and machines, to ensure they can withstand temperature fluctuations. Additionally, understanding thermal expansion is essential in the development of sensors, actuators, and other devices that rely on precise temperature control. Engineers and researchers use the linear thermal expansion equation to predict and mitigate the effects of thermal expansion on materials and structures.
How do you calculate linear thermal expansion?

To calculate linear thermal expansion, you need to understand the concept of thermal expansion and how it affects the dimensions of a material. Linear thermal expansion refers to the change in length of a material when it is heated or cooled. The calculation involves using the coefficient of linear thermal expansion, which is a material property that describes how much a material expands or contracts per unit change in temperature.
Understanding the Coefficient of Linear Thermal Expansion
The coefficient of linear thermal expansion is a crucial factor in calculating linear thermal expansion. It is typically denoted by the symbol α (alpha) and is measured in units of 1/°C or 1/K. The coefficient of linear thermal expansion is a material property that can be found in tables or measured experimentally. To calculate linear thermal expansion, you need to know the coefficient of linear thermal expansion, the initial length of the material, and the change in temperature. Here are the steps:
- Identify the coefficient of linear thermal expansion (α) for the material.
- Measure the initial length (L0) of the material.
- Calculate the change in temperature (ΔT) to which the material is subjected.
Calculating Linear Thermal Expansion
The linear thermal expansion can be calculated using the formula: ΔL = α L0 ΔT, where ΔL is the change in length, α is the coefficient of linear thermal expansion, L0 is the initial length, and ΔT is the change in temperature. This formula allows you to calculate the new length of the material after it has been heated or cooled. For example, if you have a steel rod with an initial length of 1 meter, a coefficient of linear thermal expansion of 12 × 10^(-6) 1/°C, and it is heated from 20°C to 100°C, you can calculate the new length using the formula.
- Plug in the values into the formula: ΔL = α L0 ΔT.
- Calculate the change in length: ΔL = 12 × 10^(-6) 1/°C 1 m 80°C.
- Evaluate the result to find the new length of the steel rod.
Factors Affecting Linear Thermal Expansion
Several factors can affect the linear thermal expansion of a material, including the material's composition, crystal structure, and temperature range. The coefficient of linear thermal expansion can vary depending on the material's composition and crystal structure. Additionally, some materials may exhibit non-linear thermal expansion behavior, where the coefficient of linear thermal expansion changes with temperature. Understanding these factors is crucial for accurate calculations.
- Consider the material's composition and its effect on the coefficient of linear thermal expansion.
- Examine the crystal structure of the material and its influence on thermal expansion.
- Evaluate the temperature range over which the material will be used.
Applications of Linear Thermal Expansion Calculations
Accurate calculations of linear thermal expansion are essential in various engineering applications, such as designing mechanical systems, building construction, and manufacturing processes. By understanding how materials expand and contract with temperature changes, engineers can design systems that can withstand thermal stresses and ensure safe operation. For example, in high-temperature applications, such as gas turbines or heat exchangers, accurate calculations of linear thermal expansion are critical to prevent thermal fatigue and failure.
- Apply linear thermal expansion calculations to design mechanical systems that can withstand thermal stresses.
- Use thermal expansion calculations in building construction to ensure structural integrity.
- Integrate linear thermal expansion considerations into manufacturing processes to optimize product performance.
Common Mistakes in Linear Thermal Expansion Calculations
When calculating linear thermal expansion, it is essential to avoid common mistakes, such as ignoring the temperature dependence of the coefficient of linear thermal expansion or using incorrect units. Additionally, assuming a constant coefficient of linear thermal expansion over a wide temperature range can lead to inaccurate results. To ensure accurate calculations, it is crucial to carefully evaluate the material properties, temperature range, and units used in the calculation.
- Avoid ignoring the temperature dependence of the coefficient of linear thermal expansion.
- Use correct units for the coefficient of linear thermal expansion and other parameters.
- Evaluate the material properties carefully to ensure accurate calculations.
How do you calculate the thermal expansion of stainless steel?

To calculate the thermal expansion of stainless steel, you need to consider the coefficient of thermal expansion, which is a measure of how much the material expands when it is heated. This coefficient is usually expressed in units of length per unit length per degree Celsius (m/m°C) or length per unit length per degree Fahrenheit (m/m°F). The calculation involves multiplying the coefficient of thermal expansion by the change in temperature and the original length of the material.
Understanding Thermal Expansion Coefficients
The coefficient of thermal expansion is a critical factor in calculating the thermal expansion of stainless steel. This coefficient varies depending on the type of stainless steel alloy and its composition. For example, Austenitic stainless steel alloys like 304 and 316 have a higher coefficient of thermal expansion compared to Ferritic stainless steel alloys like 430. To calculate the thermal expansion, you need to look up the coefficient of thermal expansion for the specific stainless steel alloy you are working with.
- Identify the type of stainless steel alloy and its composition
- Look up the coefficient of thermal expansion for the specific stainless steel alloy
- Multiply the coefficient of thermal expansion by the change in temperature and the original length of the material
Factors Affecting Thermal Expansion
Several factors can affect the thermal expansion of stainless steel, including the type of stainless steel alloy, the temperature range, and the presence of any stresses or constraints. For example, stainless steel alloys with a higher nickel content tend to have a higher coefficient of thermal expansion. Additionally, the thermal expansion of stainless steel can be affected by the presence of any welds or joints, which can create stress concentrations that can lead to distortion or cracking.
- Consider the type of stainless steel alloy and its composition
- Evaluate the temperature range and any potential stresses or constraints
- Assess the presence of any welds or joints and their potential impact on thermal expansion
Calculating Thermal Expansion
To calculate the thermal expansion of stainless steel, you can use the following formula: ΔL = α L ΔT, where ΔL is the change in length, α is the coefficient of thermal expansion, L is the original length, and ΔT is the change in temperature. This formula can be used to calculate the thermal expansion of stainless steel over a specific temperature range.
- Identify the original length of the stainless steel material
- Determine the change in temperature (ΔT)
- Multiply the coefficient of thermal expansion by the change in temperature and the original length
Measuring Thermal Expansion
Measuring the thermal expansion of stainless steel can be done using a variety of techniques, including dilatometry and thermomechanical analysis. These techniques involve measuring the change in length of the stainless steel material as it is heated or cooled.
- Choose a suitable measurement technique, such as dilatometry or thermomechanical analysis
- Prepare the stainless steel sample for measurement
- Measure the change in length of the stainless steel material over a specific temperature range
Applications of Thermal Expansion Calculations
Calculating the thermal expansion of stainless steel is important in a variety of applications, including engineering design, materials science, and research and development. For example, thermal expansion calculations can be used to design heat exchangers, pipelines, and other equipment that must withstand high temperatures.
- Identify the specific application and its requirements
- Calculate the thermal expansion of the stainless steel material
- Use the calculated thermal expansion to inform the design or selection of materials and equipment
What is the thermal expansion of steel beam?

The thermal expansion of a steel beam refers to the change in its length or size due to a change in temperature. This phenomenon occurs because steel, like most materials, expands when heated and contracts when cooled. The thermal expansion coefficient of steel is typically around 12 × 10^-6 per degree Celsius, meaning that for every degree Celsius change in temperature, the steel beam will expand or contract by 12 × 10^-6 times its original length.
Introduction to Thermal Expansion
Thermal expansion is a critical factor to consider in the design and construction of steel structures, as it can affect the stability and integrity of the building or bridge. The thermal expansion of steel beams can be significant, especially in large structures or those exposed to extreme temperature fluctuations. To mitigate the effects of thermal expansion, engineers use various techniques, such as:
- Using expansion joints to allow for movement between sections of the structure
- Designing the structure to accommodate thermal expansion, such as using sliding connections or flexible supports
- Selecting materials with low thermal expansion coefficients, such as certain types of steel alloys
Factors Affecting Thermal Expansion
Several factors can influence the thermal expansion of steel beams, including the temperature range, material properties, and structural design. The temperature range is a critical factor, as it determines the amount of thermal expansion that will occur. Other factors, such as the modulus of elasticity and Poisson's ratio, can also affect the thermal expansion of steel beams. Some key factors to consider are:
- Temperature differences between the steel beam and its surroundings
- Humidity levels, which can affect the corrosion and durability of the steel
- Support conditions, such as the type and quality of anchors or fasteners
Measuring Thermal Expansion
To measure the thermal expansion of a steel beam, engineers typically use sensors or transducers to monitor changes in the beam's length or strain. Some common methods for measuring thermal expansion include:
- Using strain gauges to measure changes in the beam's strain
- Employing laser interferometry to measure changes in the beam's length
- Utilizing thermocouples to measure temperature changes in the beam
Designing for Thermal Expansion
When designing steel structures, engineers must consider the potential effects of thermal expansion on the stability and safety of the building or bridge. To design for thermal expansion, engineers can use various techniques, such as:
- Using finite element analysis to model the behavior of the steel structure under different temperature conditions
- Conducting thermal analysis to determine the temperature distribution within the structure
- Selecting materials and designs that can accommodate thermal expansion, such as flexible connections or movable supports
Applications and Examples
Thermal expansion is a critical consideration in a wide range of applications, from building design to bridge construction. Some examples of how thermal expansion can affect steel structures include:
- High-rise buildings, where thermal expansion can cause significant movements in the structure
- Long-span bridges, where thermal expansion can affect the alignment and stability of the bridge
- Industrial equipment, such as pipelines or tanks, where thermal expansion can impact the performance and safety of the system
Frequently Asked Questions (FAQs)
What is the Linear Thermal Expansion Equation and how is it used?
The Linear Thermal Expansion Equation is a mathematical formula used to calculate the change in length of a material due to a change in temperature. This equation is commonly used in engineering and physics to predict the behavior of materials under different thermal conditions. The equation is given by ΔL = αL₀ΔT, where ΔL is the change in length, α is the coefficient of thermal expansion, L₀ is the initial length, and ΔT is the change in temperature. This equation is fundamental in understanding how materials respond to temperature changes and is used in a wide range of applications, from designing buildings and bridges to manufacturing electronic components.
How does the Linear Thermal Expansion Calculator work?
The Linear Thermal Expansion Calculator is an online tool that uses the Linear Thermal Expansion Equation to calculate the change in length of a material. The calculator requires the user to input the initial length of the material, the change in temperature, and the coefficient of thermal expansion. The calculator then uses these values to calculate the change in length and displays the result. The calculator is user-friendly and allows users to easily calculate the thermal expansion of different materials, making it a valuable tool for engineers, physicists, and researchers. The calculator can also be used to calculate the coefficient of thermal expansion if the change in length and temperature are known.
What are the limitations of the Linear Thermal Expansion Equation?
The Linear Thermal Expansion Equation assumes that the material is homogeneous and isotropic, meaning that its properties are the same in all directions. However, in reality, many materials are anisotropic, meaning that their properties vary depending on the direction. Additionally, the equation assumes that the temperature change is uniform, which may not always be the case. The equation also assumes that the material is elastic, meaning that it returns to its original shape after the temperature change. However, some materials may undergo plastic deformation, which is not accounted for by the equation. Despite these limitations, the Linear Thermal Expansion Equation is still a powerful tool for predicting the thermal expansion of materials and is widely used in many fields.
How can I use the Linear Thermal Expansion Equation in real-world applications?
The Linear Thermal Expansion Equation has a wide range of practical applications in many fields, including engineering, physics, and materials science. For example, in civil engineering, the equation is used to design bridges and buildings that can withstand temperature changes. In mechanical engineering, the equation is used to design engines and machinery that can operate in high-temperature environments. In electrical engineering, the equation is used to design electronic components that can withstand temperature changes. The equation is also used in materials science to study the properties of new materials and to develop new technologies. By understanding how to apply the Linear Thermal Expansion Equation, engineers and researchers can design and develop innovative solutions to real-world problems.
Deja una respuesta

Entradas Relacionadas