Horizontal Tank Draining Time Formulas and Calculator

Calculating the time it takes to drain a horizontal tank is crucial in various industrial applications, including chemical processing, oil and gas, and water treatment. The draining time depends on several factors, such as the tank's dimensions, fluid properties, and outlet conditions. To simplify this complex calculation, formulas and calculators have been developed, providing engineers and operators with a reliable tool to estimate the time required to empty a horizontal tank. This article presents the formulas and a calculator for determining horizontal tank draining time.
-
Calculating Horizontal Tank Draining Time with Formulas and Calculator
- Introduction to Horizontal Tank Draining Time Formulas
- Understanding the Horizontal Tank Draining Time Calculator
- Factors Affecting Horizontal Tank Draining Time
- Applications of Horizontal Tank Draining Time Formulas and Calculator
- Benefits of Using Horizontal Tank Draining Time Formulas and Calculator
- How do you calculate time to empty a tank?
- What is the formula for draining a tank?
- What is the formula for the volume of a horizontal elliptical tank?
- What is the formula for the volume of water in a horizontal cylindrical tank?
-
Frequently Asked Questions (FAQs)
- What are the key factors that affect the horizontal tank draining time?
- How do I calculate the draining time of a horizontal tank using formulas?
- What are the advantages of using a horizontal tank draining time calculator?
- How can I apply the horizontal tank draining time formulas and calculator in real-world applications?
Calculating Horizontal Tank Draining Time with Formulas and Calculator
Calculating the draining time of a horizontal tank is crucial in various industries, including petroleum, chemical, and water treatment. The draining time depends on several factors, including the tank's dimensions, fluid properties, and drainage system. To calculate the draining time, several formulas and calculators are used, taking into account the torispherical head and elliptical head of the tank. These formulas and calculators provide accurate estimates of the draining time, ensuring efficient and safe operations.
Introduction to Horizontal Tank Draining Time Formulas
The draining time of a horizontal tank can be calculated using various formulas, including the torispherical head and elliptical head formulas. These formulas take into account the tank's dimensions, fluid properties, and drainage system. The torispherical head formula is used for tanks with a torispherical head, while the elliptical head formula is used for tanks with an elliptical head. The formulas provide accurate estimates of the draining time, ensuring efficient and safe operations.
Understanding the Horizontal Tank Draining Time Calculator
The horizontal tank draining time calculator is a tool used to calculate the draining time of a horizontal tank. The calculator takes into account the tank's dimensions, fluid properties, and drainage system. The calculator uses the torispherical head and elliptical head formulas to provide accurate estimates of the draining time. The calculator is user-friendly and provides quick and accurate results, making it an essential tool in various industries.
Factors Affecting Horizontal Tank Draining Time
Several factors affect the draining time of a horizontal tank, including the tank's dimensions, fluid properties, and drainage system. The tank's dimensions, such as the length, diameter, and height, play a crucial role in determining the draining time. The fluid properties, such as the viscosity and density, also affect the draining time. The drainage system, including the pipe size and valve type, also impacts the draining time. Understanding these factors is essential to calculate the draining time accurately.
Applications of Horizontal Tank Draining Time Formulas and Calculator
The horizontal tank draining time formulas and calculator have various applications in industries such as petroleum, chemical, and water treatment. The formulas and calculator are used to calculate the draining time of storage tanks, process tanks, and wast!e tanks. The formulas and calculator provide accurate estimates of the draining time, ensuring efficient and safe operations. The formulas and calculator are also used to design and optimize drainage systems, reducing costs and environmental impacts.
Benefits of Using Horizontal Tank Draining Time Formulas and Calculator
Using the horizontal tank draining time formulas and calculator provides several benefits, including accurate estimates of the draining time, efficient and safe operations, and cost savings. The formulas and calculator also help to optimize drainage systems, reducing environmental impacts. The formulas and calculator are user-friendly and provide quick results, making them an essential tool in various industries. The formulas and calculator also help to reduce the risk of accidents and spills, ensuring a safe working environment.
| Tank Type | Draining Time Formula | Calculator |
|---|---|---|
| Torispherical Head Tank | torispherical head formula | torispherical head calculator |
| Elliptical Head Tank | elliptical head formula |
How do you calculate time to empty a tank?

To calculate the time to empty a tank, you need to know the volume of the tank and the flow rate of the liquid being drained. The formula to calculate the time to empty a tank is: time = volume / flow rate. For example, if you have a tank with a volume of 1000 gallons and a flow rate of 10 gallons per minute, the time to empty the tank would be 100 minutes.
Understanding Tank Volume
The volume of a tank is typically measured in units such as gallons or liters. To calculate the volume of a tank, you need to know the dimensions of the tank, including its length, width, and height. The formula to calculate the volume of a tank is: volume = length x width x height. For example, if you have a tank with a length of 10 feet, a width of 5 feet, and a height of 6 feet, the volume of the tank would be:
- Calculate the area of the base of the tank: area = length x width = 10 x 5 = 50 square feet
- Calculate the volume of the tank: volume = area x height = 50 x 6 = 300 cubic feet
- Convert the volume to gallons: 1 cubic foot = 7.48 gallons, so volume = 300 x 7.48 = 2244 gallons
Calculating Flow Rate
The flow rate of a liquid being drained from a tank is typically measured in units such as gallons per minute (gpm) or liters per second (L/s). To calculate the flow rate, you need to know the pressure and viscosity of the liquid, as well as the diameter and length of the pipe or valve through which the liquid is flowing. The formula to calculate the flow rate is: flow rate = (pressure x diameter^2) / (viscosity x length). For example, if you have a pipe with a diameter of 2 inches and a length of 10 feet, and the liquid has a pressure of 10 psi and a viscosity of 1 cP, the flow rate would be:
- Calculate the pressure in units of pounds per square inch: pressure = 10 psi
- Calculate the diameter in units of inches: diameter = 2 inches
- Calculate the length in units of feet: length = 10 feet
Factors Affecting Time to Empty
There are several factors that can affect the time to empty a tank, including the shape and size of the tank, the type and viscosity of the liquid, and the pressure and flow rate of the liquid being drained. For example, a tank with a narrow shape may take longer to empty than a tank with a wide shape, due to the restricted flow rate. Additionally, a liquid with a high viscosity may take longer to empty than a liquid with a low viscosity, due to the increased resistance to flow. The factors that affect the time to empty a tank are:
- Tank shape and size: the shape and size of the tank can affect the flow rate and pressure of the liquid being drained
- Liquid type and viscosity: the type and viscosity of the liquid can affect the flow rate and pressure of the liquid being drained
- Pressure and flow rate: the pressure and flow rate of the liquid being drained can affect the time to empty the tank
Using the Formula to Calculate Time to Empty
To use the formula to calculate the time to empty a tank, you need to know the volume of the tank and the flow rate of the liquid being drained. The formula is: time = volume / flow rate. For example, if you have a tank with a volume of 1000 gallons and a flow rate of 10 gallons per minute, the time to empty the tank would be:
- Calculate the volume of the tank: volume = 1000 gallons
- Calculate the flow rate of the liquid being drained: flow rate = 10 gallons per minute
- Calculate the time to empty the tank: time = volume / flow rate = 1000 / 10 = 100 minutes
Applications of Time to Empty Calculations
The calculation of the time to empty a tank has several practical applications, including designing and operating storage tanks, predicting and preventing spills, and optimizing and managing liquid handling systems. For example, a chemical plant may use the calculation to determine the time it takes to empty a tank of hazardous material, in order to predict and prevent potential spills. The applications of time to empty calculations are:
- Designing and operating storage tanks: the calculation can be used to design and operate storage tanks, including sizing and configuring the tank and selecting and installing the necessary pumps and valves
- Predicting and preventing spills: the calculation can be used to predict and prevent potential spills, including calculating the time it takes to empty a tank and identifying potential leaks and weaknesses
- Optimizing and managing liquid handling systems: the calculation can be used to optimize and manage liquid handling systems, including sizing and configuring the system and selecting and installing the necessary pumps and valves
What is the formula for draining a tank?

The formula for draining a tank is based on the principle of torricelli's theorem, which states that the velocity of fluid flowing out of a small hole in a tank is proportional to the square root of the height of the fluid above the hole. The formula is given by:
Q = A sqrt(2 g h)
Where:
Q = volumetric flow rate
A = cross-sectional area of the hole
g = acceleration due to gravity
h = height of the fluid above the hole
Understanding the Variables
The variables in the formula are crucial in determining the draining rate of the tank. The cross-sectional area of the hole affects the amount of fluid that can flow out, while the height of the fluid above the hole determines the pressure driving the flow. The acceleration due to gravity is a constant that affects the velocity of the fluid.
- The volumetric flow rate is the volume of fluid flowing out of the tank per unit time.
- The cross-sectional area of the hole is the area through which the fluid flows out.
- The height of the fluid above the hole is the vertical distance from the surface of the fluid to the hole.
Factors Affecting Draining Rate
Several factors can affect the draining rate of a tank, including the size and shape of the hole, the viscosity of the fluid, and the pressure at the bottom of the tank.
- The size of the hole affects the amount of fluid that can flow out.
- The shape of the hole can affect the flow pattern and the velocity of the fluid.
- The viscosity of the fluid affects its resistance to flow.
Applications of the Formula
The formula for draining a tank has several practical applications, including designing drainage systems for tanks and reservoirs, and predicting the draining time for a tank.
- The formula can be used to design drainage systems for tanks and reservoirs.
- The formula can be used to predict the draining time for a tank.
- The formula can be used to determine the required size of a drainage hole.
Limitations of the Formula
The formula for draining a tank has several limitations, including assuming a small hole and neglecting frictional losses.
- The formula assumes a small hole, which may not be realistic in all situations.
- The formula neglects frictional losses, which can affect the draining rate.
- The formula assumes a constant pressure at the bottom of the tank.
Derivation of the Formula
The formula for draining a tank can be derived using the principles of fluid mechanics, including conservation of energy and torricelli's theorem.
- The principles of fluid mechanics can be used to derive the formula.
- The conservation of energy principle can be used to relate the potential energy of the fluid to its kinetic energy.
- The torricelli's theorem can be used to relate the velocity of the fluid to the height of the fluid above the hole.
What is the formula for the volume of a horizontal elliptical tank?
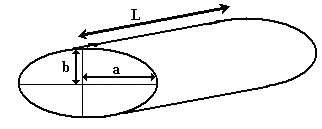
The formula for the volume of a horizontal elliptical tank is given by V = (π a b L) / 4, where a and b are the lengths of the semi-axes of the elliptical cross-section, and L is the length of the tank. This formula is used to calculate the volume of the tank, which is essential for determining the amount of fluid it can hold. The formula is derived from the geometry of the elliptical shape and the length of the tank.
Understanding the Formula
The formula for the volume of a horizontal elliptical tank is based on the principle of geometry, where the area of the elliptical cross-section is multiplied by the length of the tank. The area of the ellipse is given by A = π a b, where a and b are the lengths of the semi-axes. To calculate the volume, we multiply this area by the length of the tank and divide by 4, resulting in the formula V = (π a b L) / 4. The key elements of this formula are:
- The semi-axes of the elliptical cross-section, which are represented by a and b.
- The length of the tank, which is represented by L.
- The constant π, which is a mathematical constant approximately equal to 3.14159.
Calculating the Volume
To calculate the volume of a horizontal elliptical tank, we need to know the dimensions of the tank, including the lengths of the semi-axes and the length of the tank. We can then plug these values into the formula to get the volume. For example, if the semi-axes are 2 meters and 1 meter, and the length of the tank is 5 meters, we can calculate the volume as V = (π 2 1 5) / 4. The key steps in calculating the volume are:
- Measure the dimensions of the tank, including the lengths of the semi-axes and the length of the tank.
- Plug the values into the formula V = (π a b L) / 4.
- Perform the calculation to get the volume of the tank.
Applications of the Formula
The formula for the volume of a horizontal elliptical tank has several practical applications, including calculating the amount of fluid a tank can hold, determining the size of a tank needed for a specific application, and designing storage systems for fluids. The formula is also used in engineering and architecture to design and build tanks and other fluid storage systems. The key applications of the formula are:
- Fluid storage, where the formula is used to calculate the amount of fluid a tank can hold.
- Tank design, where the formula is used to determine the size of a tank needed for a specific application.
- Storage system design, where the formula is used to design and build storage systems for fluids.
Limitations of the Formula
The formula for the volume of a horizontal elliptical tank has several limitations, including the assumption that the tank is perfectly elliptical and that the walls of the tank are thin. In reality, tanks may have irregular shapes and thick walls, which can affect the accuracy of the formula. The key limitations of the formula are:
- The assumption of a perfectly elliptical shape, which may not be the case in reality.
- The assumption of thin walls, which may not be the case in reality.
- The potential for irregular shapes and other factors to affect the accuracy of the formula.
Real-World Examples
The formula for the volume of a horizontal elliptical tank is used in a variety of real-world applications, including oil tanks, water tanks, and chemical tanks. For example, an oil company may use the formula to calculate the amount of oil a tank can hold, while a water treatment plant may use the formula to determine the size of a tank needed for a specific application. The key examples of real-world applications are:
- Oil tanks, where the formula is used to calculate the amount of oil a tank can hold.
- Water tanks, where the formula is used to determine the size of a tank needed for a specific application.
- Chemical tanks, where the formula is used to calculate the amount of chemical a tank can hold.
What is the formula for the volume of water in a horizontal cylindrical tank?

The formula for the volume of water in a horizontal cylindrical tank is given by V = πR²L, where V is the volume of water, π is a mathematical constant approximately equal to 3.14, R is the radius of the tank, and L is the length of the tank. However, this formula only applies when the tank is completely filled with water. When the tank is partially filled, the volume of water can be calculated using the formula V = L (R² arccos(1 - h/R) - (R - h) sqrt(2 R h - h²)), where h is the height of the water in the tank.
Understanding the Formula
To understand the formula for the volume of water in a horizontal cylindrical tank, it is essential to know the dimensions of the tank, including its length, radius, and the height of the water. The formula can be broken down into several components, including the area of the circular segment of the tank that is filled with water, and the length of the tank. The formula can be applied in various situations, including:
- Calculation of water volume: The formula can be used to calculate the volume of water in a tank, which is essential for various applications, such as water storage and irrigation.
- Design of tanks: The formula can be used to design tanks with specific dimensions, such as length, radius, and height, to meet the required water storage capacity.
- Monitoring of water level: The formula can be used to monitor the water level in a tank, which is essential for maintaining the optimal water level and preventing overflow or underflow.
Applications of the Formula
The formula for the volume of water in a horizontal cylindrical tank has various applications in different fields, including engineering, architecture, and agriculture. The formula can be used to design and optimize water storage systems, such as reservoirs and irrigation systems. The formula can also be used to monitor and control the water level in tanks, which is essential for maintaining the optimal water level and preventing overflow or underflow. Some of the key applications of the formula include:
- Water storage: The formula can be used to calculate the volume of water in a tank, which is essential for water storage and irrigation.
- Irrigation systems: The formula can be used to design and optimize irrigation systems, which is essential for agriculture and horticulture.
- Reservoir design: The formula can be used to design and optimize reservoirs, which is essential for water supply and flood control.
Limitations of the Formula
The formula for the volume of water in a horizontal cylindrical tank has some limitations, including the assumption that the tank is perfectly cylindrical and that the water is perfectly still. In reality, tanks may have irregular shapes and uneven bottoms, which can affect the accuracy of the formula. Additionally, the formula does not take into account other factors that can affect the volume of water in a tank, such as evaporation and leakage. Some of the key limitations of the formula include:
- Assumptions: The formula assumes that the tank is perfectly cylindrical and that the water is perfectly still, which may not be the case in reality.
- Inaccuracies: The formula can be inaccurate if the tank has an irregular shape or an uneven bottom.
- Other factors: The formula does not take into account other factors that can affect the volume of water in a tank, such as evaporation and leakage.
Derivation of the Formula
The formula for the volume of water in a horizontal cylindrical tank can be derived using calculus and geometry. The formula can be derived by integrating the area of the circular segment of the tank that is filled with water, with respect to the length of the tank. The formula can also be derived using trigonometry and geometry, by analyzing the shape of the tank and the position of the water. Some of the key steps in deriving the formula include:
- Integration: The formula can be derived by integrating the area of the circular segment of the tank that is filled with water, with respect to the length of the tank.
- Trigonometry: The formula can be derived using trigonometry and geometry, by analyzing the shape of the tank and the position of the water.
- Geometry: The formula can be derived by analyzing the shape of the tank and the position of the water, using geometric principles.
Real-World Examples
The formula for the volume of water in a horizontal cylindrical tank has many real-world applications, including water storage, irrigation, and flood control. The formula can be used to design and optimize water storage systems, such as reservoirs and irrigation systems. The formula can also be used to monitor and control the water level in tanks, which is essential for maintaining the optimal water level and preventing overflow or underflow. Some examples of real-world applications of the formula include:
- Water supply: The formula can be used to design and optimize water storage systems, such as reservoirs and irrigation systems, to meet the water supply needs of a community.
- Flood control: The formula can be used to design and optimize flood control systems, such as dams and levees, to prevent flooding and protect communities.
- Agriculture: The formula can be used to design and optimize irrigation systems, which is essential for agriculture and horticulture.
Frequently Asked Questions (FAQs)
What are the key factors that affect the horizontal tank draining time?
The draining time of a horizontal tank is influenced by several key factors, including the tank's dimensions, fluid properties, and discharge conditions. The length, diameter, and height of the tank all play a crucial role in determining the draining time, as they affect the volume and surface area of the fluid. Additionally, the viscosity and density of the fluid, as well as the pressure and flow rate at the discharge point, also have a significant impact on the draining time. Formulas and calculators can be used to estimate the draining time based on these factors, taking into account the complex interactions between the tank's geometry, fluid properties, and discharge conditions.
How do I calculate the draining time of a horizontal tank using formulas?
To calculate the draining time of a horizontal tank, you can use formulas that take into account the tank's dimensions, fluid properties, and discharge conditions. One common formula used is the torricelli's equation, which relates the flow rate to the height and diameter of the tank, as well as the density and viscosity of the fluid. Alternatively, you can use empirical formulas or semi-empirical models that have been developed based on experimental data and theoretical analysis. These formulas and models can be used to estimate the draining time for a wide range of tank geometries and fluid properties, and can be implemented in calculators or software programs to simplify the calculation process. By using these formulas and calculators, you can quickly and accurately estimate the draining time of a horizontal tank under various operating conditions.
What are the advantages of using a horizontal tank draining time calculator?
Using a horizontal tank draining time calculator offers several advantages over manual calculations or estimations. Firstly, a calculator can quickly and accurately perform complex calculations, reducing the risk of human error and saving time. Additionally, a calculator can handle a wide range of input parameters, allowing you to easily explore different scenarios and operating conditions. Furthermore, a calculator can provide detailed output, including charts and graphs, to help you visualize and understand the draining process. This can be particularly useful for optimizing the design and operation of horizontal tanks, as well as for troubleshooting and maintenance purposes. By using a calculator, you can also validate your design and operating assumptions, and identify potential bottlenecks or areas for improvement.
How can I apply the horizontal tank draining time formulas and calculator in real-world applications?
The horizontal tank draining time formulas and calculator can be applied in a wide range of real-world applications, including chemical processing, oil and gas, water treatment, and food processing. For example, in chemical processing, the formulas and calculator can be used to design and optimize the draining system for a horizontal tank, ensuring that the fluid is drained safely and efficiently. In oil and gas, the calculator can be used to predict the draining time of a horizontal tank under different operating conditions, allowing for better planning and management of tank operations. In water treatment, the formulas and calculator can be used to design and operate horizontal tanks for water storage and treatment, ensuring that the water is drained and treated effectively. By applying the horizontal tank draining time formulas and calculator in these and other real-world applications, you can improve the efficiency, safety, and reliability of your operations.
Deja una respuesta

Entradas Relacionadas