Horizontal Cylinder Natural Convection Equation and Calculator
Natural convection in horizontal cylinders is a complex phenomenon that plays a crucial role in various engineering applications, including heat exchangers and thermal energy storage systems. The horizontal cylinder natural convection equation is a mathematical model used to predict the heat transfer rate and temperature distribution within the cylinder. This equation takes into account the physical properties of the fluid, the cylinder's dimensions, and the temperature difference between the cylinder and the surrounding environment, allowing engineers to design and optimize systems for efficient heat transfer. An online calculator can simplify this process.
- Natural Convection in Horizontal Cylinders: An In-Depth Analysis
- What is the formula for convection of a cylinder?
- What is the formula for natural convection?
- What is the formula for the Rayleigh number of a cylinder?
- What is the convection coefficient of air at 20 °C?
-
Frequently Asked Questions (FAQs)
- What is the Horizontal Cylinder Natural Convection Equation and how is it used in calculations?
- How does the Horizontal Cylinder Natural Convection Equation account for the effects of buoyancy and fluid flow?
- What are the limitations and assumptions of the Horizontal Cylinder Natural Convection Equation?
- How can the Horizontal Cylinder Natural Convection Equation be applied in engineering design and optimization?
Natural Convection in Horizontal Cylinders: An In-Depth Analysis
Natural convection in horizontal cylinders is a complex phenomenon that involves the transfer of heat through the movement of fluids. This process occurs when a horizontal cylinder is heated, causing the fluid surrounding it to expand and rise, creating a circulation of fluid. The natural convection equation is used to predict the heat transfer rate in such scenarios. The equation takes into account various factors, including the temperature difference between the cylinder and the surrounding fluid, the properties of the fluid, and the geometry of the cylinder.
Introduction to Natural Convection
Natural convection is a type of heat transfer that occurs when there is a difference in temperature between two objects or a object and its surroundings. In the case of a horizontal cylinder, natural convection occurs when the cylinder is heated, causing the surrounding fluid to expand and rise. This creates a circulation of fluid, which in turn transfers heat away from the cylinder. The natural convection coefficient is a key parameter in predicting the heat transfer rate, as it takes into account the fluid properties and the geometry of the cylinder.
Natural Convection Equation
The natural convection equation for a horizontal cylinder is given by:
Q = h A (T_s - T_f)
where Q is the heat transfer rate, h is the natural convection coefficient, A is the surface area of the cylinder, T_s is the surface temperature of the cylinder, and T_f is the temperature of the surrounding fluid. The natural convection coefficient is a function of the fluid properties, such as the thermal conductivity, viscosity, and specific heat capacity.
Calculator for Natural Convection
A calculator for natural convection in horizontal cylinders can be a useful tool for predicting the heat transfer rate. Such a calculator would typically take into account the input parameters, such as the temperature difference, fluid properties, and cylinder geometry, and output the heat transfer rate. The calculator would use the natural convection equation to perform the calculations.
Factors Affecting Natural Convection
Several factors can affect the natural convection in horizontal cylinders, including:
| Factor | Description |
|---|---|
| Temperature difference | The temperature difference between the cylinder and the surrounding fluid is a key factor in natural convection. |
| Fluid properties | The properties of the fluid, such as the thermal conductivity, viscosity, and specific heat capacity, can affect the natural convection. |
| Cylinder geometry | The geometry of the cylinder, including its diameter and length, can affect the natural convection. |
Applications of Natural Convection
Natural convection in horizontal cylinders has several applications, including:
the design of heat exchangers, chemical reactors, and electronic cooling systems. By understanding the natural convection equation and the factors that affect it, engineers can design more efficient systems that take advantage of natural convection to transfer heat.
What is the formula for convection of a cylinder?

The formula for convection of a cylinder is given by the equation: h = (k / d) Nu, where h is the convective heat transfer coefficient, k is the thermal conductivity of the fluid, d is the diameter of the cylinder, and Nu is the Nusselt number. The Nusselt number is a dimensionless quantity that depends on the Reynolds number and the Prandtl number.
Introduction to Convection of a Cylinder
The convection of a cylinder is a complex phenomenon that involves the transfer of heat from the cylinder to the surrounding fluid. The convective heat transfer coefficient is a measure of the rate at which heat is transferred from the cylinder to the fluid. The formula for convection of a cylinder takes into account the thermal conductivity of the fluid, the diameter of the cylinder, and the Nusselt number. Some key factors that affect the convection of a cylinder include:
- The velocity of the fluid flowing past the cylinder
- The temperature difference between the cylinder and the fluid
- The properties of the fluid, such as its density and viscosity
Nusselt Number for Convection of a Cylinder
The Nusselt number is a critical parameter in the formula for convection of a cylinder. It is a dimensionless quantity that depends on the Reynolds number and the Prandtl number. The Nusselt number can be calculated using empirical correlations or numerical simulations. The Nusselt number is affected by the flow regime, which can be either laminar or turbulent. Some key factors that affect the Nusselt number include:
- The Reynolds number, which characterizes the flow regime
- The Prandtl number, which characterizes the thermal properties of the fluid
- The surface roughness of the cylinder
Convective Heat Transfer Coefficient for a! Cylinder
The convective heat transfer coefficient is a measure of the rate at which heat is transferred from the cylinder to the surrounding fluid. The convective heat transfer coefficient depends on the thermal conductivity of the fluid, the diameter of the cylinder, and the Nusselt number. The convective heat transfer coefficient can be calculated using the formula: h = (k / d) Nu. Some key factors that affect the convective heat transfer coefficient include:
- The thermal conductivity of the fluid
- The diameter of the cylinder
- The Nusselt number, which depends on the Reynolds number and the Prandtl number
Reynolds Number for Convection of a Cylinder
The Reynolds number is a dimensionless quantity that characterizes the flow regime of the fluid flowing past the cylinder. The Reynolds number depends on the velocity of the fluid, the diameter of the cylinder, and the viscosity of the fluid. The Reynolds number can be used to predict the flow regime, which can be either laminar or turbulent. Some key factors that affect the Reynolds number include:
- The velocity of the fluid flowing past the cylinder
- The diameter of the cylinder
- The viscosity of the fluid
Applications of Convection of a Cylinder
The convection of a cylinder has numerous applications in various fields, including heat transfer, fluid mechanics, and thermal engineering. The convection of a cylinder is used to design and optimize heat exchangers, radiators, and cooling systems. Some key applications of the convection of a cylinder include:
- Heat exchangers, which are used to transfer heat from one fluid to another
- Radiators, which are used to cool engines and other machinery
- Cooling systems, which are used to cool electronic devices and other equipment
What is the formula for natural convection?

The formula for natural convection is given by the equation: Nu = (h L) / k, where Nu is the Nusselt number, h is the convective heat transfer coefficient, L is the characteristic length, and k is the thermal conductivity of the fluid. This formula is used to calculate the rate of heat transfer due to natural convection, which occurs when there is a temperature difference between a surface and the surrounding fluid, causing the fluid to move and transfer heat.
Natural Convection Mechanism
The mechanism of natural convection involves the buoyancy of the fluid, which causes it to rise or fall depending on its density. As the fluid moves, it transfers heat from the surface to the surrounding environment. The natural convection mechanism can be enhanced by increasing the temperature difference between the surface and the fluid, or by using a fluid with a higher thermal expansion coefficient. Some key factors that affect natural convection include:
- Temperature difference: The greater the temperature difference, the greater the natural convection.
- Fluid properties: The density, viscosity, and thermal conductivity of the fluid all affect natural convection.
- Surface roughness: A rough surface can enhance natural convection by disrupting the boundary layer.
Types of Natural Convection
There are several types of natural convection, including free convection, forced convection, and mixed convection. Free convection occurs when there is no external force driving the fluid flow, while forced convection occurs when an external force, such as a fan or pump, drives the fluid flow. Mixed convection occurs when both free and forced convection are present. The type of natural convection that occurs depends on the Grashof number, which is a dimensionless parameter that characterizes the relative importance of buoyancy and viscous forces. Some key characteristics of different types of natural convection include:
- Free convection: Occurs when there is no external force driving the fluid flow.
- Forced convection: Occurs when an external force drives the fluid flow.
- Mixed convection: Occurs when both free and forced convection are present.
Natural Convection Applications
Natural convection has many practical applications, including electronic cooling, building insulation, and heat exchanger design. In electronic cooling, natural convection is used to dissipate heat from electronic components, while in building insulation, natural convection is used to reduce heat transfer through walls and roofs. In heat exchanger design, natural convection is used to enhance heat transfer between fluids. Some key considerations for natural convection applications include:
- Heat transfer rate: The rate at which heat is transferred depends on the temperature difference and fluid properties.
- Fluid selection: The fluid used can significantly affect the natural convection process.
- Surface geometry: The shape and size of the surface can affect the natural convection process.
Natural Convection Correlations
There are several correlations that can be used to predict natural convection heat transfer rates, including the Churchill-Chu correlation and the Morgan correlation. These correlations are based on dimensional analysis and experimental data, and can be used to predict natural convection heat transfer rates for a wide range of fluids and surface geometries. Some key factors that affect the accuracy of natural convection correlations include:
- Fluid properties: The density, viscosity, and thermal conductivity of the fluid all affect the natural convection process.
- Surface roughness: A rough surface can enhance natural convection by disrupting the boundary layer.
- Temperature difference: The greater the temperature difference, the greater the natural convection.
Natural Convection Limitations
Natural convection has several limitations, including low heat transfer rates and limited applicability. Natural convection is typically limited to low-temperature applications, and may not be suitable for high-temperature or high-heat-flux applications. Additionally, natural convection can be affected by external factors, such as air currents or vibrations, which can disrupt the natural convection process. Some key considerations for overcoming natural convection limitations include:
- Enhancing fluid properties: Using fluids with high thermal conductivity or low viscosity can enhance natural convection.
- Optimizing surface geometry: Shape and !size of the surface can affect the natural convection process.
- Using active cooling methods: Fans or pumps can be used to enhance natural convection.
What is the formula for the Rayleigh number of a cylinder?

The formula for the Rayleigh number of a cylinder is given by Ra = (g β ΔT L^3) / (ν α), where g is the acceleration due to gravity, β is the volumetric expansion coefficient, ΔT is the temperature difference between the top and bottom surfaces, L is the characteristic length of the cylinder, ν is the kinematic viscosity, and α is the thermal diffusivity.
Introduction to Rayleigh Number
The Rayleigh number is a dimensionless quantity used to predict the onset of convection in a fluid. It is defined as the ratio of the buoyancy force to the viscous force. The formula for the Rayleigh number of a cylinder is used to determine the critical temperature difference at which convection starts. This is important in various engineering applications, such as heat transfer and mass transfer.
- The Rayleigh number is a critical parameter in designing heat exchangers and thermal systems.
- It is used to predict the transition from laminar to turbulent flow in a fluid.
- The Rayleigh number is also used to study natural convection in various geometries, including cylinders and spheres.
Derivation of the Formula
The formula for the Rayleigh number of a cylinder is derived from the Navier-Stokes equations and the energy equation. The Navier-Stokes equations describe the motion of a fluid, while the energy equation describes the heat transfer in the fluid. By combining these equations and using the boundary conditions of the cylinder, the formula for the Rayleigh number can be obtained.
- The Navier-Stokes equations are used to describe the velocity field of the fluid.
- The energy equation is used to describe the temperature field of the fluid.
- The boundary conditions of the cylinder are used to determine the critical temperature difference at which convection starts.
Physical Significance of the Rayleigh Number
The Rayleigh number has a significant impact on the heat transfer and mass transfer in a fluid. When the Rayleigh number is below a certain critical value, the fluid remains stable and conduction is the dominant mode of heat transfer. However, when the Rayleigh number exceeds the critical value, the fluid becomes unstable and convection starts.
- The Rayleigh number is used to predict the onset of convection in a fluid.
- It is used to determine the critical temperature difference at which convection starts.
- The Rayleigh number is also used to study turbulent flow in a fluid.
Applications of the Rayleigh Number
The Rayleigh number has various applications in engineering, including heat exchanger design, thermal system design, and mass transfer. It is also used to study natural convection in various geometries, such as cylinders and spheres.
- The Rayleigh number is used to design heat exchangers and thermal systems.
- It is used to study natural convection in various geometries.
- The Rayleigh number is also used to predict the onset of convection in a fluid.
Limitations of the Rayleigh Number
The Rayleigh number has some limitations, including the assumption of a laminar flow and a constant property fluid. In reality, the flow may be turbulent and the fluid properties may vary with temperature.
- The Rayleigh number assumes a laminar flow, which may not always be the case.
- It assumes a constant property fluid, which may not be accurate.
- The Rayleigh number is only applicable to Newtonian fluids.
What is the convection coefficient of air at 20 °C?
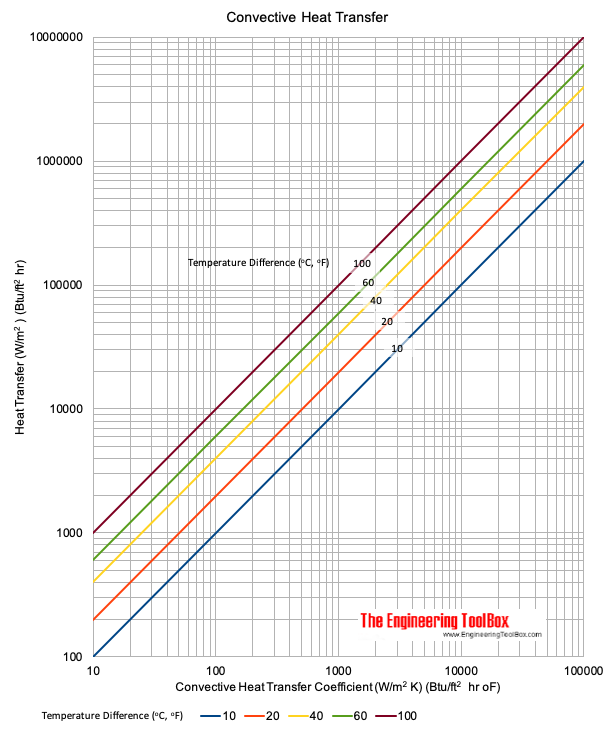
The convection coefficient of air at 20 °C is a measure of the rate of heat transfer between the air and an object due to the movement of air. The convection coefficient is typically denoted by the symbol h and is expressed in units of watts per square meter per degree Celsius (W/m²°C). At 20 °C, the convection coefficient of air is approximately 5-10 W/m²°C for a still air condition. However, this value can increase to 50-100 W/m²°C or more for forced convection conditions, such as in the presence of a fan or wind.
Factors Affecting Convection Coefficient
The convection coefficient is influenced by several factors, including the temperature difference between the air and the object, the velocity of the air, and the surface roughness of the object. Here are some key factors:
- The temperature difference between the air and the object affects the convection coefficient, as a larger temperature difference results in a higher convection coefficient.
- The velocity of the air also affects the convection coefficient, as a higher velocity results in a higher convection coefficient due to the increased turbulence.
- The surface roughness of the object affects the convection coefficient, as a rougher surface results in a higher convection coefficient due to the increased surface area.
Convection Coefficient Calculation
The convection coefficient can be calculated using various empirical correlations, such as the Nusselt number correlation, which takes into account the Reynolds number and the Prandtl number. Here are some steps to calculate the convection coefficient:
- Determine the Nusselt number (Nu) using the empirical correlation.
- Calculate the Reynolds number (Re) based on the air velocity and the object's dimensions.
- Calculate the Prandtl number (Pr) based on the air's thermal properties.
Applications of Convection Coefficient
The convection coefficient has numerous practical applications, including the design of heat exchangers, air conditioning systems, and electronic cooling systems. Here are some examples:
- Heat exchangers: The convection coefficient is used to design heat exchangers, such as air-cooled condensers and liquid-cooled radiators.
- Air conditioning systems: The convection coefficient is used to design air conditioning systems, such as air handlers and fan coils.
- Electronic cooling systems: The convection coefficient is used to design electronic cooling systems, such as heat sinks and fans.
Measurement of Convection Coefficient
The convection coefficient can be measured using various experimental techniques, such as the hot wire anemometry and the infrared thermography. Here are some methods:
- Hot wire anemometry: This method uses a hot wire to measure the air velocity and the convection coefficient.
- Infrared thermography: This method uses an infrared camera to measure the surface temperature and the convection coefficient.
- Heat transfer experiments: This method uses a test rig to measure the heat transfer rate and the convection coefficient.
Limitations of Convection Coefficient
The convection coefficient has some limitations, including the assumptions made in the empirical correlations and the uncertainties in the measurement techniques. Here are some limitations:
- Assumptions: The empirical correlations used to calculate the convection coefficient are based on simplifying assumptions, such as a constant air velocity and a smooth surface.
- Uncertainties: The measurement techniques used to measure the convection coefficient have uncertainties, such as instrumental errors and sampling errors.
- Complex geometries: The convection coefficient can be difficult to calculate for complex geometries, such as fins and tubes.
Frequently Asked Questions (FAQs)
What is the Horizontal Cylinder Natural Convection Equation and how is it used in calculations?
The Horizontal Cylinder Natural Convection Equation is a mathematical formula used to calculate the heat transfer rate from a horizontal cylinder to the surrounding air or fluid. This equation is crucial in various engineering applications, including heat exchangers, pipelines, and tanks, where natural convection plays a significant role in determining the overall heat transfer. The equation takes into account the diameter and length of the cylinder, as well as the temperature difference between the cylinder surface and the surrounding fluid. By using this equation, engineers can predict the heat transfer coefficient and subsequently design more efficient systems. The calculator associated with this equation is a powerful tool that simplifies the calculation process, allowing users to input the relevant parameters and obtain accurate results.
How does the Horizontal Cylinder Natural Convection Equation account for the effects of buoyancy and fluid flow?
The Horizontal Cylinder Natural Convection Equation incorporates the effects of buoyancy and fluid flow through the use of dimensionless parameters, such as the convective heat transfer coefficient and the Grashof number. These parameters characterize the buoyancy-driven flow and turbulence that occur when a horizontal cylinder is immersed in a fluid with a temperature difference. The equation also accounts for the boundary layer that forms around the cylinder, where the fluid velocity and temperature gradients are highest. By considering these factors, the equation provides a more accurate representation of the natural convection process, allowing engineers to design and optimize systems that involve horizontal cylinders. The calculator that accompanies the equation can handle a range of input values, enabling users to explore the effects of different parameters on the heat transfer process.
What are the limitations and assumptions of the Horizontal Cylinder Natural Convection Equation?
The Horizontal Cylinder Natural Convection Equation is based on several assumptions and limitations, which are essential to understand when applying the equation in practice. One key assumption is that the flow is laminar, meaning that the fluid velocity is relatively low and the flow is smooth and continuous. Additionally, the equation assumes that the cylinder is isothermal, meaning that its surface temperature is uniform and constant. The equation also neglects the effects of radiation and conduction, which can be significant in certain applications. Furthermore, the equation is typically valid for a specific range of dimensionless parameters, such as the Rayleigh number and the Prandtl number. When these limitations are exceeded, the equation may not provide accurate results, and alternative methods or equations may be required. The calculator associated with the equation can help users to identify potential limitations and assess the validity of the results.
How can the Horizontal Cylinder Natural Convection Equation be applied in engineering design and optimization?
The Horizontal Cylinder Natural Convection Equation can be applied in a variety of engineering design and optimization contexts, where the goal is to minimize or maximize the heat transfer rate from a horizontal cylinder. For example, in the design of heat exchangers, the equation can be used to determine the optimal diameter and length of the cylinders to achieve a desired heat transfer rate. Similarly, in the optimization of pipelines, the equation can be used to predict the heat transfer rate and determine the required insulation thickness to minimize heat loss. The equation can also be used in feasibility studies to assess the potential for natural convection to occur in a given application. By using the calculator associated with the equation, engineers can quickly and easily explore different design scenarios and optimize their designs to achieve the desired performance. Additionally, the equation can be combined with other equations and models to simulate more complex systems and predict their behavior under various operating conditions.
Deja una respuesta

Entradas Relacionadas