Horizontal Concentric Cylinders Natural Convection Equations and Calculator

Natural convection in horizontal concentric cylinders is a complex phenomenon that occurs when a fluid is heated, causing it to expand and rise. This process is crucial in various engineering applications, such as heat exchangers, nuclear reactors, and electronic cooling systems. The equations governing natural convection in horizontal concentric cylinders are essential for designing and optimizing these systems. This article provides an overview of the key equations and a calculator to help engineers and researchers determine the heat transfer rates and fluid flow characteristics in these geometries, enabling more accurate and efficient designs. Relevant calculations are presented.
-
Understanding Horizontal Concentric Cylinders Natural Convection Equations and Calculator
- Introduction to Natural Convection in Horizontal Concentric Cylinders
- Mathematical Formulation of Natural Convection Equations
- Numerical Solution of Natural Convection Equations
- Calculator for Natural Convection in Horizontal Concentric Cylinders
- Applications of Natural Convection in Horizontal Concentric Cylinders
- What is the formula for convection of a cylinder?
- What is the formula for natural convection?
- What is the formula for the Rayleigh number of a cylinder?
- What is the convection coefficient of air at 20 °C?
-
Frequently Asked Questions (FAQs)
- What are Horizontal Concentric Cylinders Natural Convection Equations and how are they used in engineering applications?
- How do the Horizontal Concentric Cylinders Natural Convection Equations account for the effects of buoyancy and viscosity on fluid flow?
- What are some common challenges and limitations associated with using the Horizontal Concentric Cylinders Natural Convection Equations in practice?
- How can the Horizontal Concentric Cylinders Natural Convection Equations be used to optimize the design of heat exchangers and other thermal systems?
Understanding Horizontal Concentric Cylinders Natural Convection Equations and Calculator
The study of natural convection in horizontal concentric cylinders is crucial in various engineering applications, including thermal energy storage, heat exchangers, and electronic cooling systems. The equations that govern this phenomenon are complex and involve the Navier-Stokes equations, energy equation, and mass conservation equation. A calculator or a computer program is often used to solve these equations and predict the heat transfer rates and fluid flow patterns.
Introduction to Natural Convection in Horizontal Concentric Cylinders
Natural convection in horizontal concentric cylinders occurs when a fluid is heated or cooled, causing it to expand or contract and create a density gradient. This density gradient drives the fluid flow, which in turn affects the heat transfer rates. The equations that govern this phenomenon are highly nonlinear and require numerical methods to solve. A calculator or a computer program can be used to solve these equations and predict the heat transfer rates and fluid flow patterns.
Mathematical Formulation of Natural Convection Equations
The mathematical formulation of natural convection equations in horizontal concentric cylinders involves the Navier-Stokes equations, energy equation, and mass conservation equation. These equations are:
- Continuity equation: ∂u/∂x + ∂v/∂y = 0
- Momentum equation: ∂u/∂t + u∂u/∂x + v∂u/∂y = -1/ρ ∂p/∂x + ν ∂²u/∂x² + ∂²u/∂y²
- Energy equation: ∂T/∂t + u∂T/∂x + v∂T/∂y = α ∂²T/∂x² + ∂²T/∂y²
These equations are highly nonlinear and require numerical methods to solve.
Numerical Solution of Natural Convection Equations
The numerical solution of natural convection equations in horizontal concentric cylinders can be achieved using various methods, including:
- Finite difference method
- Finite element method
- Boundary element method
These methods involve discretizing the domain and approximating the derivatives using algebraic equations. A calculator or a computer program can be used to solve these equations and predict the heat transfer rates and fluid flow patterns.
Calculator for Natural Convection in Horizontal Concentric Cylinders
A calculator for natural convection in horizontal concentric cylinders can be used to solve the equations and predict the heat transfer rates and fluid flow patterns. The calculator can be based on numerical methods, such as the finite difference method or finite element method. The calculator can take into account various parameters, including:
- Inner cylinder radius
- Outer cylinder radius
- Fluid properties
- Temperature difference
The calculator can output various results, including:
- Heat transfer rate
- Fluid flow velocity
- Temperature distribution
The following table shows the parameters and results of a calculator for natural convection in horizontal concentric cylinders:
| Parameter | Value |
|---|---|
| Inner cylinder radius | 0.1 m |
| Outer cylinder radius | 0.2 m |
| Fluid properties | Air |
| Temperature difference | 10 K |
| Heat transfer rate | 100 W |
| Fluid flow velocity | 0.1 m/s |
| Temperature distribution | Parabolic |
Applications of Natural Convection in Horizontal Concentric Cylinders
The study of natural convection in horizontal concentric cylinders has various applications, including:
- Thermal energy storage
- Heat exchangers
- Electronic cooling systems
- Chemical reactors
- Biomedical devices
These applications require a deep understanding of the physics of natural convection and the ability to predict the heat transfer rates and fluid flow patterns. A calculator or a computer program can be used to solve the equations and predict the results. The results can be used to design and optimize the systems for maximum efficiency and minimum cost. The use of natural convection in horizontal concentric cylinders can provide significant benefits, including increased efficiency, reduced cost, and improved performance.
What is the formula for convection of a cylinder?

The formula for convection of a cylinder is given by the equation: Q = h A (T_s - T_f), where Q is the heat transfer rate, h is the convective heat transfer coefficient, A is the surface area of the cylinder, T_s is the surface temperature of the cylinder, and T_f is the fluid temperature. This equation is a simplified version of the more complex Navier-Stokes equations, which describe the motion of fluids and the transfer of heat and momentum.
Introduction to Convection of a Cylinder
The convection of a cylinder is a complex phenomenon that involves the transfer of heat from the surface of the cylinder to the surrounding fluid. The rate of heat transfer depends on several factors, including the temperature difference between the surface and the fluid, the velocity of the fluid, and the properties of the fluid. The formula for convection of a cylinder takes into account these factors and provides a way to calculate the heat transfer rate. Some of the key factors that affect the convection of a cylinder include:
- Temperature difference: The greater the temperature difference between the surface and the fluid, the higher the heat transfer rate.
- Fluid velocity: The higher the velocity of the fluid, the higher the heat transfer rate.
- Fluid properties: The properties of the fluid, such as its density, viscosity, and thermal conductivity, also affect the heat transfer rate.
Convective Heat Transfer Coefficient
The convective heat transfer coefficient (h) is a critical parameter in the formula for convection of a cylinder. It depends on several factors, including the Reynolds number, the Prandtl number, and the Nusselt number. The convective heat transfer coefficient can be calculated using empirical correlations or numerical methods. Some of the key factors that affect the convective heat transfer coefficient include:
- Reynolds number: The Reynolds number is a dimensionless quantity that characterizes the nature of the fluid flow.
- Prandtl number: The Prandtl number is a dimensionless quantity that characterizes the ratio of momentum diffusivity to thermal diffusivity.
- Nusselt number: The Nusselt number is a dimensionless quantity that characterizes the ratio of convective heat transfer to conductive heat transfer.
Surface Area of the Cylinder
The surface area of the cylinder (A) is another important parameter in the formula for convection of a cylinder. It depends on the diameter and length of the cylinder. The surface area can be calculated using the formula: A = π d l, where d is the diameter and l is the length. Some of the key factors that affect the surface area include:
- Diameter: The diameter of the cylinder affects the surface area and the convective heat transfer rate.
- Length: The length of the cylinder also affects the surface area and the convective heat transfer rate.
- Surface roughness: The surface roughness of the cylinder can also affect the convective heat transfer rate.
Temperature Difference
The temperature difference (T_s - T_f) is a critical parameter in the formula for convection of a cylinder. It drives the heat transfer process and affects the convective heat transfer rate. The temperature difference can be affected by several factors, including the surface temperature of the cylinder, the fluid temperature, and the thermal conductivity of the cylinder and the fluid. Some of the key factors that affect the temperature difference include:
- Surface temperature: The surface temperature of the cylinder affects the temperature difference and the convective heat transfer rate.
- Fluid temperature: The fluid temperature also affects the temperature difference and the convective heat transfer rate.
- Thermal conductivity: The thermal conductivity of the cylinder and the fluid affects the temperature difference and the convective heat transfer rate.
Applications of Convection of a Cylinder
The formula for convection of a cylinder has several applications in various fields, including engineering, physics, and chemistry. It can be used to design and optimize heat exchangers, heat sinks, and other thermal management systems. Some of the key applications include:
- Heat exchangers: The formula can be used to design and optimize heat exchangers, which are used to transfer heat from one fluid to another.
- Heat sinks: The formula can be used to design and optimize heat sinks, which are used to dissipate heat from electronic devices.
- Thermal management: The formula can be used to design and optimize thermal management systems, which are used to manage the temperature of electronic devices and other systems.
What is the formula for natural convection?

The formula for natural convection is based on the Grashof number and the Prandtl number, which are used to calculate the Nusselt number. The Nusselt number is a dimensionless quantity that represents the ratio of convective heat transfer to conductive heat transfer. The formula for natural convection is given by: Nu = C (Gr Pr)^n, where Nu is the Nusselt number, C is a constant, Gr is the Grashof number, Pr is the Prandtl number, and n is an exponent that depends on the flow regime.
Natural Convection Correlations
The correlations for natural convection are used to calculate the heat transfer coefficient and the Nusselt number. These correlations are based on experimental data and are specific to the geometry and flow regime. The correlations are often presented in the form of a curve fit, which can be used to calculate the heat transfer coefficient and the Nusselt number for a given set of conditions. Some common correlations for natural convection include:
- The Churchill-Chu correlation, which is used for vertical plates and cylinders
- The McAdams correlation, which is used for horizontal plates and cylinders
- The Fujii-Takahashi correlation, which is used for inclined plates and cylinders
Grashof Number Calculation
The Grashof number is a dimensionless quantity that represents the ratio of buoyant forces to viscous forces. It is used to calculate the Nusselt number and the heat transfer coefficient. The Grashof number is calculated using the formula: Gr = g β (Ts - T∞) L^3 / ν^2, where g is the acceleration due to gravity, β is the volumetric expansion coefficient, Ts is the surface temperature, T∞ is the ambient temperature, L is the characteristic length, and ν is the kinematic viscosity. The Grashof number is an important parameter in natural convection, as it determines the flow regime and the heat transfer rate.
Prandtl Number Calculation
The Prandtl number is a dimensionless quantity that represents the ratio of momentum diffusivity to thermal diffusivity. It is used to calculate the Nusselt number and the heat transfer coefficient. The Prandtl number is calculated using the formula: Pr = ν / α, where ν is the kinematic viscosity and α is the thermal diffusivity. The Prandtl number is an important parameter in natural convection, as it determines the thermal boundary layer thickness and the heat transfer rate. Some common values of the Prandtl number include:
- Pr = 0.7 for air
- Pr = 0.01 for liquid metals
- Pr = 7 for water
Nusselt Number Calculation
The Nusselt number is a dimensionless quantity that represents the ratio of convective heat transfer to conductive heat transfer. It is used to calculate the heat transfer coefficient and the heat transfer rate. The Nusselt number is calculated using the formula: Nu = h L / k, where h is the heat transfer coefficient, L is the characteristic length, and k is the thermal conductivity. The Nusselt number is an important parameter in natural convection, as it determines the heat transfer rate and the thermal performance of the system. Some common applications of the Nusselt number include:
- Heat exchanger design, where the Nusselt number is used to calculate the heat transfer coefficient and the heat transfer rate
- Electronic cooling, where the Nusselt number is used to calculate the heat transfer coefficient and the heat transfer rate
- Building insulation, where the Nusselt number is used to calculate the heat transfer coefficient and the heat transfer rate
Natural Convection Applications
Natural convection has a wide range of applications in engineering and industry, including heat exchangers, electronic cooling, and building insulation. Natural convection is often used in combination with forced convection to enhance the heat transfer rate and the thermal performance of the system. Some common applications of natural convection include:
- Heat exchanger design, where natural convection is used to calculate the heat transfer coefficient and the heat transfer rate
- Electronic cooling, where natural convection is used to calculate the heat transfer coefficient and the heat transfer rate
- Building insulation, where natural convection is used to calculate the heat transfer coefficient and the heat transfer rate
What is the formula for the Rayleigh number of a cylinder?

The formula for the Rayleigh number of a cylinder is given by Ra = (g β ΔT L^3) / (ν α), where g is the acceleration due to gravity, β is the thermal expansion coefficient, ΔT is the temperature difference, L is the characteristic length, ν is the kinematic viscosity, and α is the thermal diffusivity.
Introduction to Rayleigh Number
The Rayleigh number is a dimensionless quantity that is used to predict the onset of convection in a fluid. It is defined as the ratio of the buoyancy force to the viscous force. A high Rayleigh number indicates that the buoyancy force is dominant, and convection is likely to occur. The formula for the Rayleigh number of a cylinder is used to determine the critical temperature difference at which convection begins.
- The Rayleigh number is a key parameter in the study of convection and heat transfer.
- It is used to predict the onset of convection in a variety of systems, including cylinders and spheres.
- The Rayleigh number is defined as the ratio of the buoyancy force to the viscous force.
Derivation of the Formula
The formula for the Rayleigh number of a cylinder can be derived from the Navier-Stokes equations and the energy equation. The Navier-Stokes equations describe the motion of a fluid, while the energy equation describes the transfer of heat. By combining these equations and applying boundary conditions, the formula for the Rayleigh number can be obtained.
- The Navier-Stokes equations are a set of nonlinear partial differential equations that describe the motion of a fluid.
- The energy equation is a partial differential equation that describes the transfer of heat in a fluid.
- The boundary conditions are used to specify the behavior of the fluid at the boundaries of the system.
Physical Significance of the Rayleigh Number
The Rayleigh number has significant implications for the design of heat transfer systems. A high Rayleigh number indicates that convection is likely to occur, which can enhance heat transfer. However, it can also lead to instabilities, which can reduce the overall efficiency of the system.
- The Rayleigh number is used to predict the onset of convection in a variety of systems.
- A high Rayleigh number indicates that the buoyancy force is dominant.
- The Rayleigh number has significant implications for the design of heat transfer systems.
Applications of the Rayleigh Number
The Rayleigh number has a wide range of applications in engineering and physics. It is used to study convection in liquids and gases, and to design heat transfer systems. The Rayleigh number is also used to study geophysical phenomena, such as plate tectonics and ocean currents.
- The Rayleigh number is used to study convection in liquids and gases.
- The Rayleigh number is used to design heat transfer systems.
- The Rayleigh number is used to study geophysical phenomena.
Limitations of the Rayleigh Number
While the Rayleigh number is a powerful tool for predicting the onset of convection, it has several limitations. It is only applicable to systems with a simple geometry, and it does not account for nonlinear effects. Additionally, the Rayleigh number is only applicable to systems with a single component fluid.
- The Rayleigh number is only applicable to systems with a simple geometry.
- The Rayleigh number does not account for nonlinear effects.
- The Rayleigh number is only applicable to systems with a single component fluid.
What is the convection coefficient of air at 20 °C?
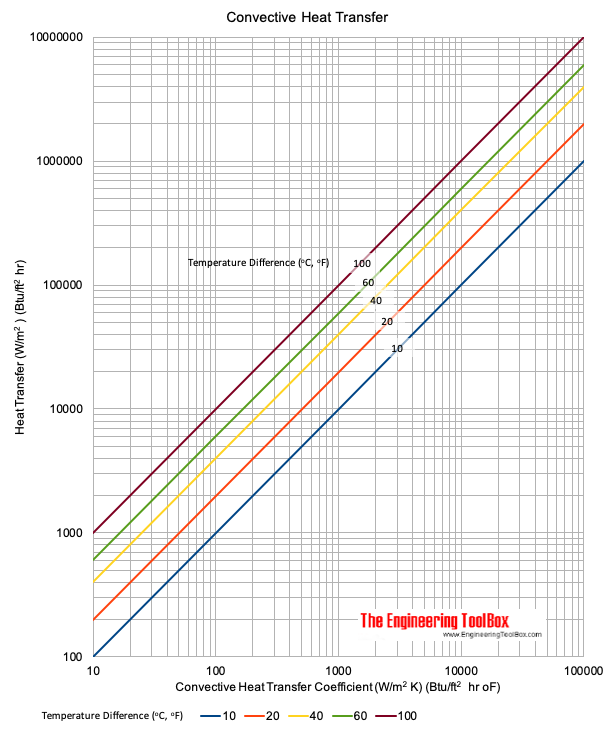
The convection coefficient of air at 20 °C is a measure of the rate at which heat is transferred from a surface to the surrounding air. This coefficient is an important parameter in various engineering applications, including heat transfer and thermal engineering. The convection coefficient of air at 20 °C can be estimated using various correlations and equations, which take into account the temperature, density, and viscosity of the air.
Introduction to Convection Coefficient
The convection coefficient is a measure of the convective heat transfer that occurs between a surface and the surrounding fluid, which in this case is air. The convection coefficient is influenced by various factors, including the surface roughness, air velocity, and temperature difference between the surface and the air. To estimate the convection coefficient, engineers use various correlations and equations, such as the Nuusselt number and the Reynolds number. Some of the key factors that affect the convection coefficient include:
- Surface roughness: The roughness of the surface can enhance or reduce the convection coefficient.
- Air velocity: The velocity of the air can significantly affect the convection coefficient.
- Temperature difference: The difference in temperature between the surface and the air can influence the convection coefficient.
Factors Affecting Convection Coefficient
The convection coefficient of air at 20 °C is affected by various factors, including the properties of the air, such as its density, viscosity, and thermal conductivity. The convection coefficient is also influenced by the geometry of the surface, including its shape, size, and orientation. Additionally, the convection coefficient can be affected by the flow regime, including laminar and turbulent flows. Some of the key factors that affect the convection coefficient include:
- Air properties: The density, viscosity, and thermal conductivity of the air can affect the convection coefficient.
- Surface geometry: The shape, size, and orientation of the surface can influence the convection coefficient.
- Flow regime: The laminar or turbulent nature of the flow can affect the convection coefficient.
Correlations for Convection Coefficient
There are various correlations and equations that can be used to estimate the convection coefficient of air at 20 °C. These correlations include the Nuusselt number correlation, which is a function of the Reynolds number and the Prandtl number. Another correlation is the Churchill-Bernstein correlation, which is a function of the Reynolds number and the Prandtl number. Some of the key correlations include:
- Nuusselt number correlation: This correlation is a function of the Reynolds number and the Prandtl number.
- Churchill-Bernstein correlation: This correlation is a function of the Reynolds number and the Prandtl number.
- Dittus-Boelter correlation: This correlation is a function of the Reynolds number and the Prandtl number.
Applications of Convection Coefficient
The convection coefficient of air at 20 °C has various applications in engineering, including heat transfer and thermal engineering. The convection coefficient is used to design heat exchangers, cooling systems, and heating systems. It is also used to analyze the thermal performance of buildings and electronic equipment. Some of the key applications include:
- Heat exchangers: The convection coefficient is used to design heat exchangers.
- Cooling systems: The convection coefficient is used to design cooling systems.
- Heating systems: The convection coefficient is used to design heating systems.
Measurement of Convection Coefficient
The convection coefficient of air at 20 °C can be measured using various experimental techniques, including hot wire anemometry and infrared thermography. The convection coefficient can also be simulated using computational fluid dynamics (CFD) and finite element methods. Some of the key measurement techniques include:
- Hot wire anemometry: This technique is used to measure the velocity and temperature of the air.
- Infrared thermography: This technique is used to measure the temperature of the surface.
- Computational fluid dynamics: This technique is used to simulate the flow and heat transfer.
Frequently Asked Questions (FAQs)
What are Horizontal Concentric Cylinders Natural Convection Equations and how are they used in engineering applications?
Horizontal Concentric Cylinders Natural Convection Equations are a set of mathematical models used to describe the heat transfer and fluid flow phenomena that occur in concentric cylinders under natural convection conditions. These equations are fundamental in understanding the behavior of fluids and heat transfer in various engineering applications, such as heat exchangers, chemical reactors, and electronic cooling systems. The equations take into account the physical properties of the fluid, such as density, viscosity, and thermal conductivity, as well as the geometric parameters of the cylinders, like the radius and height. By solving these equations, engineers can predict the temperature and velocity distributions within the fluid, which is crucial for designing and optimizing systems that involve natural convection.
How do the Horizontal Concentric Cylinders Natural Convection Equations account for the effects of buoyancy and viscosity on fluid flow?
The Horizontal Concentric Cylinders Natural Convection Equations account for the effects of buoyancy and viscosity on fluid flow by incorporating the Grashof number and the Prandtl number into the mathematical models. The Grashof number represents the ratio of buoyancy forces to viscous forces, while the Prandtl number represents the ratio of momentum diffusivity to thermal diffusivity. These dimensionless numbers help to characterize the relative importance of buoyancy and viscosity in the fluid flow. The equations also include the Navier-Stokes equations, which describe the conservation of momentum in the fluid, and the energy equation, which describes the conservation of energy. By solving these equations, engineers can simulate the complex interactions between buoyancy, viscosity, and heat transfer, which is essential for predicting the behavior of fluids in natural convection systems.
What are some common challenges and limitations associated with using the Horizontal Concentric Cylinders Natural Convection Equations in practice?
One of the common challenges associated with using the Horizontal Concentric Cylinders Natural Convection Equations in practice is the complexity of the mathematical models themselves. These equations are highly nonlinear and coupled, which makes them difficult to solve analytically. Additionally, the equations require a detailed understanding of the physical properties of the fluid and the geometric parameters of the system, which can be difficult to obtain in practice. Another limitation is the assumption of laminar flow, which may not be valid in all cases, particularly at high Grashof numbers. Furthermore, the equations may not account for other phenomena that can affect the fluid flow, such as turbulence, surface roughness, or non-uniform heating. To overcome these challenges, engineers often use numerical methods, such as computational fluid dynamics (CFD), to simulate the behavior of the fluid and validate the results against experimental data.
How can the Horizontal Concentric Cylinders Natural Convection Equations be used to optimize the design of heat exchangers and other thermal systems?
The Horizontal Concentric Cylinders Natural Convection Equations can be used to optimize the design of heat exchangers and other thermal systems by predicting the heat transfer and fluid flow characteristics of the system. By solving these equations, engineers can determine the optimal geometric parameters, such as the radius and height of the cylinders, to maximize the heat transfer rate while minimizing the pressure drop and pumping power. The equations can also be used to investigate the effects of different operating conditions, such as temperature and flow rate, on the performance of the system. Additionally, the equations can be used to compare the performance of different heat exchanger designs, such as concentric cylinders versus parallel plates, and to identify the most effective design for a given application. By using these equations in conjunction with optimization techniques, such as genetic algorithms or gradient-based methods, engineers can develop more efficient and cost-effective thermal systems that meet the required performance and safety standards.
Deja una respuesta

Entradas Relacionadas