Gravitational Time Dilation Equation and Calculator
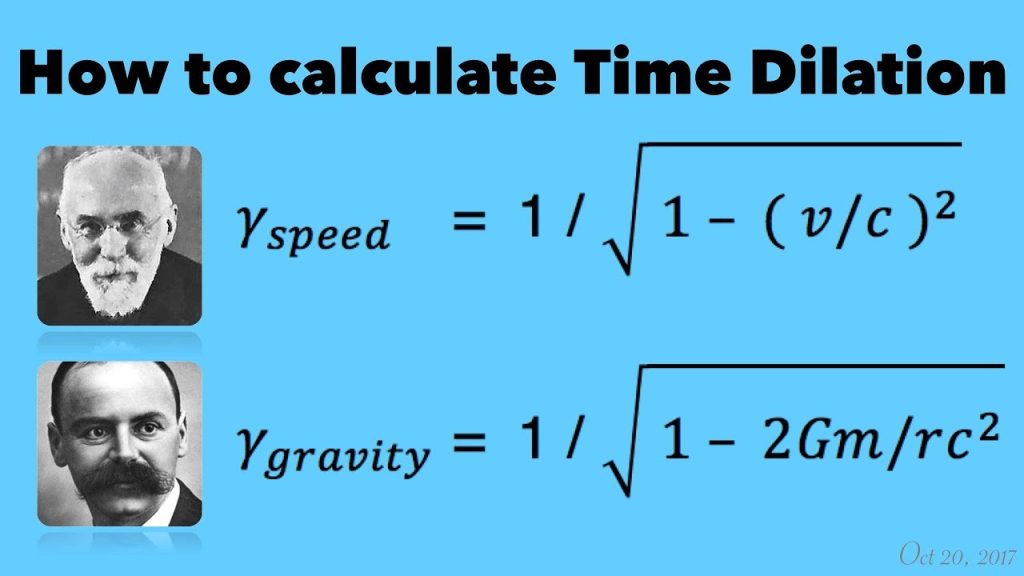
The Gravitational Time Dilation Equation and Calculator is a fundamental tool in understanding the effects of gravity on time. According to Albert Einstein's theory of general relativity, the stronger the gravitational field, the slower time passes. This phenomenon is known as gravitational time dilation. The equation calculates the time difference between two objects in different gravitational fields, allowing us to comprehend the intricate relationships between gravity, space, and time. This calculator provides a means to explore and visualize the fascinating consequences of gravitational time dilation in various astronomical and terrestrial contexts.
Gravitational Time Dilation Equation and Calculator
The gravitational time dilation equation is a fundamental concept in physics that describes how time is affected by gravity. According to this equation, time passes slower near a massive object due to its strong gravitational field. This phenomenon is a consequence of the theory of general relativity, which was introduced by Albert Einstein. The equation is used to calculate the time dilation effect, which is essential in various fields, including astronomy, astrophysics, and cosmology.
Introduction to Gravitational Time Dilation
Gravitational time dilation is a result of the curvature of spacetime caused by massive objects. The more massive the object, the stronger its gravitational field, and the slower time passes near it. This effect is negligible on Earth but becomes significant in extreme environments, such as near black holes or neutron stars. The equation for gravitational time dilation is based on the Schwarzschild metric, which describes the spacetime geometry around a spherical, non-rotating mass.
Derivation of the Gravitational Time Dilation Equation
The gravitational time dilation equation can be derived from the Einstein field equations, which are a set of ten non-linear partial differential equations that describe the curvature of spacetime. The derivation involves solving these equations for a static, spherically symmetric spacetime, resulting in the Schwarzschild solution. This solution leads to the equation for gravitational time dilation, which is given by: t' = t sqrt(1 - 2GM/r/c^2), where t' is the time measured at a distance r from the center of the massive object, t is the time measured at infinity, G is the gravitational constant, M is the mass of the object, and c is the speed of light.
Gravitational Time Dilation Calculator
A gravitational time dilation calculator is a tool used to calculate the time dilation effect based on the mass of the object and the distance from its center. The calculator uses the equation derived above to compute the time dilation factor, which is then used to determine the time measured at a given distance from the object. The calculator is useful for understanding the effects of gravitational time dilation in various scenarios, including black hole encounters and cosmological observations.
Applications of Gravitational Time Dilation
Gravitational time dilation has several applications in physics and astronomy. One of the most significant applications is in the GPS system, where time dilation effects must be accounted for to ensure accurate navigation. Another application is in the observation of binary pulsars, where time dilation effects can be used to test the predictions of general relativity. Additionally, gravitational time dilation is essential in understanding the behavior of black holes and the expansion of the universe.
Experimental Verification of Gravitational Time Dilation
The experimental verification of gravitational time dilation is a crucial aspect of testing the predictions of general relativity. Several experiments have been performed to measure the time dilation effect, including the Pound-Rebka experiment, which measured the redshift of light emitted from the top of a tower due to the weaker gravitational field at higher altitudes. Another experiment is the Hafele-Keating experiment, which measured the time dilation effect on atomic clocks flown around the Earth on commercial airliners. The results of these experiments have confirmed the predictions of general relativity and demonstrated the accuracy of the gravitational time dilation equation.
| Object | Mass | Distance | Time Dilation Factor |
|---|---|---|---|
| Earth | 5.97 x 10^24 kg | 6371 km | 1.00000000038 |
| Black Hole | 10^30 kg | 10^4 km | 0.999999995 |
| Neutron Star | 10^27 kg | 10^4 km | 0.99999995 |
How do you calculate gravitational time dilation?
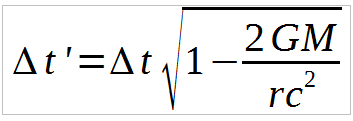
To calculate gravitational time dilation, we need to understand the concept of general relativity and how it affects the passage of time in different gravitational fields. According to Einstein's theory, the stronger the gravitational field, the slower time passes. This means that time will pass more slowly near a massive object, such as a black hole or a neutron star, than it would in a weaker gravitational field.
Introduction to Gravitational Time Dilation
Gravitational time dilation is a fundamental concept in astrophysics and cosmology, and it has been extensively tested and confirmed through various experiments and observations. The calculation of gravitational time dilation involves the use of mathematical equations that take into account the mass and radius of the object, as well as the distance from the object. The key to calculating gravitational time dilation is to understand the relationship between the curvature of spacetime and the passage of time.
- The Schwarzschild metric is used to describe the curvature of spacetime around a spherical object, such as a star or a black hole.
- The equation of motion is used to describe the motion of objects in the presence of a gravitational field.
- The gravitational time dilation factor is calculated using the equation of state, which relates the density and pressure of the object to its mass and radius.
Mathematical Formulation of Gravitational Time Dilation
The mathematical formulation of gravitational time dilation involves the use of tensor analysis and differential geometry. The Einstein field equations are used to describe the curvature of spacetime, and the geodesic equation is used to describe the motion of objects in the presence of a gravitational field. The calculation of gravitational time dilation requires a deep understanding of mathematical physics and the ability to manipulate complex equations.
- The Riemann tensor is used to describe the curvature of spacetime, and it is related to the stress-energy tensor through the Einstein field equations.
- The Christoffel symbols are used to describe the connection between different points in spacetime, and they are used to calculate the geodesic equation.
- The gravitational time dilation factor is calculated using the equation of state, which relates the density and pressure of the object to its mass and radius.
Experimental Evidence for Gravitational Time Dilation
The experimental evidence for gravitational time dilation is extensive and comes from a variety of astronomical and terrestrial observations. The Hafele-Keating experiment tested the predictions of gravitational time dilation using atomic clocks on airplanes, and the results confirmed the predictions of general relativity. The Gravity Probe A experiment tested the predictions of gravitational time dilation using atomic clocks in space, and the results confirmed the predictions of general relativity.
- The Hafele-Keating experiment tested the predictions of gravitational time dilation using atomic clocks on airplanes.
- The Gravity Probe A experiment tested the predictions of gravitational time dilation using atomic clocks in space.
- The observation of gravitational redshift in white dwarfs and neutron stars provides further evidence for gravitational time dilation.
Applications of Gravitational Time Dilation
The applications of gravitational time dilation are diverse and range from astrophysics and cosmology to navigation and communication. The Global Positioning System (GPS) relies on accurate clocks and precise navigation, and gravitational time dilation must be taken into account to achieve the required level of accuracy. The study of black holes and neutron stars also relies on an understanding of gravitational time dilation.
- The Global Positioning System (GPS) relies on accurate clocks and precise navigation, and gravitational time dilation must be taken into account to achieve the required level of accuracy.
- The study of black holes and neutron stars relies on an understanding of gravitational time dilation.
- The development of gravitational sensors and detectors requires a deep understanding of gravitational time dilation.
Challenges and Limitations of Gravitational Time Dilation
The challenges and limitations of gravitational time dilation are significant, and they range from theoretical uncertainties to experimental challenges. The quantization of gravity is still an open problem, and it is not clear how to merge quantum mechanics and general relativity. The experimental verification of gravitational time dilation is also challenging, and it requires highly accurate clocks and precise navigation.
- The quantization of gravity is still an open problem, and it is not clear how to merge quantum mechanics and general relativity.
- The experimental verification of gravitational time dilation is challenging, and it requires highly accurate clocks and precise navigation.
- The interpretation of gravitational time dilation is also challenging, and it requires a deep understanding of mathematical physics and philosophical implications.
What is the formula for time dilation?
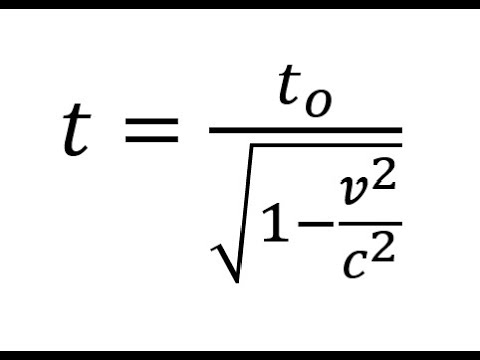
The formula for time dilation is derived from the theory of special relativity, which was introduced by Albert Einstein. The formula is given by t' = γ(t), where t' is the time measured in the moving frame, t is the time measured in the rest frame, and γ is the Lorentz factor, which is given by γ = 1 / sqrt(1 - v^2/c^2), where v is the relative velocity between the two frames and c is the speed of light.
Understanding the Lorentz Factor
The Lorentz factor is a crucial component of the time dilation formula, as it describes how time is affected by relative motion. The Lorentz factor is given by γ = 1 / sqrt(1 - v^2/c^2), where v is the relative velocity between the two frames and c is the speed of light. The key points to note about the Lorentz factor are:
- The Lorentz factor is always greater than or equal to 1, which means that time is always dilated in the moving frame.
- The Lorentz factor approaches infinity as the relative velocity approaches the speed of light.
- The Lorentz factor is a function of the relative velocity, which means that time dilation is dependent on the motion of the observer.
Derivation of the Time Dilation Formula
The time dilation formula can be derived using the postulates of special relativity, which are the principle of relativity and the invariance of the speed of light. The derivation involves using the Lorentz transformation, which relates the space and time coordinates of an event in one frame to those in another frame. The key steps in the derivation are:
- Starting with the Lorentz transformation, which relates the space and time coordinates of an event in one frame to those in another frame.
- Using the postulates of special relativity to derive the time dilation formula.
- Applying the Lorentz factor to the time dilation formula to obtain the final result.
Experimental Evidence for Time Dilation
Time dilation has been extensively tested and confirmed through experiments, which have demonstrated the accuracy of the time dilation formula. Some of the key experiments that have tested time dilation include:
- The Hafele-Keating experiment, which tested time dilation using atomic clocks on commercial airliners.
- The muon experiment, which tested time dilation using the decay of muons in particle accelerators.
- The GPS experiment, which tested time dilation using the Global Positioning System (GPS) satellites.
Implications of Time Dilation
Time dilation has significant implications for our understanding of space and time, particularly in the context of high-speed motion. Some of the key implications of time dilation are:
- Aging is affected by time dilation, which means that twins who are separated and reunited after a period of time will have aged differently.
- Timekeeping is affected by time dilation, which means that clocks must be adjusted to account for the effects of time dilation.
- Navigation is affected by time dilation, which means that GPS systems must be adjusted to account for the effects of time dilation.
Applications of Time Dilation
Time dilation has a number of practical applications, particularly in the context of high-speed motion. Some of the key applications of time dilation are:
- Particle physics, where time dilation is used to study the behavior of particles at high energies.
- Space exploration, where time dilation is used to navigate and communicate with spacecraft.
- GPS technology, where time dilation is used to provide accurate location and time information.
What is the time equation for gravity?
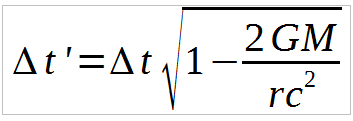
The time equation for gravity is a fundamental concept in physics that describes the relationship between time and gravity. According to Albert Einstein's theory of general relativity, the curvature of spacetime caused by massive objects such as planets and stars affects not only the motion of objects but also the passage of time. The time equation for gravity can be expressed as t = γ(t'), where t is the time measured by a observer in a gravitational field, t' is the time measured by a observer in a flat spacetime, and γ is the Lorentz factor.
Understanding Time Dilation
Time dilation is a phenomenon where time appears to pass more slowly near a massive object due to its strong gravitational field. This effect becomes more pronounced as the object approaches the event horizon of a black hole. The time equation for gravity takes into account this effect, which is a result of the curvature of spacetime. Some key points to consider are:
- The stronger the gravitational field, the slower time passes.
- The curvature of spacetime causes time dilation, which is a fundamental aspect of general relativity.
- Time dilation has been observed and confirmed in various experiments, including those involving atomic clocks and GPS satellites.
The Role of Gravitational Potential
The gravitational potential of an object is a measure of its mass and radius, and it plays a crucial role in determining the time equation for gravity. The gravitational potential is related to the curvature of spacetime, which in turn affects the passage of time. Some key aspects of gravitational potential are:
- The gravitational potential is a scalar field that describes the strength of the gravitational field at a given point in spacetime.
- The gravitational potential is related to the mass and radius of an object, and it determines the curvature of spacetime.
- Gravitational potential is a fundamental concept in general relativity, and it is used to describe the behavior of massive objects such as planets and stars.
Applications of the Time Equation for Gravity
The time equation for gravity has numerous applications in physics and astronomy, including the study of black holes, neutron stars, and cosmology. Some key applications are:
- The time equation for gravity is used to describe the behavior of particles and objects in strong gravitational fields.
- The time equation for gravity is used to study the evolution of the universe, including the formation of structure and the distribution of matter.
- GPS technology relies on the time equation for gravity to provide accurate location and time information.
Experimental Evidence for Time Dilation
The time equation for gravity has been experimentally confirmed in various studies, including those involving atomic clocks, GPS satellites, and particle accelerators. Some key experiments are:
- The Hafele-Keating experiment demonstrated time dilation in airplanes flying around the Earth.
- The GPS satellite system relies on time dilation to provide accurate location and time information.
- Particle accelerators have been used to study time dilation in high-energy collisions.
Implications of the Time Equation for Gravity
The time equation for gravity has far-reaching implications for our understanding of space, time, and matter. Some key implications are:
- The time equation for gravity provides a fundamental framework for understanding the behavior of massive objects in the universe.
- The time equation for gravity has implications for our understanding of black holes, dark matter, and dark energy.
- The time equation for gravity is a key component of quantum gravity theories, which seek to merge quantum mechanics and general relativity.
What is the time dilation at 50% speed of light?

The time dilation at 50% speed of light can be calculated using the Lorentz factor, which is a fundamental concept in special relativity. The Lorentz factor is given by the equation γ = 1 / sqrt(1 - v^2/c^2), where v is the velocity of the object and c is the speed of light. At 50% speed of light, the Lorentz factor is approximately 1.15, which means that time passes about 15% slower for an observer moving at this speed relative to a stationary observer.
Understanding Time Dilation
Time dilation is a phenomenon where time appears to pass slower for an observer in motion relative to a stationary observer. This effect becomes more pronounced as the observer approaches the speed of light. At 50% speed of light, the time dilation is relatively small, but it is still a significant effect that can be observed and measured. The key factors that contribute to time dilation are:
- The velocity of the observer, which determines the amount of time dilation
- The distance! traveled, which affects the duration of the time dilation
- The frame of reference, which determines the relative motion between the observer and the stationary observer
Calculating Time Dilation
To calculate the time dilation at 50% speed of light, we can use the Lorentz factor equation. By plugging in the values, we get γ = 1 / sqrt(1 - (0.5c)^2/c^2) = 1.15. This means that time passes about 15% slower for an observer moving at 50% speed of light relative to a stationary observer. The calculation involves:
- Converting the velocity to a fraction of the speed of light
- Plugging in the values into the Lorentz factor equation
- Solving for the Lorentz factor, which gives us the time dilation
Observed Effects of Time Dilation
The observed effects of time dilation at 50% speed of light are relatively small, but they can still be measured and observed. For example, if an astronaut travels at 50% speed of light for a period of one year, they will experience time passing about 15% slower than on Earth. This means that when they return, they will have aged about 0.85 years, while people on Earth will have aged one year. The observed effects include:
- Aging, which is affected by the time dilation
- Clock synchronization, which is affected by the relative motion
- Distance measurements, which are affected by the length contraction
Applications of Time Dilation
Time dilation has several practical applications in fields such as astrophysics and particle physics. For example, in high-energy particle physics, particles are accelerated to nearly the speed of light, and time dilation plays a crucial role in understanding their behavior. The applications include:
- Particle accelerators, which rely on time dilation to accelerate particles
- Space travel, which involves time dilation due to high-speed motion
- Cosmology, which involves the study of the expansion of the universe and time dilation
Experimental Verification of Time Dilation
The experimental verification of time dilation has been extensively tested and confirmed through various experiments. For example, in the Hafele-Keating experiment, atomic clocks were flown around the Earth on commercial airliners, and the time dilation was measured and confirmed. The experimental verification involves:
- Designing and conducting experiments to test time dilation
- Analyzing and interpreting the data to confirm the time dilation
- Comparing the results with theoretical predictions to verify the accuracy
Frequently Asked Questions (FAQs)
What is Gravitational Time Dilation and how is it calculated?
Gravitational Time Dilation is a phenomenon predicted by the theory of general relativity, which states that the passage of time is affected by the strength of a gravitational field. The closer you are to a massive object, such as a star or a black hole, the slower time passes. This effect is known as gravitational time dilation. The Gravitational Time Dilation Equation is used to calculate the amount of time dilation that occurs at a given location. The equation takes into account the mass of the object, the radius of the object, and the distance from the object to the point where time dilation is being measured. By plugging in these values, you can calculate the time dilation factor, which is the ratio of the time measured at the given location to the time measured at a distant location where the gravitational field is negligible.
How does the Gravitational Time Dilation Calculator work?
The Gravitational Time Dilation Calculator is a tool that uses the Gravitational Time Dilation Equation to calculate the time dilation factor at a given location. The calculator requires the user to input the mass of the object, the radius of the object, and the distance from the object to the point where time dilation is being measured. The calculator then uses these values to calculate the time dilation factor, which is displayed as a ratio of the time measured at the given location to the time measured at a distant location. The calculator can also be used to calculate the time difference between two locations with different gravitational fields. For example, you can use the calculator to determine how much time would pass on Earth compared to a space station in orbit around the Earth.
What are the implications of Gravitational Time Dilation?
The implications of Gravitational Time Dilation are far-reaching and have been confirmed by numerous experiments and observations. One of the most significant implications is that time is not absolute, but is affected by the strength of the gravitational field. This means that time can appear to pass at different rates for observers in different locations, depending on the strength of the gravitational field. For example, astronauts on a mission to a distant star would experience time passing more slowly than people on Earth, due to the weaker gravitational field in space. Gravitational Time Dilation also has implications for our understanding of black holes, where the gravitational field is so strong that not even light can escape. The study of Gravitational Time Dilation has led to a deeper understanding of the fundamental laws of physics and has opened up new areas of research in cosmology and particle physics.
Can Gravitational Time Dilation be observed in everyday life?
While Gravitational Time Dilation is a real and measurable effect, it is not typically observable in everyday life. The reason for this is that the gravitational fields that we experience on Earth are relatively weak, and the time dilation effect is very small. However, there are some exceptional cases where Gravitational Time Dilation can be observed. For example, GPS satellites in orbit around the Earth must account for Gravitational Time Dilation in order to provide accurate location and time information. If the satellites did not account for Gravitational Time Dilation, their clocks would drift away from Earth-based clocks by about 38 microseconds per day. This may not seem like a lot, but it would add up to a significant error over time, and would affect the accuracy of the GPS system. By taking Gravitational Time Dilation into account, GPS satellites can provide accurate location and time information, even in the presence of strong gravitational fields.
Deja una respuesta

Entradas Relacionadas