Extension Spring Rate Constant Calculator and Formula
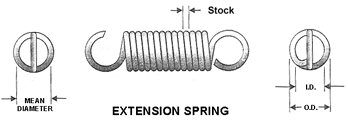
The extension spring rate constant is a critical parameter in designing and selecting the appropriate spring for various applications. It determines the amount of force required to extend or compress the spring by a certain distance. Calculating this constant is essential to ensure the spring's performance and longevity. The extension spring rate constant calculator and formula provide a straightforward method to determine this value, taking into account the spring's physical properties and dimensions, such as wire diameter, coil diameter, and number of coils. This calculator simplifies the calculation process, saving time and effort.
-
Understanding the Extension Spring Rate Constant Calculator and Formula
- What is the Extension Spring Rate Constant Calculator?
- How to Use the Extension Spring Rate Constant Formula
- Applications of the Extension Spring Rate Constant Calculator and Formula
- Limitations of the Extension Spring Rate Constant Calculator and Formula
- Comparison of Different Extension Spring Rate Constant Calculators and Formulas
- How to calculate extension spring constant?
- How do you calculate the spring constant K?
- What is the formula for the spring constant of the extension mass?
- What is the formula for K in spring rate?
-
Frequently Asked Questions (FAQs)
- What is the Extension Spring Rate Constant Calculator and how does it work?
- What is the formula used to calculate the Extension Spring Rate Constant?
- How do I use the Extension Spring Rate Constant Calculator to determine the spring rate constant?
- What are the limitations and assumptions of the Extension Spring Rate Constant Calculator?
Understanding the Extension Spring Rate Constant Calculator and Formula
The Extension Spring Rate Constant Calculator and Formula are essential tools in the field of physics and engineering, particularly when dealing with springs and their behavior under different conditions. The spring rate constant, also known as the spring constant, is a measure of the stiffness of a spring. It is defined as the ratio of the force applied to the spring to the resulting displacement. The formula to calculate the spring rate constant is given by k = F / x, where k is the spring rate constant, F is the force applied, and x is the resulting displacement.
What is the Extension Spring Rate Constant Calculator?
The Extension Spring Rate Constant Calculator is an online tool that allows users to calculate the spring rate constant of an extension spring. It is a simple and easy-to-use calculator that requires the user to input the force and displacement values, and then calculates the spring rate constant using the formula k = F / x. The calculator is useful for engineers and physicists who need to determine the stiffness of a spring in various applications.
How to Use the Extension Spring Rate Constant Formula
To use the Extension Spring Rate Constant Formula, users need to have the force and displacement values. The formula is k = F / x, where k is the spring rate constant, F is the force applied, and x is the resulting displacement. For example, if a force of 10 N is applied to a spring and the resulting displacement is 0.5 m, the spring rate constant can be calculated as k = 10 N / 0.5 m = 20 N/m.
Applications of the Extension Spring Rate Constant Calculator and Formula
The Extension Spring Rate Constant Calculator and Formula have various applications in physics and engineering. They are used to design and analyze springs and spring-based systems, such as suspension systems in vehicles, door closers, and exercise equipment. The calculator and formula are also used to determine the stiffness of a spring, which is essential in understanding its behavior under different conditions.
Limitations of the Extension Spring Rate Constant Calculator and Formula
The Extension Spring Rate Constant Calculator and Formula have some limitations. They assume that the spring is ideal and that the force and displacement values are accurate. In reality, springs can be non-ideal and have non-linear behavior, which can affect the accuracy of the calculations. Additionally, the calculator and formula do not take into account other factors that can affect the behavior of a spring, such as friction and damping.
Comparison of Different Extension Spring Rate Constant Calculators and Formulas
There are different Extension Spring Rate Constant Calculators and Formulas available, each with its own strengths and weaknesses. Some calculators and formulas use simplified models, while others use complex models that take into account non-linear behavior and other factors. The choice of calculator or formula depends on the specific application and the desired level of accuracy. The following table compares some of the different calculators and formulas:
| Calculator/Formula | Strengths | Weaknesses |
|---|---|---|
| Simple Calculator | Easy to use, fast calculations | Limited accuracy, assumes ideal spring |
| Complex Calculator | High accuracy, takes into account non-linear behavior | Difficult to use, slow calculations |
| Hooke's Law Formula | Well-established, widely used | Assumes ideal spring, limited accuracy |
The Extension Spring Rate Constant Calculator and Formula are powerful tools for understanding the behavior of springs and spring-based systems. By using these tools, engineers and physicists can design and analyze springs and spring-based systems with increased accuracy and confidence.
How to calculate extension spring constant?

To calculate the extension spring constant, you need to understand the relationship between the spring's physical properties and its behavior under load. The spring constant is a measure of the spring's stiffness, and it is typically denoted by the symbol k. The extension spring constant can be calculated using the following formula: k = F / δ, where F is the force applied to the spring and δ is the resulting displacement.
Understanding Spring Properties
To calculate the extension spring constant, you need to understand the spring's physical properties, such as its wire diameter, coil diameter, and number of coils. These properties affect the spring's stiffness and its ability to stretch or compress under load. The following are some key factors to consider when calculating the extension spring constant:
- The spring's wire diameter affects its stiffness, with thicker wires resulting in a stiffer spring.
- The coil diameter also affects the spring's stiffness, with larger coils resulting in a less stiff spring.
- The number of coils affects the spring's ability to stretch or compress, with more coils resulting in a longer spring.
Calculating Spring Constant Using Formula
The extension spring constant can be calculated using the formula k = F / δ, where F is the force applied to the spring and δ is the resulting displacement. This formula can be rearranged to solve for F or δ, depending on the known values. For example, if you know the spring constant and the displacement, you can calculate the force required to achieve that displacement. The following are some steps to follow when calculating the spring constant:
- Measure the force applied to the spring using a force sensor or load cell.
- Measure the resulting displacement using a displacement sensor or linear encoder.
- Plug the values into the formula k = F / δ to calculate the spring constant.
Selecting the Right Spring Material
The spring material affects the spring's stiffness and its ability to stretch or compress under load. Common spring materials include steel, stainless steel, and titanium, each with its own unique properties and characteristics. The following are some factors to consider when selecting a spring material:
- The material's yield strength affects the spring's ability to stretch or compress without deforming.
- The material's elastic modulus affects the spring's stiffness and its ability to return to its original shape after load is removed.
- The material's corrosion resistance affects the spring's ability to withstand corrosive environments.
Understanding Spring Terminology
To calculate the extension spring constant, you need to understand spring terminology, such as free length, solid height, and spring rate. The free length is the spring's length when it is not under load, while the solid height is the spring's length when it is fully compressed. The spring rate is the spring's stiffness, typically measured in pounds per inch or newtons per millimeter. The following are some key terms to understand:
- The spring's free length affects its ability to stretch or compress under load.
- The spring's solid height affects its ability to compress under load.
- The spring's spring rate affects its stiffness and its ability to return to its original shape after load is removed.
Considering Safety Factors
When calculating the extension spring constant, you need to consider safety factors, such as the spring's ability to withstand overload and its potential for failure. The spring's safety factor is typically calculated as the ratio of its ultimate strength to its yield strength. A higher safety factor indicates a lower risk of failure. The following are some factors to consider when evaluating safety factors:
- The spring's ultimate strength affects its ability to withstand overload.
- The spring's yield strength affects its ability to stretch or compress without deforming.
- The spring's safety factor affects its potential for failure and its ability to withstand corrosive environments.
How do you calculate the spring constant K?

To calculate the spring constant K, you need to understand the relationship between the force applied to a spring and its resulting displacement. The spring constant is a measure of the stiffness of a spring, and it can be calculated using Hooke's Law, which states that the force required to stretch or compress a spring is proportional to its displacement from its equilibrium position.
Understanding Hooke's Law
Hooke's Law is a fundamental principle in physics that describes the relationship between the force applied to a spring and its resulting displacement. According to Hooke's Law, the force F required to stretch or compress a spring is proportional to its displacement x from its equilibrium position. The spring constant K is the constant of proportionality in this relationship. The formula for Hooke's Law is F = Kx, where F is the force, K is the spring constant, and x is the displacement.
- The force F is typically measured in Newtons (N)
- The displacement x is typically measured in meters (m)
- The spring constant K is typically measured in Newtons per meter (N/m)
Calculating Spring Constant using Hooke's Law
To calculate the spring constant K, you can use the formula F = Kx, where F is the force, K is the spring constant, and x is the displacement. By rearranging this formula, you can solve for K: K = F/x. This means that if you know the force required to stretch or compress a spring and the resulting displacement, you can calculate the spring constant.
- Measure the force F required to stretch or compress the spring
- Measure the resulting displacement x from the equilibrium position
- Use the formula K = F/x to calculate the spring constant
Experimental Methods for Measuring Spring Constant
There are several experimental methods for measuring the spring constant of a spring, including the use of a spring scale or a force sensor. One common method involves attaching a mass to the end of the spring and measuring the resulting displacement. The force exerted on the spring can be calculated using the weight of the mass, and the spring constant can be calculated using Hooke's Law.
- Attach a mass to the end of the spring
- Measure the resulting displacement from the equilibrium position
- Calculate the force exerted on the spring using the weight of the mass
Factors Affecting Spring Constant
The spring constant of a spring can be affected by several factors, including the material it is made of, its length, and its cross-sectional area. For example, a spring made of a stiffer material will have a higher spring constant than a spring made of a softer material. Similarly, a longer spring will have a lower spring constant than a shorter spring.
- The material the spring is made of can affect its spring constant
- The length of the spring can affect its spring constant
- The cross-sectional area of the spring can affect its spring constant
Real-World Applications of Spring Constant
The spring constant has many real-world applications, including the design of suspension systems in cars, the development of exercise equipment, and the creation of medical devices. In each of these applications, the spring constant is used to predict the behavior of a spring under different loads and conditions.
- The spring constant is used in the design of suspension systems in cars
- The spring constant is used in the development of exercise equipment
- The spring constant is used in the creation of medical devices
What is the formula for the spring constant of the extension mass?

The formula for the spring constant of an extension mass is given by the equation k = (F / x), where k is the spring constant, F is the force applied to the spring, and x is the displacement of the spring from its equilibrium position. This formula is derived from Hooke's Law, which states that the force required to stretch or compress a spring is proportional to the displacement of the spring.
Understanding the Spring Constant
The spring constant is a measure of the stiffness of a spring, and it is an important parameter in the design and analysis of mechanical systems. The spring constant is typically denoted by the symbol k and is measured in units of Newtons per meter (N/m). To calculate the spring constant, we can use the following formula:
- The force applied to the spring is measured in Newtons (N).
- The displacement of the spring is measured in meters (m).
- The spring constant is calculated by dividing the force by the displacement.
Factors Affecting the Spring Constant
The spring constant of an extension mass is affected by several factors, including the material of the spring, the dimension of the spring, and the temperature of the spring. For example, a spring made of a stiffer material will have a higher spring constant than a spring made of a softer material. Additionally, a spring with a larger diameter will have a higher spring constant than a spring with a smaller diameter.
- The material of the spring affects its stiffness and strength.
- The dimension of the spring affects its stiffness and flexibility.
- The temperature of the spring affects its stiffness and performance.
Applications of the Spring Constant
The spring constant has many practical applications in engineering and physics, including the design of mechanical systems, the analysis of vibrations, and the measurement of forces. For example, the spring constant is used to calculate the frequency of vibrations in a system, and it is also used to design springs for specific applications.
- The spring constant is used to design mechanical systems.
- The spring constant is used to analyze vibrations.
- The spring constant is used to measure forces.
Measurement of the Spring Constant
The spring constant can be measured using a variety of methods, including the use of a force sensor and a displacement sensor. The force sensor measures the force applied to the spring, while the displacement sensor measures the displacement of the spring. By dividing the force by the displacement, we can calculate the spring constant.
- The force sensor measures the force applied to the spring.
- The displacement sensor measures the displacement of the spring.
- The spring constant is calculated by dividing the force by the displacement.
Importance of the Spring Constant
The spring constant is a critical parameter in the analysis and design of mechanical systems, and it is essential to understand its significance and application. The spring constant affects the behavior of a system, including its stability, vibrations, and performance. By understanding the spring constant, we can design and analyze mechanical systems more effectively.
- The spring constant affects the stability of a system.
- The spring constant affects the vibrations of a system.
- The spring constant affects the performance of a system.
What is the formula for K in spring rate?

The formula for K in spring rate is given by Hooke's Law, which states that the force (F) exerted by a spring is proportional to its displacement (x) from its equilibrium position. The spring constant (K) is a measure of the spring's stiffness, and it is defined as the ratio of the force applied to the spring to the resulting displacement. The formula for K is: K = F / x. This formula can be used to calculate the spring rate of a spring, which is a measure of how much force is required to compress or extend the spring by a certain amount.
Understanding Spring Rate
The spring rate is an important parameter in the design and analysis of springs, as it determines how much force is required to compress or extend the spring. The formula for K can be used to calculate the spring rate, which is typically expressed in units of force per unit displacement, such as newtons per meter (N/m) or pounds per inch (lb/in). To calculate the spring rate, the following steps can be taken:
- Determine the force applied to the spring, which can be measured using a force sensor or calculated using the spring's geometry and material properties.
- Measure the displacement of the spring, which can be done using a displacement sensor or by measuring the change in length of the spring.
- Use the formula K = F / x to calculate the spring constant, which can then be used to calculate the spring rate.
Factors Affecting Spring Rate
The spring rate of a spring can be affected by several factors, including the material properties of the spring, such as its elastic modulus and Poisson's ratio. The geometry of the spring, including its length, diameter, and coil pitch, can also affect the spring rate. Additionally, the operating conditions of the spring, such as the temperature and environmental conditions, can also impact the spring rate. The following factors can affect the spring rate:
- The material properties of the spring, which can affect its stiffness and damping characteristics.
- The geometry of the spring, which can affect its spring rate and displacement characteristics.
- The operating conditions of the spring, which can affect its performance and lifespan.
Calculating Spring Rate
To calculate the spring rate, the formula K = F / x can be used, where F is the force applied to the spring and x is the displacement of the spring. The spring constant (K) can be calculated by measuring the force and displacement of the spring, and then using the formula to calculate the spring rate. The following steps can be taken to calculate the spring rate:
- Measure the force applied to the spring, which can be done using a force sensor or by calculating the force using the spring's geometry and material properties.
- Measure the displacement of the spring, which can be done using a displacement sensor or by measuring the change in length of the spring.
- Use the formula K = F / x to calculate the spring constant, which can then be used to calculate the spring rate.
Applications of Spring Rate
The spring rate is an important parameter in the design and analysis of springs, and it has a wide range of applications in various fields, including mechanical engineering, aerospace engineering, and automotive engineering. The spring rate is used to design and optimize suspension systems, vibration isolators, and shock absorbers, among other applications. The following are some examples of applications of spring rate:
- Suspension systems, where the spring rate is used to design and optimize the suspension system to provide a smooth ride and stable handling.
- Vibration isolators, where the spring rate is used to design and optimize the vibration isolator to reduce the transmission of vibrations to sensitive components.
- Shock absorbers, where the spring rate is used to design and optimize the shock absorber to provide a smooth ride and stable handling.
Importance of Spring Rate
The spring rate is a critical parameter in the design and analysis of springs, and it plays a crucial role in determining the performance and lifespan of the spring. A high spring rate can result in a stiff spring that is prone to fatigue and failure, while a low spring rate can result in a soft spring that is prone to deformation and instability. The following are some reasons why the spring rate is important:
- The spring rate affects the stiffness and damping characteristics of the spring, which can impact the performance and lifespan of the spring.
- The spring rate affects the displacement and force characteristics of the spring, which can impact the design and optimization of the spring.
- The spring rate affects the safety and reliability of the spring, which can impact the overall performance and lifespan of the system.
Frequently Asked Questions (FAQs)
What is the Extension Spring Rate Constant Calculator and how does it work?
The Extension Spring Rate Constant Calculator is a tool used to calculate the spring rate constant of an extension spring, which is a critical parameter in determining the spring's behavior under various loading conditions. The calculator uses the formula for the spring rate constant, which is based on the spring's physical properties, such as its wire diameter, coil diameter, and number of coils. By inputting these values into the calculator, users can quickly and accurately determine the spring rate constant, which is essential for designing and selecting the appropriate extension spring for a specific application. The calculator is particularly useful for engineers and designers who need to specify the correct spring for their projects, as well as for manufacturers who need to ensure that their springs meet the required specifications.
What is the formula used to calculate the Extension Spring Rate Constant?
The formula used to calculate the Extension Spring Rate Constant is based on the spring's physical properties and is given by the equation: k = (G d^4) / (8 n D^3), where k is the spring rate constant, G is the shear modulus of the spring material, d is the wire diameter, n is the number of coils, and D is the coil diameter. This formula takes into account the geometric properties of the spring, as well as the material properties, to provide an accurate calculation of the spring rate constant. The spring rate constant is a critical parameter in determining the spring's behavior, as it affects the force required to compress or extend the spring, and is therefore essential for designing and selecting the appropriate extension spring for a specific application.
How do I use the Extension Spring Rate Constant Calculator to determine the spring rate constant?
To use the Extension Spring Rate Constant Calculator, users need to input the physical properties of the spring, including the wire diameter, coil diameter, and number of coils. The calculator will then use the formula to calculate the spring rate constant and display the result. Users can also input the desired spring rate constant and the calculator will determine the required physical properties of the spring. This feature is particularly useful for designers and engineers who need to specify the correct spring for their projects. Additionally, the calculator can be used to compare different spring designs and determine the optimal spring configuration for a specific application.
What are the limitations and assumptions of the Extension Spring Rate Constant Calculator?
The Extension Spring Rate Constant Calculator is based on a number of assumptions and limitations that users should be aware of. For example, the calculator assumes that the spring is made of a linear elastic material and that the load is applied axially. Additionally, the calculator does not take into account friction or hysteresis effects, which can affect the spring's behavior. Users should also be aware that the spring rate constant can vary depending on the temperature and environmental conditions in which the spring is used. Therefore, users should consult the manufacturer's specifications and test data to ensure that the calculated spring rate constant is accurate and reliable for their specific application.
Deja una respuesta

Entradas Relacionadas