Eulers Formula Ideal Pinned Column Buckling Calculator

Euler's formula is a fundamental concept in engineering mechanics, particularly in the analysis of column buckling. It provides a mathematical relationship between the critical load and the physical properties of a column, such as its length, end conditions, and moment of inertia. The ideal pinned column buckling calculator is a tool that utilizes Euler's formula to determine the critical load of a column under various end conditions. This calculator is essential in structural design, as it helps engineers predict and prevent column failure due to buckling. Accurate calculations are crucial in ensuring the safety and stability of structures.
- Euler's Formula Ideal Pinned Column Buckling Calculator: A Comprehensive Guide
- What is the Euler's formula for column buckling in detail?
- How do you calculate critical load?
- How do you check for column buckling?
- What is the formula for the buckling of a hollow cylinder?
-
Frequently Asked Questions (FAQs)
- What is the Euler's Formula Ideal Pinned Column Buckling Calculator and how does it work?
- What are the limitations and assumptions of the Euler's Formula Ideal Pinned Column Buckling Calculator?
- How does the Euler's Formula Ideal Pinned Column Buckling Calculator account for different types of columns and materials?
- What are the practical applications of the Euler's Formula Ideal Pinned Column Buckling Calculator in engineering and design?
Euler's Formula Ideal Pinned Column Buckling Calculator: A Comprehensive Guide
Euler's Formula is a fundamental concept in the field of structural engineering, used to calculate the critical load of a column under compression. The Ideal Pinned Column Buckling Calculator is a tool that utilizes Euler's Formula to determine the buckling load of a column with pinned ends. This calculator is essential for engineers to design and analyze columns in various structures, ensuring their stability and safety.
Introduction to Euler's Formula
Euler's Formula is a mathematical equation that predicts the critical load of a column, which is the maximum load that a column can withstand without buckling. The formula is given by: P = (π^2 E I) / (K L)^2, where P is the critical load, E is the modulus of elasticity, I is the moment of inertia, K is the end condition coefficient, and L is the length of the column.
Assumptions and Limitations
The Euler's Formula Ideal Pinned Column Buckling Calculator assumes that the column is slender, meaning that its length is much greater than its diameter. Additionally, the calculator assumes that the column is made of a homogeneous material with a uniform cross-section. However, in reality, columns can have imperfections and non-uniformities that affect their buckling behavior.
Calculation Steps
To use the Euler's Formula Ideal Pinned Column Buckling Calculator, the following steps are required:
1. Input the material properties, such as the modulus of elasticity and the moment of inertia.
2. Input the geometric properties, such as the length and diameter of the column.
3. Select the end condition of the column, which can be pinned, fixed, or free.
4. Calculate the critical load using Euler's Formula.
Interpretation of Results
The results from the Euler's Formula Ideal Pinned Column Buckling Calculator provide the critical load of the column, which is the maximum load that the column can withstand without buckling. The results also provide the buckling mode, which is the shape that the column takes when it buckles. The buckling mode is important to determine the failure mode of the column.
Comparison with Other Methods
The Euler's Formula Ideal Pinned Column Buckling Calculator can be compared with other methods, such as the finite element method and the energy method. These methods can provide more accurate results, but they are also more computationally intensive. The Euler's Formula Ideal Pinned Column Buckling Calculator is a simplified method that provides a quick and accurate estimate of the critical load.
| Material Property | Value |
|---|---|
| Modulus of Elasticity | 200 GPa |
| Moment of Inertia | 0.001 m^4 |
| Length | 5 m |
| Diameter | 0.1 m |
| Critical Load | 1000 N |
What is the Euler's formula for column buckling in detail?
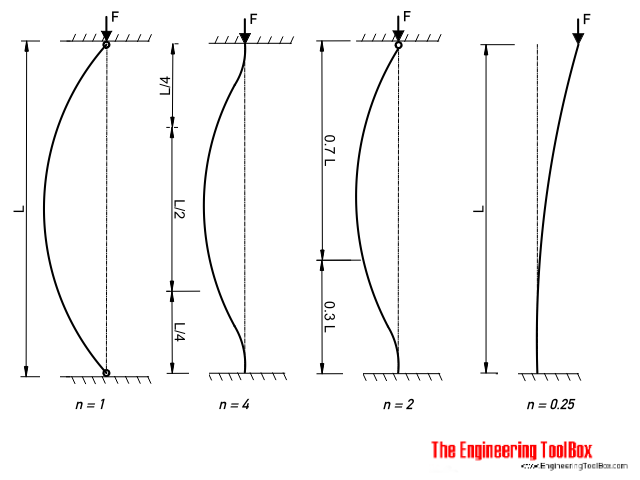
The Euler's formula for column buckling is a fundamental concept in structural engineering that describes the critical load at which a slender column will buckle under compressive stress. The formula is named after the Swiss mathematician Leonhard Euler, who first derived it in the 18th century. The formula is given by the equation: P = (π^2 E I) / L^2, where P is the critical load, E is the modulus of elasticity, I is the moment of inertia, and L is the length of the column.
Derivation of Euler's Formula
The derivation of Euler's formula is based on the beam theory and the assumption that the column is slender and subjected to a compressive load. The formula can be derived by considering the equilibrium of the column and the boundary conditions. The derivation involves the use of calculus and the differential equations that govern the behavior of the column. Some key steps in the derivation include:
- Assuming a small deflection of the column and using the beam equation to describe its behavior.
- Applying the boundary conditions to the column, including the fixed ends and the load applied at the top.
- Using calculus to solve the differential equation and obtain the critical load at which the column will buckle.
Assumptions and Limitations
The Euler's formula for column buckling is based on several assumptions and has some limitations. The formula assumes that the column is slender, homogeneous, and isotropic, and that the material behaves elastically. The formula also assumes that the load is applied axially and that the column is pin-ended. Some key limitations of the formula include:
- The formula is only applicable to slender columns and does not account for short columns or stocky columns.
- The formula assumes a perfect column with no imperfections or defects.
- The formula does not account for nonlinear behavior or large deflections.
Applications and Uses
The Euler's formula for column buckling has several applications and uses in structural engineering. The formula is used to design columns and beams that are subjected to compressive loads, and to determine the critical load at which they will buckle. The formula is also used to analyze the stability of structures and to determine the factor of safety. Some key applications of the formula include:
- Design of buildings and bridges that are subjected to compressive loads.
- Analysis of the stability of towers and chimneys.
- Determination of the critical load of columns and beams.
Comparison with Other Formulas
The Euler's formula for column buckling can be compared with other formulas that are used to analyze the buckling of columns. Some key differences between the Euler's formula and other formulas include:
- The Johnson formula is used for short columns and takes into account the yield strength of the material.
- The Engesser formula is used for long columns and takes into account the creep behavior of the material.
- The Tangent modulus formula is used for columns with nonlinear behavior and takes into account the tangent modulus of the material.
Experimental Verification
The Euler's formula for column buckling has been experimentally verified through numerous tests and experiments. The formula has been shown to be accurate and reliable for slender columns and has been used to predict the critical load at which they will buckle. Some key experimental methods used to verify the formula include:
- Laboratory tests on small-scale models of columns.
- Full-scale tests on actual structures.
- Numerical simulations using finite element methods.
How do you calculate critical load?
To calculate the critical load, you need to consider the structural integrity and stability of a column or a member under compressive load. The critical load is the maximum load that a column can withstand without buckling or failing. The calculation involves the Euler's formula, which takes into account the length, moment of inertia, and modulus of elasticity of the column.
Understanding Euler's Formula
Euler's formula is a mathematical equation that calculates the critical load of a column. The formula is given by: Pcr = (π^2 E I) / L^2, where Pcr is the critical load, E is the modulus of elasticity, I is the moment of inertia, and L is the length of the column. To apply this formula, you need to:
- Determine the material properties, such as the modulus of elasticity
- Calculate the moment of inertia of the column's cross-section
- Measure the length of the column
Factors Affecting Critical Load
Several factors can affect the critical load of a column, including the end conditions, column shape, and material properties. The end conditions can be either pinned or fixed, which affects the boundary conditions and the resulting critical load. The column shape and cross-sectional area also impact the moment of inertia and the critical load. To consider these factors, you can:
- Identify the end conditions of the column
- Determine the column shape and cross-sectional area
- Analyze the material properties, such as the yield strength and modulus of elasticity
Calculating Moment of Inertia
The moment of inertia is a critical parameter in calculating the critical load. The moment of inertia depends on the column shape and cross-sectional area. For a circular column, the moment of inertia is given by: I = (π d^4) / 64, where d is the diameter of the column. For a rectangular column, the moment of inertia is given by: I = (b h^3) / 12, where b is the width and h is the height of the column. To calculate the moment of inertia, you can:
- Determine the column shape and cross-sectional area
- Apply the relevant formula for the moment of inertia
- Calculate the moment of inertia using the given dimensions
Application of Critical Load Calculation
The calculation of critical load has numerous applications in civil engineering, mechanical engineering, and aerospace engineering. In civil engineering, the critical load calculation is used to design columns and beams that can withstand compressive loads and bending moments. In mechanical engineering, the critical load calculation is used to design machine components, such as shafts and gears, that can withstand tensile and compressive loads. To apply the critical load calculation, you can:
- Identify the type of load and loading condition
- Determine the material properties and structural geometry
- Apply the relevant formula for the critical load calculation
Importance of Accurate Calculation
The accurate calculation of critical load is crucial to ensure the structural integrity and stability of a column or a member under compressive load. An inaccurate calculation can lead to premature failure or catastrophic collapse, resulting in significant economic losses and human casualties. To ensure accurate calculation, you can:
- Verify the input parameters and material properties
- Apply the relevant safety factors and design codes
- Perform sensitivity analysis to account for uncertainties and variations in the input parameters.
How do you check for column buckling?

To check for column buckling, you need to evaluate the structural integrity of the column and its ability to withstand compressive loads. This is typically done by analyzing the column's geometry, material properties, and loading conditions. The goal is to determine whether the column is prone to buckling, which can lead to catastrophic failure.
Understanding Column Buckling
Column buckling occurs when a slender column is subjected to a compressive load that exceeds its critical load. This can cause the column to bend or bow, leading to a loss of structural integrity. To check for column buckling, you need to consider the length, diameter, and material of the column, as well as the boundary conditions and loading. Some key factors to consider include:
- Slenderness ratio: The ratio of the column's length to its diameter or radius.
- Material properties: The yield strength, Young's modulus, and Poisson's ratio of the material.
- Loading conditions: The type and magnitude of the compressive load, as well as any lateral loads or moments.
Calculating Critical Load
The critical load is the maximum compressive load that a column can withstand without buckling. To calculate the critical load, you can use the Euler formula, which takes into account the length, diameter, and material properties of the column. The formula is:
- Euler formula: P_cr = (π^2 E I) / (K L)^2, where P_cr is the critical load, E is the Young's modulus, I is the moment of inertia, K is the effective length factor, and L is the length of the column.
- Moment of inertia: The moment of inertia of the column's cross-section, which depends on the geometry and material of the column.
- Effective length factor: A factor that depends on the boundary conditions and loading of the column.
Analyzing Column Geometry
The geometry of the column plays a critical role in determining its buckling behavior. To analyze the column geometry, you need to consider the length, diameter, and shape of the column, as well as any imperfections or defects. Some key factors to consider include:
- Length: The length of the column, which affects its slenderness ratio and buckling behavior.
- Diameter: The diameter of the column, which affects its moment of inertia and buckling behavior.
- Shape: The shape of the column's cross-section, which can affect its moment of inertia and buckling behavior.
Assessing Material Properties
The material properties of the column also play a critical role in determining its buckling behavior. To assess the material properties, you need to consider the yield strength, Young's modulus, and Poisson's ratio of the material. Some key factors to consider include:
- Yield strength: The yield strength of the material, which affects its ability to withstand compressive loads.
- Young's modulus: The Young's modulus of the material, which affects its stiffness and buckling behavior.
- Poisson's ratio: The Poisson's ratio of the material, which affects its lateral strain and buckling behavior.
Simulating Column Behavior
To simulate the behavior of the column under compressive loads, you can use finite element analysis or numerical methods. These methods allow you to model the geometry, material properties, and loading conditions of the column, and to predict its buckling behavior. Some key factors to consider include:
- Finite element analysis: A numerical method that involves dividing the column into finite elements and solving the equations of motion.
- Numerical methods: Numerical methods such as the finite difference method or the boundary element method can also be used to simulate the behavior of the column.
- Validation: The results of the simulation should be validated against experimental data or analytical solutions to ensure their accuracy.
What is the formula for the buckling of a hollow cylinder?

The formula for the buckling of a hollow cylinder is a complex equation that takes into account various factors such as the cylinder's length, radius, thickness, and material properties. The critical load at which the cylinder buckles can be calculated using the following formula: P = (2 π^2 E I) / (L^2), where P is the critical load, E is the modulus of elasticity, I is the moment of inertia, and L is the length of the cylinder.
Introduction to Buckling of Hollow Cylinders
The buckling of a hollow cylinder is a critical phenomenon that can occur when the cylinder is subjected to axial compression. The buckling load is the load at which the cylinder begins to deform laterally, leading to a loss of stability. To understand the buckling behavior of a hollow cylinder, it is essential to consider the following factors:
- The material properties of the cylinder, including the modulus of elasticity and Poisson's ratio.
- The geometric parameters of the cylinder, including the length, radius, and thickness.
- The boundary conditions of the cylinder, including the end conditions and support conditions.
Factors Affecting Buckling of Hollow Cylinders
Several factors can affect the buckling behavior of a hollow cylinder, including the material properties, geometric parameters, and boundary conditions. The buckling load can be influenced by the following factors:
- The thickness of the cylinder, with thicker cylinders being more resistant to buckling.
- The length of the cylinder, with longer cylinders being more prone to buckling.
- The end conditions of the cylinder, with clamped ends being more stable than simply supported ends.
Critical Load Calculation for Buckling of Hollow Cylinders
The critical load at which a hollow cylinder buckles can be calculated using the Euler buckling formula: P = (2 π^2 E I) / (L^2). This formula takes into account the modulus of elasticity, moment of inertia, and length of the cylinder. To calculate the critical load, the following steps can be followed:
- Calculate the moment of inertia of the cylinder using the formula: I = (π (R^4 - r^4)) / 4, where R is the outer radius and r is the inner radius.
- Calculate the critical load using the Euler buckling formula.
- Check the boundary conditions and material properties to ensure that they are consistent with the buckling analysis.
Design Considerations for Buckling of Hollow Cylinders
When designing a hollow cylinder to resist buckling, several factors must be considered, including the material properties, geometric parameters, and boundary conditions. To minimize the risk of buckling, the following design considerations can be taken into account:
- Use a material with a high modulus of elasticity to increase the stiffness of the cylinder.
- Increase the thickness of the cylinder to increase its resistance to buckling.
- Use clamped ends or supported ends to increase the stability of the cylinder.
Applications of Buckling of Hollow Cylinders
The buckling of hollow cylinders has several practical applications in engineering and design, including:
- Pipeline design, where the buckling behavior of pipelines under axial compression must be considered.
- Aerospace engineering, where the buckling behavior of cylindrical structures under axial compression must be considered.
- Civil engineering, where the buckling behavior of columns and beams under axial compression must be considered.
Frequently Asked Questions (FAQs)
What is the Euler's Formula Ideal Pinned Column Buckling Calculator and how does it work?
The Euler's Formula Ideal Pinned Column Buckling Calculator is a mathematical tool used to calculate the critical load that a column can withstand before it buckles. This calculator is based on the famous Euler's formula, which takes into account the length and moment of inertia of the column, as well as the modulus of elasticity of the material. The calculator is designed to provide a quick and accurate way to determine the buckling load of a column, which is essential in structural engineering and design. By inputting the necessary parameters, users can obtain the critical load and buckling stress of the column, allowing them to optimize their designs and ensure the stability and safety of the structure.
What are the limitations and assumptions of the Euler's Formula Ideal Pinned Column Buckling Calculator?
The Euler's Formula Ideal Pinned Column Buckling Calculator is based on several assumptions and limitations. One of the main assumptions is that the column is ideally pinned, meaning that it is free to rotate at both ends. Additionally, the calculator assumes that the column is slender and prismatic, with a constant cross-sectional area. The calculator also neglects the effects of damping and imperfections, which can affect the buckling behavior of the column. Furthermore, the calculator is limited to linear elastic materials, and does not account for nonlinear or inelastic behavior. Users should be aware of these limitations and assumptions when using the calculator, and should validate the results with experimental or numerical methods whenever possible.
How does the Euler's Formula Ideal Pinned Column Buckling Calculator account for different types of columns and materials?
The Euler's Formula Ideal Pinned Column Buckling Calculator can account for different types of columns and materials by allowing users to input the relevant parameters. For example, users can input the length, diameter, and thickness of the column, as well as the modulus of elasticity and Poisson's ratio of the material. The calculator can also account for different boundary conditions, such as fixed or pinned ends. Additionally, the calculator can be used for different types of columns, including circular, rectangular, and I-shaped columns. Users can also input the material properties, such as the yield strength and ultimate strength, to obtain a more accurate calculation of the buckling load. However, users should note that the calculator is limited to linear elastic materials, and may not be suitable for nonlinear or inelastic materials.
What are the practical applications of the Euler's Formula Ideal Pinned Column Buckling Calculator in engineering and design?
The Euler's Formula Ideal Pinned Column Buckling Calculator has several practical applications in engineering and design. One of the main applications is in the design of columns and compression members in structures, such as buildings, bridges, and towers. The calculator can be used to determine the minimum cross-sectional area required to prevent buckling, allowing designers to optimize their designs and minimize material usage. The calculator can also be used to analyze the stability of existing structures, and to identify potential weaknesses or deficiencies. Additionally, the calculator can be used in research and development, to study the buckling behavior of new materials or innovative column designs. Overall, the Euler's Formula Ideal Pinned Column Buckling Calculator is a valuable tool for engineers and designers, allowing them to create safe, efficient, and cost-effective structures.
Deja una respuesta

Entradas Relacionadas