Cube Flow Perpendicular to Face Surface Drag, Drag Coefficient Equation and Calculator

The drag force exerted on a cube flowing perpendicular to its face surface is a complex phenomenon that depends on various factors, including the cube's velocity, density, and surface area. Understanding the drag coefficient equation is crucial in calculating the drag force, which is essential in designing and optimizing systems involving fluid flow and cube interaction. This article provides an in-depth examination of the drag coefficient equation and offers a calculator to simplify the calculation process, enabling engineers and researchers to accurately predict and analyze the drag force in various applications. The equation is a key component.
- Cube Flow Perpendicular to Face Surface Drag, Drag Coefficient Equation and Calculator
- What is the drag coefficient of a plate perpendicular to the flow?
- How does CFD calculate drag coefficient?
- What is the drag coefficient of a cube?
- What is the formula for drag flow?
-
Frequently Asked Questions (FAQs)
- What is Cube Flow Perpendicular to Face Surface Drag and how does it affect the Drag Coefficient Equation?
- How does the Drag Coefficient Equation change when calculating Cube Flow Perpendicular to Face Surface Drag?
- What are the key factors that affect the Drag Coefficient Equation when calculating Cube Flow Perpendicular to Face Surface Drag?
- How can the Cube Flow Perpendicular to Face Surface Drag Calculator be used to simplify the calculation of the Drag Coefficient Equation?
Cube Flow Perpendicular to Face Surface Drag, Drag Coefficient Equation and Calculator
The drag coefficient is a dimensionless quantity that is used to quantify the amount of drag force experienced by an object as it moves through a fluid, such as air or water. In the case of a cube, the drag coefficient is an important parameter in determining the drag force that acts on the cube as it moves through a fluid. The drag coefficient equation is a mathematical formula that is used to calculate the drag force experienced by an object, and it takes into account the density of the fluid, the velocity of the object, and the surface area of the object.
Introduction to Cube Flow Perpendicular to Face Surface Drag
The cube flow perpendicular to face surface drag is a type of fluid dynamics problem that involves the flow of a fluid around a cube-shaped object. In this type of problem, the fluid flows perpendicular to one of the faces of the cube, and the drag force that acts on the cube is dependent on the velocity of the fluid, the density of the fluid, and the surface area of the cube. The drag coefficient equation can be used to calculate the drag force experienced by the cube, and it is an important parameter in determining the motion of the cube through the fluid.
Drag Coefficient Equation and Calculator
The drag coefficient equation is a mathematical formula that is used to calculate the drag force experienced by an object as it moves through a fluid. The equation is given by: F_d = ½ ρ v^2 C_d A, where F_d is the drag force, ρ is the density of the fluid, v is the velocity of the object, C_d is the drag coefficient, and A is the surface area of the object. A calculator can be used to solve this equation and determine the drag force experienced by the cube.
Factors that Affect the Drag Coefficient
There are several factors that can affect the drag coefficient of a cube, including the shape of the cube, the size of the cube, and the surface roughness of the cube. The shape of the cube can affect the drag coefficient by changing the way that the fluid flows around the cube. The size of the cube can also affect the drag coefficient by changing the surface area of the cube. The surface roughness of the cube can also affect the drag coefficient by changing the way that the fluid interacts with the surface of the cube.
Applications of the Drag Coefficient Equation
The drag coefficient equation has several applications in engineering and physics, including the design of aircraft, vehicles, and buildings. The equation can be used to calculate the drag force that acts on an object as it moves through a fluid, and it is an important parameter in determining the motion of the object. The equation can also be used to optimize the shape and size of an object to reduce the drag force that acts on it.
Limitations of the Drag Coefficient Equation
The drag coefficient equation has several limitations, including the assumption that the fluid is incompressible and that the flow is steady. The equation also assumes that the surface roughness of the object is negligible, and that the shape of the object is simple. In reality, the flow around an object can be complex and turbulent, and the drag coefficient can vary depending on the conditions of the flow.
| Parameter | Unit | Description |
|---|---|---|
| Drag Coefficient | Unitless | A dimensionless quantity that quantifies the amount of drag force experienced by an object |
| Density | kg/m^3 | The mass per unit volume of the fluid |
| Velocity | m/s | The speed at which the object moves through the fluid |
| Surface Area | m^2 | The area of the object that is in contact with the fluid |
What is the drag coefficient of a plate perpendicular to the flow?
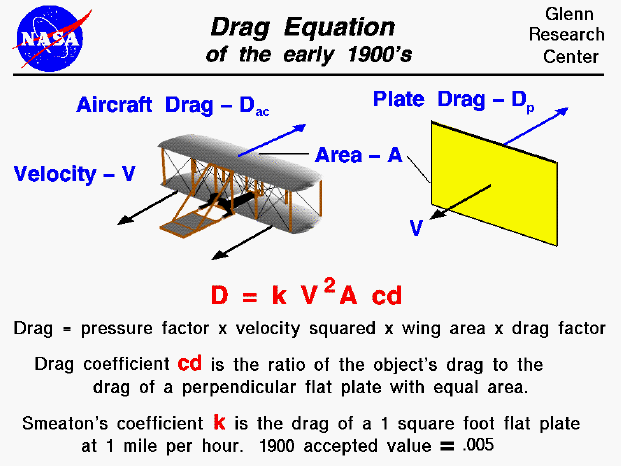
The drag coefficient of a plate perpendicular to the flow is a value that represents the ratio of the drag force acting on the plate to the dynamic pressure of the fluid flow. This value is important in the field of fluid dynamics and aerodynamics, as it can be used to calculate the drag force acting on an object and to optimize its shape for minimal drag.
Introduction to Drag Coefficient
The drag coefficient is a dimensionless value that depends on the shape of the object and the Reynolds number of the flow. For a plate perpendicular to the flow, the drag coefficient is typically around 1.28, but this value can vary depending on the surface roughness and edge effects. The drag coefficient can be calculated using the following formula: Cd = Fd / (0.5 ρ v^2 A), where Fd is the drag force, ρ is the fluid density, v is the fluid velocity, and A is the cross-sectional area of the plate.
- The drag force is the force that opposes the motion of the object through the fluid.
- The dynamic pressure is the pressure exerted by the fluid on the object due to its motion.
- The Reynolds number is a dimensionless value that characterizes the nature of the fluid flow.
Factors Affecting Drag Coefficient
There are several factors that can affect the drag coefficient of a plate perpendicular to the flow, including the surface roughness, edge effects, and turbulence. The surface roughness can increase the drag coefficient by creating a turbulent boundary layer that increases the drag force. The edge effects can also increase the drag coefficient by creating a vortex that increases the drag force.
- The surface roughness can increase the drag coefficient by up to 50%.
- The edge effects can increase the drag coefficient by up to 20%.
- The turbulence can increase the drag coefficient by up to 10%.
Calculating Drag Coefficient
The drag coefficient can be calculated using the formula: Cd = Fd / (0.5 ρ v^2 A), where Fd is the drag force, ρ is the fluid density, v is the fluid velocity, and A is the cross-sectional area of the plate. This formula can be used to calculate the drag coefficient for a plate perpendicular to the flow, as well as for other shapes and orientations.
- The drag force can be measured using a force balance or a load cell.
- The fluid density can be measured using a hydrometer or a density meter.
- The fluid velocity can be measured using a pitot tube or a hot wire anemometer.
Applications of Drag Coefficient
The drag coefficient has many practical applications in the field of fluid dynamics and aerodynamics, including the design of aircraft, automobiles, and wind turbines. By optimizing the shape of an object to minimize its drag coefficient, engineers can reduce the drag force and increase the efficiency of the object.
- The aircraft industry uses the drag coefficient to optimize the shape of airfoils and fuselages.
- The automobile industry uses the drag coefficient to optimize the shape of bodies and wheels.
- The wind turbine industry uses the drag coefficient to optimize the shape of blades and hubs.
Experimental Methods for Measuring Drag Coefficient
There are several experimental methods that can be used to measure the drag coefficient of a plate perpendicular to the flow, including wind tunnel testing and water channel testing. These methods involve measuring the drag force and dynamic pressure of the flow, and then using the formula: Cd = Fd / (0.5 ρ v^2 A) to calculate the drag coefficient.
- The wind tunnel testing method involves measuring the drag force and dynamic pressure of the flow in a wind tunnel.
- The water channel testing method involves measuring the drag force and dynamic pressure of the flow in a water channel.
- The computational fluid dynamics method involves using computer simulations to calculate the drag coefficient.
How does CFD calculate drag coefficient?
The calculation of the drag coefficient in Computational Fluid Dynamics (CFD) involves solving the Navier-Stokes equations, which describe the motion of fluid substances such as liquids and gases. The drag coefficient is a dimensionless quantity that is used to quantify the amount of drag force exerted on an object as it moves through a fluid. The calculation of the drag coefficient in CFD typically involves the following steps:
First, the geometry of the object is defined, and a mesh is generated to discretize the computational domain. Then, the Navier-Stokes equations are solved using a numerical method, such as the finite element method or the finite volume method. The solution of the Navier-Stokes equations provides the velocity and pressure fields around the object, which are then used to calculate the drag force. Finally, the drag coefficient is calculated by dividing the drag force by the dynamic pressure and the reference area of the object.
Introduction
The drag coefficient is an important parameter in fluid dynamics, as it is used to predict the drag force exerted on an object as it moves through a fluid. The calculation of the drag coefficient in CFD involves solving the Navier-Stokes equations, which describe the motion of fluid substances. Some of the key factors that affect the drag coefficient include:
- Geometry of the object: The shape and size of the object can significantly affect the drag coefficient.
- Velocity of the object: The speed at which the object moves through the fluid can also affect the drag coefficient.
- Density of the fluid: The density of the fluid can affect the drag coefficient, as it affects the dynamic pressure and the reference area of the object.
Governing Equations
The calculation of the drag coefficient in CFD involves solving the Navier-Stokes equations, which are a set of nonlinear partial differential equations that describe the motion of fluid substances. The Navier-Stokes equations consist of the continuity equation, the momentum equation, and the energy equation. The solution of the Navier-Stokes equations provides the velocity and pressure fields around the object, which are then used to calculate the drag force. Some of the key assumptions made in the calculation of the drag coefficient include:
- Incompressible flow: The fluid is assumed to be incompressible, meaning that its density remains constant.
- Laminar flow: The flow is assumed to be laminar, meaning that it is smooth and continuous.
- Steady-state flow: The flow is assumed to be steady-state, meaning that it does not change over time.
Numerical Methods
The calculation of the drag coefficient in CFD typically involves the use of numerical methods, such as the finite element method or the finite volume method. These methods involve discretizing the computational domain into a mesh, and then solving the Navier-Stokes equations using a numerical algorithm. Some of the key advantages of numerical methods include:
- High accuracy: Numerical methods can provide high accuracy solutions to the Navier-Stokes equations.
- Flexibility: Numerical methods can be used to model complex geometries and flow conditions.
- Efficiency: Numerical methods can be computationally efficient, making them suitable for large-scale simulations.
Validation and Verification
The calculation of the drag coefficient in CFD requires validation and verification to ensure that the results are accurate and reliable. Validation involves comparing the results of the simulation with experimental data, while verification involves checking the numerical implementation of the Navier-Stokes equations. Some of the key methods used for validation and verification include:
- Experimental data: Experimental data is used to validate the results of the simulation.
- Analytical solutions: Analytical solutions are used to verify the numerical implementation of the Navier-Stokes equations.
- Grid convergence studies: Grid convergence studies are used to verify the accuracy of the numerical solution.
Applications
The calculation of the drag coefficient in CFD has a wide range of applications in various fields, including aerospace engineering, automotive engineering, and civil engineering. Some of the key applications include:
- Aircraft design: The drag coefficient is used to predict the drag force exerted on an aircraft as it moves through the air.
- Car design: The drag coefficient is used to predict the drag force exerted on a car as it moves through the air.
- Bridge design: The drag coefficient is used to predict the drag force exerted on a bridge as it is exposed to strong winds.
What is the drag coefficient of a cube?
The drag coefficient of a cube is a measure of the resistance it experiences as it moves through a fluid, such as air or water. The drag coefficient is a dimensionless quantity that depends on the shape and size of the cube, as well as the velocity and density of the fluid. For a cube, the drag coefficient is typically around 1.05 to 1.15, although this value can vary depending on the specific conditions.
Understanding the Drag Coefficient
The drag coefficient is an important parameter in aerodynamics and hydrodynamics, as it determines the force exerted on an object as it moves through a fluid. To calculate the drag coefficient of a cube, we need to consider the following factors:
- Reynolds number: The Reynolds number is a dimensionless quantity that characterizes the nature of fluid flow around the cube.
- Surface roughness: The surface roughness of the cube can affect the drag coefficient, with rougher surfaces typically experiencing more turbulence.
- Angle of attack: The angle of attack is the angle between the cube's surface and the oncoming fluid flow, which can impact the drag coefficient.
Factors Affecting the Drag Coefficient
The drag coefficient of a cube is influenced by various factors, including the velocity of the fluid, the density of the fluid, and the size and shape of the cube. Other factors, such as turbulence and surface roughness, can also play a significant role. To minimize the drag coefficient, it is essential to optimize the design of the cube and consider the following:
- Streamlining: Streamlining the cube's shape can reduce the drag coefficient by minimizing the cross-sectional area.
- Surface smoothness: Ensuring a smooth surface can reduce turbulence and minimize the drag coefficient.
- Size reduction: Reducing the size of the cube can decrease the drag coefficient by reducing the frontal area.
Applications of the Drag Coefficient
The drag coefficient of a cube has numerous practical applications in various fields, including aerospace engineering, automotive engineering, and civil engineering. For instance, understanding the drag coefficient can help design more efficient aircraft, cars, and buildings. Additionally, the drag coefficient is essential in:
- Wind tunnel testing: Wind tunnel testing relies on the drag coefficient to measure the aerodynamic performance of objects.
- Computational fluid dynamics: Computational fluid dynamics uses the drag coefficient to simulate fluid flow around complex shapes.
- Structural analysis: Structural analysis considers the drag coefficient to assess the stability of structures under wind loads.
Calculating the Drag Coefficient
To calculate the drag coefficient of a cube, we can use empirical formulas or computational methods. The most common method involves using the drag equation, which relates the drag force to the velocity, density, and frontal area of the cube. The drag equation is:
- Drag force: The drag force is proportional to the velocity squared and the density of the fluid.
- Frontal area: The frontal area is the cross-sectional area of the cube perpendicular to the fluid flow.
- Drag coefficient: The drag coefficient is a dimensionless quantity that depends on the shape and size of the cube.
Experimental Methods for Measuring the Drag Coefficient
Experimental methods can be used to measure the drag coefficient of a cube, including wind tunnel testing and water tank testing. These methods involve measuring the drag force and velocity of the fluid flow around the cube. To ensure accurate results, it is essential to consider the following:
- Test conditions: The test conditions, such as temperature and humidity, can affect the drag coefficient.
- Cube size and shape: The size and shape of the cube can impact the drag coefficient, so it is crucial to use a representative model.
- Data analysis: Careful data analysis is necessary to extract the drag coefficient from the experimental results.
What is the formula for drag flow?

The formula for drag flow is a mathematical representation of the relationship between the drag force experienced by an object and its velocity, density of the fluid it is moving through, and the shape and size of the object. The formula is given by: Fd = ½ ρ v^2 Cd A, where Fd is the drag force, ρ is the density of the fluid, v is the velocity of the object, Cd is the drag coefficient, and A is the cross-sectional area of the object.
Understanding the Drag Coefficient
The drag coefficient (Cd) is a dimensionless quantity that depends on the shape and size of the object. It is a measure of the aerodynamic or hydrodynamic efficiency of the object. The value of Cd can range from 0.1 for a sphere to 1.3 for a flat plate. The drag coefficient is influenced by factors such as the Reynolds number, Mach number, and the surface roughness of the object. Some key points to note about the drag coefficient are:
- The drag coefficient is a function of the object's shape and size.
- The drag coefficient is influenced by the Reynolds number and Mach number.
- A lower drag coefficient indicates a more aerodynamically efficient shape.
Factors Affecting Drag Flow
Several factors can affect the drag flow, including the velocity of the object, the density of the fluid, and the shape and size of the object. The velocity of the object is a key factor, as it directly affects the magnitude of the drag force. The density of the fluid also plays a crucial role, as it affects the inertia of the fluid and the resulting drag force. Other factors such as turbulence and surface roughness can also influence the drag flow. Key factors affecting drag flow include:
- Velocity of the object.
- Density of the fluid.
- Shape and size of the object.
Applications of Drag Flow Formula
The drag flow formula has numerous applications in various fields, including aerospace engineering, mechanical engineering, and civil engineering. In aerospace engineering, the drag flow formula is used to calculate the drag force experienced by aircraft and spacecraft. In mechanical engineering, the formula is used to design more efficient pumps and turbines. In civil engineering, the formula is used to calculate the drag force experienced by bridges and buildings. Some key applications of the drag flow formula are:
- Aerospace engineering: calculating drag force on aircraft and spacecraft.
- Mechanical engineering: designing efficient pumps and turbines.
- Civil engineering: calculating drag force on bridges and buildings.
Limitations of the Drag Flow Formula
The drag flow formula has several limitations, including its assumption of a laminar flow and its inability to account for turbulence and separation. The formula also assumes a constant density and constant velocity, which may not always be the case in real-world applications. Additionally, the formula does not account for surface roughness and compressibility effects. Some key limitations of the drag flow formula are:
- Assumes laminar flow.
- Does not account for turbulence and separation.
- Assumes constant density and constant velocity.
Modern Developments in Drag Flow Research
Research in drag flow is ongoing, with a focus on developing more accurate and robust models that can account for complex flow phenomena. Computational fluid dynamics (CFD) is being used to simulate turbulent flows and separation. Experimental techniques such as particle image velocimetry (PIV) and laser Doppler velocimetry (LDV) are being used to measure flow velocities and turbulence. Some key areas of research in drag flow include:
- Developing more accurate models for turbulent flows.
- Using CFD to simulate complex flow phenomena.
- Experimental techniques for measuring flow velocities and turbulence.
Frequently Asked Questions (FAQs)
What is Cube Flow Perpendicular to Face Surface Drag and how does it affect the Drag Coefficient Equation?
The Cube Flow Perpendicular to Face Surface Drag is a phenomenon that occurs when a fluid flows perpendicular to the face of a cube, resulting in a significant increase in drag force. This is due to the fact that the cube's face creates a large surface area that is exposed to the fluid flow, leading to a higher resistance to motion. As a result, the drag coefficient equation must take into account this increased resistance when calculating the drag force. The drag coefficient equation is a mathematical formula that is used to calculate the drag force on an object, and it is typically expressed as a function of the object's velocity, density, and surface area. In the case of a cube, the drag coefficient equation must be modified to account for the perpendicular flow and the resulting increase in drag force.
How does the Drag Coefficient Equation change when calculating Cube Flow Perpendicular to Face Surface Drag?
When calculating the drag force on a cube, the drag coefficient equation must be modified to account for the perpendicular flow. This is typically done by introducing a correction factor that takes into account the increased surface area and resistance created by the cube's face. The correction factor is usually a function of the Reynolds number, which is a dimensionless quantity that characterizes the nature of the fluid flow. By incorporating this correction factor into the drag coefficient equation, engineers can accurately calculate the drag force on a cube, even when the flow is perpendicular to its face. The resulting drag coefficient equation is a more complex formula that takes into account the cube's geometry and the fluid properties, allowing for more accurate predictions of the drag force.
What are the key factors that affect the Drag Coefficient Equation when calculating Cube Flow Perpendicular to Face Surface Drag?
The key factors that affect the drag coefficient equation when calculating cube flow perpendicular to face surface drag are the cube's geometry, the fluid properties, and the flow conditions. The cube's geometry plays a crucial role in determining the drag force, as the surface area and shape of the cube can significantly impact the flow resistance. The fluid properties, such as density and viscosity, also affect the drag force, as they determine the flow behavior and resistance. Finally, the flow conditions, including the velocity and Reynolds number, must also be considered when calculating the drag force. By taking into account these key factors, engineers can develop an accurate drag coefficient equation that can be used to predict the drag force on a cube in a variety of flow scenarios.
How can the Cube Flow Perpendicular to Face Surface Drag Calculator be used to simplify the calculation of the Drag Coefficient Equation?
The Cube Flow Perpendicular to Face Surface Drag Calculator is a tool that can be used to simplify the calculation of the drag coefficient equation. This calculator takes into account the cube's geometry, fluid properties, and flow conditions, and uses these inputs to calculate the drag force and drag coefficient. By using this calculator, engineers can quickly and easily calculate the drag force on a cube, without having to manually solve the complex drag coefficient equation. The calculator can also be used to iterate on different design scenarios, allowing engineers to optimize the cube's geometry and flow conditions to minimize the drag force. Additionally, the calculator can be used to validate the results of computational fluid dynamics (CFD) simulations, providing an independent check on the accuracy of the drag force calculations. Overall, the Cube Flow Perpendicular to Face Surface Drag Calculator is a powerful tool that can be used to simplify the calculation of the drag coefficient equation and improve the accuracy of drag force predictions.
Deja una respuesta

Entradas Relacionadas