Converting Sound Power to Sound Pressure Formulas and Calculator

Sound power and sound pressure are two fundamental concepts in acoustics, measuring the energy and intensity of sound waves. Converting between these two quantities is crucial in various fields, including engineering, architecture, and environmental science. The conversion process involves understanding the relationship between sound power, sound pressure, and other factors like frequency and distance. This article provides a comprehensive overview of the formulas and calculations required to convert sound power to sound pressure, along with a calculator to simplify the process and ensure accurate results in real-world applications. Formulas and examples are included for reference.
- Converting Sound Power to Sound Pressure Formulas and Calculator
- How to calculate sound pressure from sound power?
- What is the formula for calculating SPL?
- What is the relationship between sound pressure and sound power?
- How to convert SPL to dB?
-
Frequently Asked Questions (FAQs)
- What is the difference between sound power and sound pressure, and why is it important to convert between them?
- How do I use the sound power to sound pressure conversion formulas and calculator to determine the sound pressure level at a given distance from a source?
- What are the limitations and assumptions of the sound power to sound pressure conversion formulas and calculator, and how can they be overcome?
- Can I use the sound power to sound pressure conversion formulas and calculator to predict the sound pressure level in a reverberant room or a non-uniform environment, and what are the challenges and considerations?
Converting Sound Power to Sound Pressure Formulas and Calculator
Converting sound power to sound pressure is a fundamental concept in acoustics, as it allows us to quantify the intensity of sound in different environments. The sound power of a source is a measure of the total energy emitted by the source, while the sound pressure is a measure of the pressure fluctuations in the air caused by the sound wave. To convert sound power to sound pressure, we need to use specific formulas and calculators.
Understanding Sound Power and Sound Pressure
Sound power and sound pressure are two related but distinct concepts. Sound power is typically measured in watts (W) and represents the total energy emitted by a source, while sound pressure is measured in pascals (Pa) and represents the pressure fluctuations in the air. The relationship between sound power and sound pressure is complex, as it depends on the frequency and distance from the source.
Formulas for Converting Sound Power to Sound Pressure
There are several formulas available to convert sound power to sound pressure, depending on the specific application and conditions. One commonly used formula is the sound power to sound pressure level formula, which is given by: Lp = 10 log10(P / Pr), where Lp is the sound pressure level, P is the sound power, and Pr is the reference sound power. Another formula is the sound pressure to sound power formula, which is given by: P = (p^2) / (ρ c), where P is the sound power, p is the sound pressure, ρ is the air density, and c is the speed of sound.
Sound Pressure Level Calculator
A sound pressure level calculator is a tool used to calculate the sound pressure level from a given sound power or sound pressure. These calculators are often available online or in software packages and can be used to perform quick and accurate calculations. The calculator typically requires input of the sound power, distance, and frequency to calculate the sound pressure level.
Applications of Sound Power to Sound Pressure Conversion
The conversion of sound power to sound pressure has numerous applications in various fields, including acoustics, noise control, and audio engineering. For example, in acoustics, sound power to sound pressure conversion is used to predict the sound pressure level in a room or outdoor environment. In noise control, it is used to assess the noise level emitted by a machine or source. In audio engineering, it is used to optimize the sound system design and ensure that the sound pressure level is within safe limits.
Limitations and Assumptions of Sound Power to Sound Pressure Conversion
The conversion of sound power to sound pressure is based on several assumptions and has some limitations. For example, the formulas assume a free field or anechoic environment, which may not always be the case in real-world applications. Additionally, the conversion is sensitive to frequency and distance, which can affect the accuracy of the results. The following table summarizes some of the key parameters and formulas used in sound power to sound pressure conversion:
| Parameter | Unit | Formula |
|---|---|---|
| Sound Power | Watts (W) | P = (p^2) / (ρ c) |
| Sound Pressure | Pascals (Pa) | p = √(P ρ c) |
| Frequency | Hertz (Hz) | f = 1 / T |
| Distance | Meters (m) | r = √((x^2) + (y^2) + (z^2)) |
| Sound Pressure Level | Decibels (dB) | Lp = 10 log10(P / Pr) |
How to calculate sound pressure from sound power?
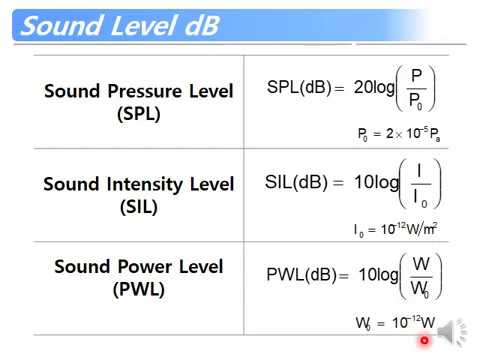
To calculate sound pressure from sound power, we need to understand the relationship between these two quantities. The sound power is a measure of the total energy emitted by a source, while the sound pressure is a measure of the pressure exerted by the sound wave on a surface. The calculation involves the use of the sound power level and the distance from the source to the point where the sound pressure is being measured.
Understanding Sound Power and Sound Pressure
To calculate sound pressure from sound power, it is essential to understand the concepts of sound power and sound pressure. Sound power is typically measured in watts (W) and represents the total energy emitted by a source. On the other hand, sound pressure is measured in pascals (Pa) and represents the pressure exerted by the sound wave on a surface. The relationship between sound power and sound pressure can be described using the following formula:
- The sound power level (Lw) is calculated using the formula Lw = 10log(W/W0), where W is the sound power and W0 is the reference sound power (1 W).
- The sound pressure level (Lp) is calculated using the formula Lp = 20log(p/p0), where p is the sound pressure and p0 is the reference sound pressure (20 μPa).
- The sound pressure can be calculated from the sound power level using the formula p = p0 10^((Lw - 10log(r) - 10.5)/20), where r is the distance from the source to the point where the sound pressure is being measured.
Factors Affecting Sound Pressure Calculation
Several factors can affect the calculation of sound pressure from sound power, including the distance from the source, the frequency of the sound, and the environment in which the sound is being measured. The distance from the source is a crucial factor, as the sound pressure decreases with increasing distance. The frequency of the sound also plays a role, as different frequencies have different sound pressure levels. Additionally, the environment in which the sound is being measured can affect the calculation, as absorption and reflection of sound can occur.
- The distance from the source is a critical factor, as the sound pressure decreases with increasing distance.
- The frequency of the sound also affects the calculation, as different frequencies have different sound pressure levels.
- The environment in which the sound is being measured can also impact the calculation, as absorption and reflection of sound can occur.
Calculating Sound Pressure Level
The sound pressure level (Lp) is a logarithmic measure of the sound pressure and is typically measured in decibels (dB). The calculation of sound pressure level involves the use of the sound power level and the distance from the source to the point where the sound pressure is being measured. The formula for calculating sound pressure level is Lp = Lw - 10log(r) - 10.5, where Lw is the sound power level and r is the distance from the source.
- The sound power level (Lw) is calculated using the formula Lw = 10log(W/W0), where W is the sound power and W0 is the reference sound power (1 W).
- The distance from the source (r) is used to calculate the sound pressure level, as the sound pressure decreases with increasing distance.
- The sound pressure level can be calculated using the formula Lp = Lw - 10log(r) - 10.5.
Applications of Sound Pressure Calculation
The calculation of sound pressure from sound power has several practical applications in various fields, including acoustics, noise control, and audio engineering. In acoustics, the calculation of sound pressure is used to design and optimize acoustic systems, such as loudspeakers and microphones. In noise control, the calculation of sound pressure is used to assess and mitigate noise pollution. In audio engineering, the calculation of sound pressure is used to optimize audio systems and ensure high-quality sound.
- The calculation of sound pressure is used in acoustics to design and optimize acoustic systems.
- The calculation of sound pressure is used in noise control to assess and mitigate noise pollution.
- The calculation of sound pressure is used in audio engineering to optimize audio systems and ensure high-quality sound.
Common Mistakes in Sound Pressure Calculation
There are several common mistakes that can be made when calculating sound pressure from sound power, including ignoring the distance from the source, assuming a constant frequency, and neglecting the environment. Ignoring the distance from the source can result in an incorrect calculation of sound pressure, as the sound pressure decreases with increasing distance. Assuming a constant frequency can also result in an incorrect calculation, as different frequencies have different sound pressure levels. Neglecting the environment can also impact the calculation, as absorption and reflection of sound can occur.
- Ignoring the distance from the source can result in an incorrect calculation of sound pressure.
- Assuming a constant frequency can also result in an incorrect calculation, as different frequencies have different sound pressure levels.
- Neglecting the environment can also impact the calculation, as absorption and reflection of sound can occur.
What is the formula for calculating SPL?

The formula for calculating Sound Pressure Level (SPL) is: SPL = 20log10(P/P0), where P is the root mean square (RMS) sound pressure and P0 is the reference sound pressure, typically 20 micropascals (μPa) in air.
Understanding the Formula
The formula for calculating SPL is based on the logarithmic scale, which allows for a wide range of sound pressures to be represented in a more manageable way. The reference pressure (P0) is a standard value that is used as a basis for comparison, and the RMS sound pressure (P) is a measure of the average sound pressure over a given period of time. Some key points to consider when using this formula include:
- The sound pressure must be measured using a microphone or other acoustic sensor that is capable of detecting the sound waves.
- The reference pressure (P0) must be known in order to calculate the SPL.
- The logarithmic scale used in the formula means that a small change in sound pressure can result in a large change in SPL.
Applications of SPL Calculations
SPL calculations have a wide range of practical applications, including noise pollution monitoring, audio engineering, and hearing protection. By calculating the SPL of a given sound, it is possible to determine the potential health risks associated with exposure to that sound, as well as the perceived loudness. Some examples of applications include:
- Noise ordinances, which often specify maximum allowed SPL levels in certain areas.
- Audio equipment, which may be designed to produce a specific SPL level.
- Hearing protection, which may be required in environments where the SPL is elevated.
Factors Affecting SPL Measurements
There are several factors that can affect SPL measurements, including the distance from the sound source, the frequency of the sound, and the acoustic environment. The distance from the sound source can affect the SPL measurement, as sound waves attenuate over distance. Some other factors to consider include:
- The frequency response of the microphone or other acoustic sensor used to measure the sound pressure.
- The background noise level, which can affect the accuracy of the SPL measurement.
- The room acoustics, which can cause echoes and reflections that can affect the SPL measurement.
Instrumentation for SPL Measurements
There are several types of instrumentation that can be used to measure SPL, including sound level meters, microphones, and acoustic sensors. The sound level meter is a common instrument used to measure SPL, and it typically consists of a microphone, a preamplifier, and a display. Some key features of sound level meters include:
- The frequency weighting, which can be set to A-weighting, C-weighting, or flat weighting.
- The time weighting, which can be set to fast, slow, or impulse.
- The display, which can show the SPL level, as well as other acoustic parameters.
Standards and Regulations for SPL
There are several standards and regulations that govern SPL measurements, including OSHA regulations and IEEE standards. The Occupational Safety and Health Administration (OSHA) has established permissible exposure limits (PELs) for SPL, which are designed to protect workers from noise-induced hearing loss. Some key points to consider include:
- The PEL for SPL, which is typically set at 85 decibels (dB) for an 8-hour time-weighted average.
- The action level, which is typically set at 80 dB and requires hearing conservation programs.
- The requirements for hearing protection, which must be provided to workers exposed to elevated SPL levels.
What is the relationship between sound pressure and sound power?
The relationship between sound pressure and sound power is a fundamental concept in acoustics. Sound pressure refers to the pressure fluctuations in the air caused by a sound wave, while sound power refers to the total energy transmitted by the sound wave per unit time. The relationship between these two quantities is based on the fact that sound power is proportional to the square of sound pressure. This means that as sound pressure increases, sound power increases exponentially.
Defining Sound Pressure and Sound Power
The definition of sound pressure and sound power is crucial in understanding their relationship. Sound pressure is measured in terms of pascals (Pa) and represents the pressure difference between the ambient pressure and the pressure caused by the sound wave. Sound power, on the other hand, is measured in watts (W) and represents the total energy transmitted by the sound wave. The key points to consider are:
- The sound pressure level is typically measured using a sound level meter.
- The sound power level is typically calculated using the sound pressure level and the distance from the source.
- The relationship between sound pressure and sound power is affected by the frequency and directivity of the sound wave.
Measuring Sound Pressure and Sound Power
Measuring sound pressure and sound power requires specialized equipment and techniques. Sound level meters are used to measure sound pressure levels, while sound power levels are typically calculated using computer simulations or empirical models. The key considerations are:
- The accuracy of the measurement depends on the quality of the equipment and the conditions of the measurement.
- The distance from the source and the orientation of the measurement device affect the measurement of sound pressure and sound power.
- The frequency range and dynamic range of the measurement equipment must be suitable for the sound being measured.
Theoretical Relationship between Sound Pressure and Sound Power
The theoretical relationship between sound pressure and sound power is based on the wave equation, which describes the propagation of sound waves in a medium. The sound power level is proportional to the square of the sound pressure level, which means that small changes in sound pressure can result in large changes in sound power. The key points to consider are:
- The wave equation describes the relationship between sound pressure and sound power in terms of frequency, wavelength, and medium properties.
- The sound power level is affected by the directivity and radiation pattern of the sound source.
- The sound pressure level is affected by the distance from the source and the absorption of the medium.
Practical Applications of the Relationship between Sound Pressure and Sound Power
The relationship between sound pressure and sound power has numerous practical applications in fields such as acoustics, audio engineering, and noise control. For example, sound pressure levels are used to evaluate the loudness of a sound, while sound power levels are used to evaluate the energy efficiency of a sound source. The key considerations are:
- The sound pressure level is used to evaluate the noise level in a given environment.
- The sound power level is used to evaluate the energy consumption of a sound source.
- The relationship between sound pressure and sound power is used to optimize the design of sound systems and noise control measures.
Challenges and Limitations in Measuring Sound Pressure and Sound Power
Measuring sound pressure and sound power can be challenging due to various limitations and uncertainties. For example, sound pressure measurements can be affected by background noise, while sound power measurements can be affected by diffraction and scattering. The key points to consider are:
- The accuracy of the measurement depends on the quality of the equipment and the conditions of the measurement.
- The distance from the source and the orientation of the measurement device affect the measurement of sound pressure and sound power.
- The frequency range and dynamic range of the measurement equipment must be suitable for the sound being measured.
How to convert SPL to dB?
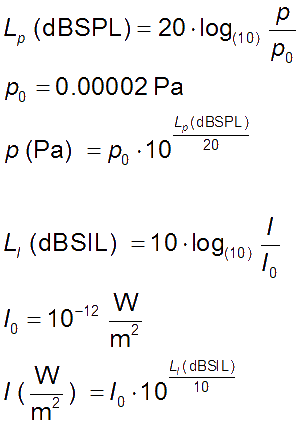
Converting Sound Pressure Level (SPL) to decibels (dB) is a process that involves understanding the relationship between these two units of measurement. The decibel is a unit used to express the ratio of two values of a power or field quantity, whereas SPL is a measure of the sound pressure level. To convert SPL to dB, we use the formula: dB = 20 log10(P/P0), where P is the sound pressure and P0 is the reference sound pressure.
Understanding the Formula
The formula dB = 20 log10(P/P0) is used to calculate the sound pressure level in decibels. This formula involves the logarithm of the ratio of the sound pressure to the reference sound pressure. The reference sound pressure is typically set at 20 micropascals. To apply this formula, we need to know the sound pressure and the reference sound pressure. Here are the steps to follow:
- Determine the sound pressure in pascals.
- Determine the reference sound pressure in pascals.
- Apply the formula dB = 20 log10(P/P0) to calculate the sound pressure level in decibels.
Importance of Reference Sound Pressure
The reference sound pressure is a crucial factor in converting SPL to dB. The reference sound pressure is typically set at 20 micropascals, which is the threshold of human hearing. This value is used as a reference point to calculate the sound pressure level in decibels. The reference sound pressure is important because it provides a standard reference point for comparing different sound pressure levels. Here are the key points to consider:
- The reference sound pressure is set at 20 micropascals.
- This value is used as a reference point to calculate the sound pressure level in decibels.
- The reference sound pressure provides a standard reference point for comparing different sound pressure levels.
Applications of SPL to dB Conversion
The conversion of SPL to dB has several practical applications. One of the main applications is in acoustics, where it is used to measure the sound pressure level of different sounds. This conversion is also used in audio engineering, where it is used to measure the sound pressure level of audio signals. Additionally, this conversion is used in noise pollution studies, where it is used to measure the sound pressure level of different noise sources. Here are the key applications:
- Acoustics: measuring the sound pressure level of different sounds.
- Audio engineering: measuring the sound pressure level of audio signals.
- Noise pollution: measuring the sound pressure level of different noise sources.
Challenges in Converting SPL to dB
Converting SPL to dB can be challenging due to several factors. One of the main challenges is accuracy, as small errors in measurement can result in significant errors in the calculated dB value. Another challenge is units, as the sound pressure must be measured in pascals and the reference sound pressure must be set at 20 micropascals. Here are the key challenges:
- Accuracy: small errors in measurement can result in significant errors in the calculated dB value.
- Units: the sound pressure must be measured in pascals and the reference sound pressure must be set at 20 micropascals.
- Calibration: the equipment used to measure the sound pressure must be calibrated accurately.
Tools and Software for SPL to dB Conversion
There are several tools and software available for converting SPL to dB. One of the main tools is a calculator, which can be used to apply the formula dB = 20 log10(P/P0). Additionally, there are several software programs available that can perform this conversion, such as acoustics software and audio engineering software. Here are the key tools and software:
- Calculator: can be used to apply the formula dB = 20 log10(P/P0).
- Acoustics software: can perform the conversion and provide additional features such as frequency analysis.
- Audio engineering software: can perform the conversion and provide additional features such as signal processing.
Frequently Asked Questions (FAQs)
What is the difference between sound power and sound pressure, and why is it important to convert between them?
The sound power is a measure of the total energy emitted by a source, usually measured in watts (W), while the sound pressure is a measure of the pressure fluctuations in the air caused by the sound wave, typically measured in pascals (Pa) or decibels (dB). Converting between these two quantities is crucial in various fields, such as acoustics, audio engineering, and noise pollution control. The conversion process involves using formulas that take into account the frequency of the sound, the distance from the source, and the characteristics of the surrounding environment. By using these formulas and calculators, professionals can accurately predict and measure the sound pressure levels in a given space, ensuring compliance with regulations and standards for noise exposure.
How do I use the sound power to sound pressure conversion formulas and calculator to determine the sound pressure level at a given distance from a source?
To use the sound power to sound pressure conversion formulas and calculator, you need to know the sound power level of the source, usually expressed in decibels (dB), and the distance from the source to the point where you want to calculate the sound pressure level. The formula involves using the inverse square law, which states that the sound pressure level decreases with the square of the distance from the source. By plugging in the values into the calculator, you can obtain the sound pressure level in decibels (dB) or pascals (Pa). It is essential to consider the directivity of the source, the reflection and absorption of sound by the surrounding surfaces, and the atmospheric conditions, such as temperature and humidity, which can affect the sound propagation. Using the calculator and formulas correctly can help you obtain accurate results and make informed decisions about noise control and acoustic design.
What are the limitations and assumptions of the sound power to sound pressure conversion formulas and calculator, and how can they be overcome?
The sound power to sound pressure conversion formulas and calculator are based on several assumptions and limitations, such as the spherical spreading of sound, the flat frequency response, and the negligible effects of atmospheric absorption and scattering. However, in real-world scenarios, these assumptions may not always hold, and the results may be inaccurate. To overcome these limitations, it is essential to consider the specific characteristics of the source, the environment, and the frequency range of interest. Additionally, using more advanced models, such as the ray tracing or finite element methods, can provide more accurate results, especially in complex and non-uniform environments. Furthermore, measurements and validation of the results using experimental techniques, such as sound level meters or acoustic cameras, can help to verify the accuracy of the calculations and identify potential errors or biases.
Can I use the sound power to sound pressure conversion formulas and calculator to predict the sound pressure level in a reverberant room or a non-uniform environment, and what are the challenges and considerations?
Using the sound power to sound pressure conversion formulas and calculator to predict the sound pressure level in a reverberant room or a non-uniform environment can be challenging due to the complexity of the sound field. In such cases, the assumptions of spherical spreading and flat frequency response may not be valid, and the results may be inaccurate. To overcome these challenges, it is essential to consider the specific characteristics of the room or environment, such as the geometry, materials, and sound absorption properties. Using more advanced models, such as the image source method or ray tracing, can provide more accurate results, especially in complex and non-uniform environments. Additionally, measurements and validation of the results using experimental techniques, such as sound level meters or acoustic cameras, can help to verify the accuracy of the calculations and identify potential errors or biases. It is also important to consider the frequency range of interest and the directivity of the source, as these can significantly affect the sound pressure level in a reverberant room or non-uniform environment.
Deja una respuesta


Entradas Relacionadas