Circular Flat Head with Internal or External Pressure Equation and Calculator

The circular flat head is a critical component in various engineering applications, including pressure vessels, tanks, and pipes. When subjected to internal or external pressure, the flat head must be designed to withstand the resulting stresses to ensure safe and reliable operation. The equation for calculating the stress and required thickness of a circular flat head with internal or external pressure is a complex formula that takes into account the pressure, radius, and material properties. This article provides an overview of the equation and a calculator to simplify the design process. The calculator is easy to use.
-
Circular Flat Head with Internal or External Pressure Equation and Calculator
- Introduction to Circular Flat Head with Internal or External Pressure
- Equation for Circular Flat Head with Internal or External Pressure
- Calculator for Circular Flat Head with Internal or External Pressure
- Material Properties and Geometric Parameters
- Applications of Circular Flat Head with Internal or External Pressure
- What is the formula for the internal pressure of a pressure vessel?
- What is the formula for the internal pressure of a cylinder?
- How to calculate the thickness of a shell?
- How to calculate pressure vessels?
-
Frequently Asked Questions (FAQs)
- What is the significance of the Circular Flat Head with Internal or External Pressure Equation and Calculator in engineering applications?
- How does the Circular Flat Head with Internal or External Pressure Equation and Calculator account for different types of pressure and loading conditions?
- What are the key assumptions and limitations of the Circular Flat Head with Internal or External Pressure Equation and Calculator?
- How can the Circular Flat Head with Internal or External Pressure Equation and Calculator be used in conjunction with other engineering tools and techniques?
Circular Flat Head with Internal or External Pressure Equation and Calculator
The Circular Flat Head with Internal or External Pressure Equation and Calculator is a mathematical tool used to calculate the stress and deflection of a circular flat head under internal or external pressure. This calculator is commonly used in the design and analysis of pressure vessels, pipes, and other cylindrical structures. The equation used to calculate the stress and deflection of the circular flat head is based on the theory of elasticity and thin plate theory.
Introduction to Circular Flat Head with Internal or External Pressure
The circular flat head with internal or external pressure is a common structural element found in many engineering applications. The internal or external pressure applied to the head can cause stress and deflection, which can lead to failure if not properly designed. The calculator uses the formula for the stress and deflection of a circular flat head under internal or external pressure, which is based on the material properties and geometric parameters of the head.
Equation for Circular Flat Head with Internal or External Pressure
The equation for the stress and deflection of a circular flat head under internal or external pressure is given by:
σ = (P r) / (2 t)
where σ is the stress, P is the pressure, r is the radius of the head, and t is the thickness of the head.
Calculator for Circular Flat Head with Internal or External Pressure
The calculator for the circular flat head with internal or external pressure is a simple tool that takes the input values of the pressure, radius, and thickness of the head and calculates the stress and deflection using the equation above. The calculator can be used to design and analyze the circular flat head under internal or external pressure.
Material Properties and Geometric Parameters
The material properties and geometric parameters of the circular flat head are important inputs for the calculator. The material properties include the Young's modulus, Poisson's ratio, and yield strength of the material, while the geometric parameters include the radius, thickness, and diameter of the head.
Applications of Circular Flat Head with Internal or External Pressure
The circular flat head with internal or external pressure has many applications in engineering, including the design and analysis of pressure vessels, pipes, and other cylindrical structures. The calculator can be used to optimize the design of these structures and ensure that they can withstand the internal or external pressure applied to them.
| Parameter | Unit | Description |
|---|---|---|
| Pressure | psi or Pa | The internal or external pressure applied to the head |
| Radius | in or m | The radius of the circular flat head |
| Thickness | in or m | The thickness of the circular flat head |
| Stress | psi or Pa | The stress in the circular flat head due to the internal or external pressure |
| Deflection | in or m | The deflection of the circular flat head due to the internal or external pressure |
What is the formula for the internal pressure of a pressure vessel?
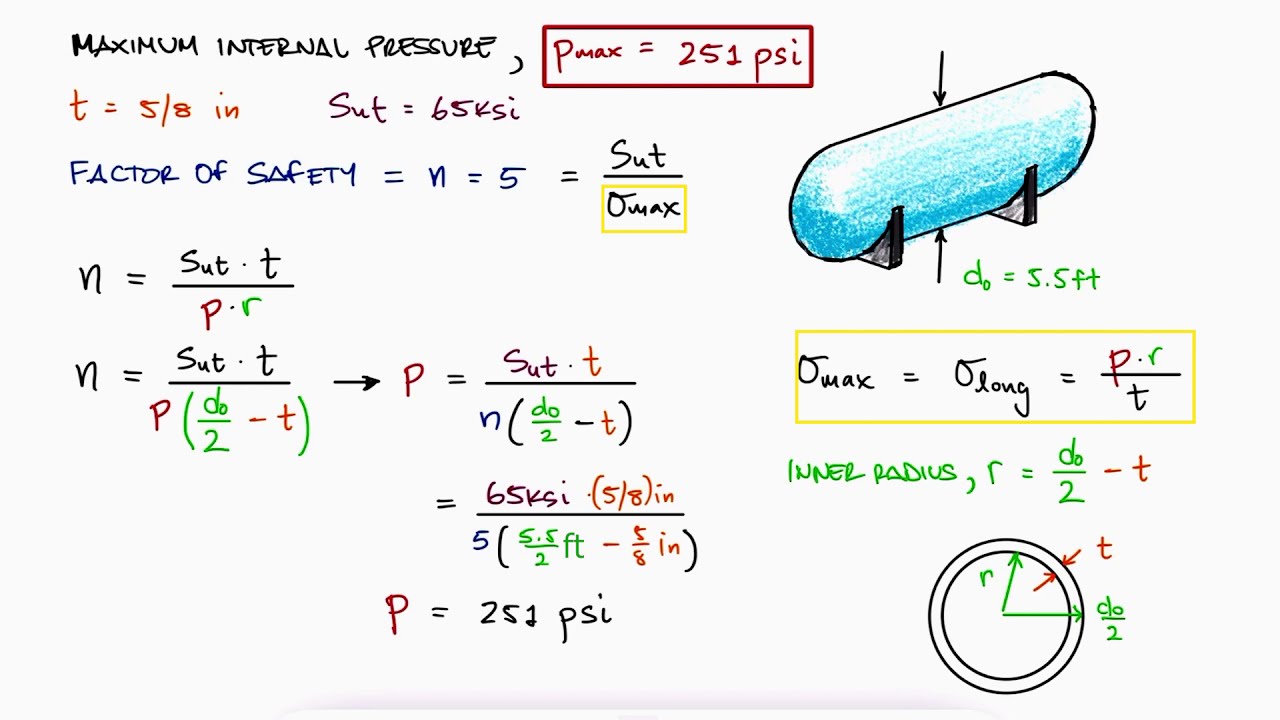
The formula for the internal pressure of a pressure vessel is given by the equation: P = (2 σ t) / r, where P is the internal pressure, σ is the stress at the wall of the vessel, t is the thickness of the wall, and r is the radius of the vessel.
Calculating Internal Pressure
To calculate the internal pressure of a pressure vessel, we need to consider the material properties and the geometrical parameters of the vessel. The stress at the wall of the vessel is a critical factor in determining the internal pressure. The formula P = (2 σ t) / r can be used to calculate the internal pressure, where σ is the allowable stress of the material, t is the thickness of the wall, and r is the radius of the vessel.
- The material properties, such as the yield strength and ultimate strength, are important in determining the stress at the wall of the vessel.
- The geometrical parameters, such as the radius and thickness of the vessel, are also critical in determining the internal pressure.
- The corrosion allowance and weld joint efficiency are also important factors to consider when calculating the internal pressure.
Types of Pressure Vessels
There are different types of pressure vessels, including spherical vessels, cylindrical vessels, and pipeline vessels. Each type of vessel has its own unique design requirements and safety factors. The internal pressure of a pressure vessel can vary depending on the type of vessel and its intended use.
- Spherical vessels are commonly used for storing gases and liquids under high pressure.
- Cylindrical vessels are commonly used for storing gases and liquids under moderate pressure.
- Pipeline vessels are commonly used for transporting gases and liquids under high pressure.
Design and Construction
The design and construction of a pressure vessel are critical in ensuring the safety and reliability of the vessel. The design requirements for a pressure vessel include the material selection, welding procedures, and testing protocols. The construction of a pressure vessel involves the fabrication of the vessel, welding, and testing.
- The material selection is critical in ensuring the strength and durability of the vessel.
- The welding procedures are important in ensuring the integrity of the vessel.
- The testing protocols are critical in ensuring the safety and reliability of the vessel.
Safety Factors
The safety factors of a pressure vessel are critical in ensuring the safety and reliability of the vessel. The safety factors include the corrosion allowance, weld joint efficiency, and testing protocols. The corrosion allowance is a critical factor in determining the thickness of the vessel wall.
- The corrosion allowance is a critical factor in determining the thickness of the vessel wall.
- The weld joint efficiency is important in ensuring the integrity of the vessel.
- The testing protocols are critical in ensuring the safety and reliability of the vessel.
Applications of Pressure Vessels
Pressure vessels have a wide range of applications in various industries, including chemical processing, oil and gas, and power generation. The internal pressure of a pressure vessel can vary depending on the application and intended use.
- Chemical processing applications require pressure vessels that can withstand high temperatures and corrosive environments.
- Oil and gas applications require pressure vessels that can withstand high pressures and corrosive environments.
- Power generation applications require pressure vessels that can withstand high temperatures and high pressures.
What is the formula for the internal pressure of a cylinder?

The formula for the internal pressure of a cylinder is given by the equation P = (2 σ t) / r, where P is the internal pressure, σ is the tensile stress or hoop stress in the cylinder wall, t is the wall thickness, and r is the radius of the cylinder.
Understanding the Formula
The formula for the internal pressure of a cylinder is based on the principle of hoop stress, which states that the stress in a cylindrical vessel is proportional to the internal pressure and the radius of the vessel. This formula is commonly used in the design of pressure vessels, such as pipes, tanks, and cylinders. The key factors that influence the internal pressure of a cylinder are:
- The material properties of the cylinder, such as its tensile strength and yield strength
- The geometry of the cylinder, including its radius and wall thickness
- The internal pressure of the cylinder, which is the pressure exerted by the fluid or gas inside the cylinder
Applications of the Formula
The formula for the internal pressure of a cylinder has a wide range of applications in various fields, including mechanical engineering, chemical engineering, and aerospace engineering. It is used to design and analyze pressure vessels, such as tanks, pipes, and cylinders, that are used to store and transport fluids and gases under high pressure. The key applications of the formula are:
- Design of pressure vessels, including the selection of materials and the determination of dimensions
- Analysis of stress and strain in pressure vessels under various loading conditions
- Safety assessment of pressure vessels, including the evaluation of failure modes and risk assessment
Limitations of the Formula
The formula for the internal pressure of a cylinder has several limitations, including the assumption of thin-walled cylinders and the neglect of end effects. The formula is also based on the theory of elasticity, which assumes that the material behaves elastically under load. The key limitations of the formula are:
- The assumption of thin-walled cylinders, which may not be valid for thick-walled cylinders
- The neglect of end effects, which can influence the stress distribution in the cylinder
- The assumption of elastic behavior, which may not be valid for materials that exhibit non-linear behavior
Derivation of the Formula
The formula for the internal pressure of a cylinder can be derived from the equilibrium equations of a cylindrical shell. The derivation involves the integration of the stress and strain equations over the thickness of the cylinder. The key steps in the derivation are:
- The definition of the stress and strain components in a cylindrical shell
- The equilibrium equations for a cylindrical shell, including the radial and circumferential equilibrium equations
- The integration of the stress and strain equations over the thickness of the cylinder to obtain the formula for the internal pressure
Experimental Verification
The formula for the internal pressure of a cylinder can be verified experimentally using pressure tests and stress measurements. The experimental verification involves the measurement of the internal pressure and the stress distribution in a cylinder under various loading conditions. The key aspects of the experimental verification are:
- The design and fabrication of a test cylinder with instrumentation for pressure and stress measurement
- The performance of pressure tests and stress measurements to verify the formula
- The comparison of the experimental results with the theoretical predictions to validate the formula
How to calculate the thickness of a shell?

To calculate the thickness of a shell, you need to consider the material properties, loading conditions, and design requirements. The thickness of a shell is typically determined using stress analysis and buckling analysis. The shell theory provides a set of equations that describe the behavior of a shell under various loads, including mechanical loads, thermal loads, and pressure loads. By applying these equations, you can determine the required thickness of the shell to ensure its structural integrity and safety.
Understanding Shell Theory
The shell theory is a mathematical framework that describes the behavior of a shell under various loads. To calculate the thickness of a shell, you need to understand the governing equations of shell theory, including the equilibrium equations, compatibility equations, and boundary conditions. The key steps to calculate the thickness of a shell using shell theory are:
- Define the problem geometry and loading conditions
- Determine the material properties, such as Young's modulus and Poisson's ratio
- Apply the shell theory equations to determine the stress resultants and moments
Calculating Stress Resultants
The stress resultants are the forces and moments that act on a shell due to external loads. To calculate the stress resultants, you need to apply the equilibrium equations of shell theory, which involve the in-plane forces, out-of-plane forces, and moments. The key steps to calculate the stress resultants are:
- Determine the in-plane forces, such as normal forces and shear forces
- Calculate the out-of-plane forces, such as transverse shear forces and transverse normal forces
- Apply the equilibrium equations to determine the stress resultants and moments
Determining Material Properties
The material properties play a crucial role in determining the thickness of a shell. The Young's modulus, Poisson's ratio, and yield strength are some of the key material properties that need to be considered. To determine the material properties, you can use experimental methods, such as tensile testing, or numerical methods, such as finite element analysis. The key steps to determine the material properties are:
- Conduct experimental tests to determine the material properties
- Use numerical methods to validate the material properties
- Apply the material properties to the shell theory equations
Applying Buckling Analysis
The buckling analysis is an essential step in determining the thickness of a shell. The buckling load is the critical load at which the shell buckles or deforms excessively. To apply the buckling analysis, you need to use numerical methods, such as finite element analysis, or analytical methods, such as shell theory. The key steps to apply the buckling analysis are:
- Determine the buckling load using numerical methods or analytical methods
- Apply the buckling load to the shell theory equations
- Calculate the required thickness to prevent buckling
Considering Design Requirements
The design requirements play a crucial role in determining the thickness of a shell. The design requirements include the structural integrity, safety, and performance requirements. To consider the design requirements, you need to apply the shell theory equations and buckling analysis to determine the required thickness. The key steps to consider the design requirements are:
- Define the design requirements, such as structural integrity and safety
- Apply the shell theory equations and buckling analysis to determine the required thickness
- Validate the design using experimental methods or numerical methods
How to calculate pressure vessels?

To calculate pressure vessels, you need to consider several factors, including the material properties, dimension of the vessel, and the operating conditions. The calculation involves determining the stress and strain on the vessel walls, which is crucial for ensuring the safety and reliability of the vessel. The calculation process typically starts with determining the design pressure and temperature, followed by calculating the wall thickness and stress using formulas and equations.
Understanding Pressure Vessel Design
To calculate pressure vessels, you need to understand the design principles, including the ASME boiler and pressure vessel code. The design process involves selecting the material that can withstand the operating conditions, determining the dimension of the vessel, and calculating the stress and strain on the vessel walls. The key factors to consider are:
- Material properties: The strength, ductility, and corrosion resistance of the material.
- Dimension: The diameter, length, and wall thickness of the vessel.
- Operating conditions: The temperature, pressure, and fluid properties that the vessel will be exposed to.
Calculating Wall Thickness
Calculating the wall thickness is a critical step in designing a pressure vessel. The wall thickness depends on the design pressure, temperature, and material properties. The calculation involves using formulas and equations to determine the minimum wall thickness required to withstand the operating conditions. The key factors to consider are:
- Design pressure: The maximum pressure that the vessel will be exposed to.
- Temperature: The maximum temperature that the vessel will be exposed to.
- Material properties: The strength, ductility, and corrosion resistance of the material.
Determining Stress and Strain
Determining the stress and strain on the vessel walls is essential for ensuring the safety and reliability of the vessel. The stress and strain depend on the wall thickness, design pressure, and temperature. The calculation involves using formulas and equations to determine the stress and strain on the vessel walls. The key factors to consider are:
- Wall thickness: The minimum wall thickness required to withstand the operating conditions.
- Design pressure: The maximum pressure that the vessel will be exposed to.
- Temperature: The maximum temperature that the vessel will be exposed to.
Considering Safety Factors
Considering safety factors is crucial for ensuring the safety and reliability of the vessel. The safety factors depend on the material properties, design pressure, and temperature. The calculation involves using formulas and equations to determine the safety factors. The key factors to consider are:
- Material properties: The strength, ductility, and corrosion resistance of the material.
- Design pressure: The maximum pressure that the vessel will be exposed to.
- Temperature: The maximum temperature that the vessel will be exposed to.
Using Codes and Standards
Using codes and standards is essential for ensuring the safety and reliability of the vessel. The codes and standards provide guidelines and regulations for designing and manufacturing pressure vessels. The key factors to consider are:
- ASME boiler and pressure vessel code: The standard for designing and manufacturing pressure vessels.
- Material properties: The strength, ductility, and corrosion resistance of the material.
- Design pressure: The maximum pressure that the vessel will be exposed to.
Frequently Asked Questions (FAQs)
What is the significance of the Circular Flat Head with Internal or External Pressure Equation and Calculator in engineering applications?
The Circular Flat Head with Internal or External Pressure Equation and Calculator is a crucial tool in engineering, particularly in the design and analysis of pressure vessels, tanks, and pipes. This equation and calculator help engineers determine the stress and strain on a circular flat head due to internal or external pressure, which is essential for ensuring the safety and integrity of the structure. By using this equation and calculator, engineers can calculate the required thickness of the head, taking into account factors such as material properties, pressure, and temperature. This allows them to design and fabricate safe and efficient structures that can withstand various operating conditions. The calculator is also useful for troubleshooting and optimizing existing designs, as it enables engineers to quickly and accurately simulate different scenarios and predict the behavior of the structure under various loads.
How does the Circular Flat Head with Internal or External Pressure Equation and Calculator account for different types of pressure and loading conditions?
The Circular Flat Head with Internal or External Pressure Equation and Calculator takes into account various types of pressure and loading conditions, including internal pressure, external pressure, axial loads, and bending moments. The equation and calculator consider the effects of these loads on the stress and strain of the circular flat head, allowing engineers to design and analyze structures that are subject to complex loading conditions. For example, in the case of internal pressure, the calculator can account for the hoop stress and longitudinal stress caused by the pressure, as well as the effects of corrosion and erosion on the material properties. Similarly, for external pressure, the calculator can account for the collapse and buckling of the structure due to the pressure, as well as the effects of external loads such as wind and seismic forces. By considering these different types of pressure and loading conditions, the equation and calculator provide a comprehensive and accurate analysis of the circular flat head.
What are the key assumptions and limitations of the Circular Flat Head with Internal or External Pressure Equation and Calculator?
The Circular Flat Head with Internal or External Pressure Equation and Calculator is based on several key assumptions and limitations, including the assumption of a circular and flat head, uniform material properties, and linear elastic behavior. The calculator also assumes that the loading conditions are static and steady-state, and that the structure is free from defects and imperfections. Additionally, the calculator has limitations in terms of its applicability to complex geometries and non-linear material behavior. For example, the calculator may not be suitable for irregularly shaped heads or materials that exhibit non-linear elastic or plastic behavior. Furthermore, the calculator may not account for dynamical loading conditions, such as impact or cyclic loads, which can affect the fatigue and durability of the structure. By understanding these assumptions and limitations, engineers can use the equation and calculator effectively and accurately.
How can the Circular Flat Head with Internal or External Pressure Equation and Calculator be used in conjunction with other engineering tools and techniques?
The Circular Flat Head with Internal or External Pressure Equation and Calculator can be used in conjunction with other engineering tools and techniques, such as finite element analysis (FEA), computational fluid dynamics (CFD), and failure mode and effects analysis (FMEA). By integrating the calculator with these tools, engineers can perform a comprehensive analysis of the circular flat head, including stress, strain, and deformation analysis, as well as fluid flow and heat transfer analysis. For example, FEA can be used to model the behavior of the structure under complex loading conditions, while CFD can be used to simulate the flow of fluids and gases through the structure. Additionally, FMEA can be used to identify and evaluate potential failure modes and effects of the structure, allowing engineers to design and optimize the structure for reliability and safety. By using the calculator in conjunction with these tools, engineers can gain a deeper understanding of the behavior of the circular flat head and design and optimize structures that are safe, efficient, and reliable.
Deja una respuesta

Entradas Relacionadas