Fastener Thermal Expansion Equation and Calculator
Thermal expansion is a critical factor in the design and application of fasteners, as it can significantly impact their performance and integrity. The Fastener Thermal Expansion Equation and Calculator provide a reliable means of calculating the expansion and contraction of fasteners due to temperature changes. This equation takes into account the material properties and temperature range, allowing engineers to accurately predict and compensate for thermal effects, ensuring the safe and efficient operation of mechanical systems and structures. Accurate calculations are essential to prevent failure and maintain system reliability.
- Understanding the Fastener Thermal Expansion Equation and Calculator
- What is the formula for calculating thermal expansion?
- What is the thermal expansion of a bolt?
- What is the linear equation for CTE?
-
Frequently Asked Questions (FAQs)
- What is the Fastener Thermal Expansion Equation and Calculator?
- How does the Fastener Thermal Expansion Equation and Calculator work?
- What are the benefits of using the Fastener Thermal Expansion Equation and Calculator?
- How can I apply the results of the Fastener Thermal Expansion Equation and Calculator to my design?
Understanding the Fastener Thermal Expansion Equation and Calculator
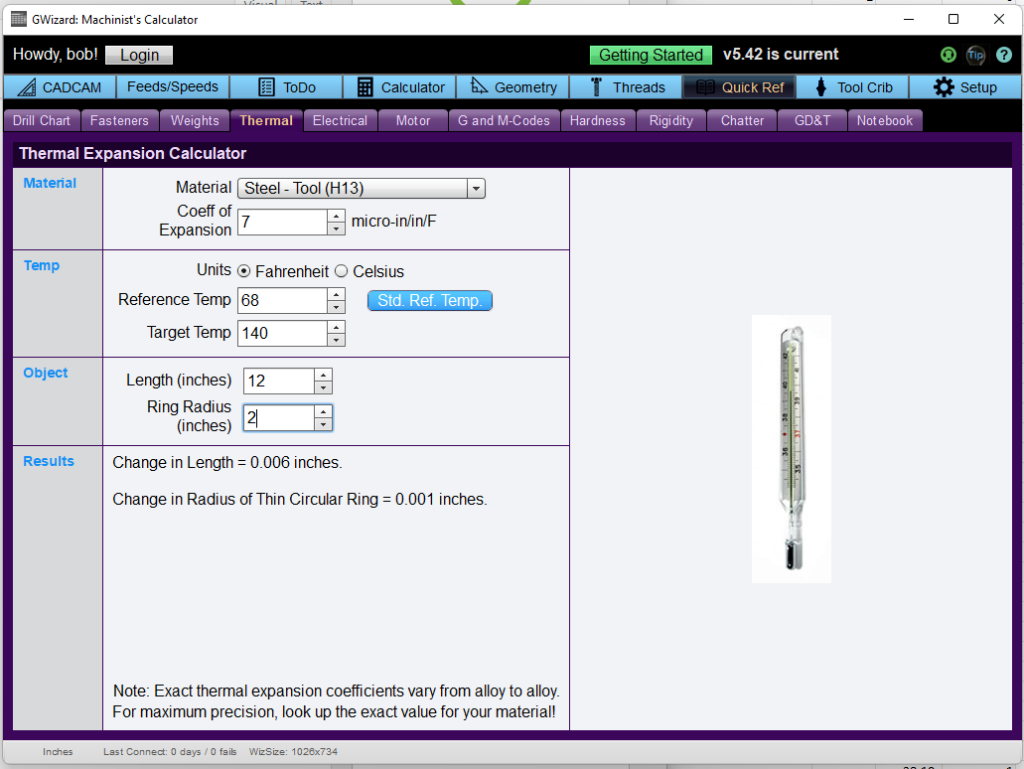
The Fastener Thermal Expansion Equation and Calculator is a tool used to calculate the thermal expansion of fasteners, such as bolts and screws, due to changes in temperature. This is an important consideration in engineering design, as thermal expansion can affect the performance and reliability of mechanical systems. The equation takes into account the coefficient of thermal expansion, temperature change, and initial length of the fastener to calculate the change in length.
Introduction to Thermal Expansion
Thermal expansion is the tendency of a material to change its shape, area, or volume in response to a change in temperature. This phenomenon occurs because the atoms or molecules of the material move faster and spread out as the temperature increases, causing the material to expand. In the context of fasteners, thermal expansion can lead to a change in the length or diameter of the fastener, which can affect the tightness or looseness of the joint.
Fastener Thermal Expansion Equation
The Fastener Thermal Expansion Equation is given by: ΔL = α L ΔT, where ΔL is the change in length, α is the coefficient of thermal expansion, L is the initial length, and ΔT is the temperature change. This equation can be used to calculate the thermal expansion of a fastener, given the material properties and temperature conditions.
Calculator for Fastener Thermal Expansion
A calculator for fastener thermal expansion can be used to simplify the calculation process. The calculator typically takes into account the material type, initial length, temperature change, and coefficient of thermal expansion to calculate the change in length. The calculator can be in the form of a spreadsheet, software, or online tool, and can be used to perform quick calculations and iterations.
Material Properties and Thermal Expansion
The material properties of the fastener, such as the coefficient of thermal expansion, play a crucial role in determining the thermal expansion of the fastener. Different materials have different coefficients of thermal expansion, which can range from low to high. For example, steel has a relatively low coefficient of thermal expansion, while aluminum has a relatively high coefficient of thermal expansion.
Applications of the Fastener Thermal Expansion Equation and Calculator
The Fastener Thermal Expansion Equation and Calculator has various applications in engineering design, such as in the aerospace, automotive, and construction industries. The equation and calculator can be used to design and optimize mechanical systems, predict the behavior of fasteners under different temperature conditions, and ensure the reliability and performance of mechanical systems.
| Material | Coefficient of Thermal Expansion | Temperature Change | Change in Length |
|---|---|---|---|
| Steel | 12x10^-6/K | 100°C | 0.12mm |
| Aluminum | 23x10^-6/K | 100°C | 0.23mm |
What is the formula for calculating thermal expansion?

The formula for calculating thermal expansion is given by ΔL = αL₀ΔT, where ΔL is the change in length, α is the coefficient of thermal expansion, L₀ is the initial length, and ΔT is the change in temperature.
Understanding Thermal Expansion
Thermal expansion is the tendency of materials to change their shape or size in response to changes in temperature. This phenomenon occurs due to the increased kinetic energy of the particles in the material as the temperature rises. The formula for calculating thermal expansion is essential in understanding how materials behave under different thermal conditions.
- Linear expansion occurs when a material expands or contracts in one dimension.
- Area expansion occurs when a material expands or contracts in two dimensions.
- Volumetric expansion occurs when a material expands or contracts in three dimensions.
Factors Affecting Thermal Expansion
The coefficient of thermal expansion is a critical factor in determining the thermal expansion of a material. This coefficient varies depending on the material properties and the temperature range. Other factors that affect thermal expansion include humidity, pressure, and composition of the material.
- Material properties such as density, elasticity, and conductivity influence thermal expansion.
- Temperature range affects the coefficient of thermal expansion, which can be different at various temperature ranges.
- Compositional changes can alter the thermal expansion behavior of a material.
Applications of Thermal Expansion Formula
The thermal expansion formula has numerous practical applications in various fields, including engineering, architecture, and materials science. It is used to design and manufacture temperature-sensitive components, such as thermostats, thermometers, and heat exchangers.
- Designing temperature control systems requires accurate calculations of thermal expansion.
- Thermal stress analysis is crucial in understanding the behavior of materials under thermal loads.
- Materials selection for high-temperature applications relies heavily on the thermal expansion formula.
Calculating Coefficient of Thermal Expansion
The coefficient of thermal expansion can be calculated using various methods, including experimental techniques and theoretical models. The most common method involves measuring the change in length of a material over a known temperature range.
- Experimental methods involve measuring the change in length or volume of a material.
- Theoretical models use mathematical equations to predict the coefficient of thermal expansion.
- Computer simulations can also be used to calculate the coefficient of thermal expansion.
Limitations and Assumptions
The thermal expansion formula is based on several assumptions and has limitations. It assumes that the material is isotropic and homogeneous, and that the temperature change is uniform. Additionally, the formula only applies to small temperature changes.
- Isotropic materials have the same properties in all directions.
- Homogeneous materials have the same composition throughout.
- Temperature gradients can affect the accuracy of the thermal expansion formula.
What is the thermal expansion of a bolt?
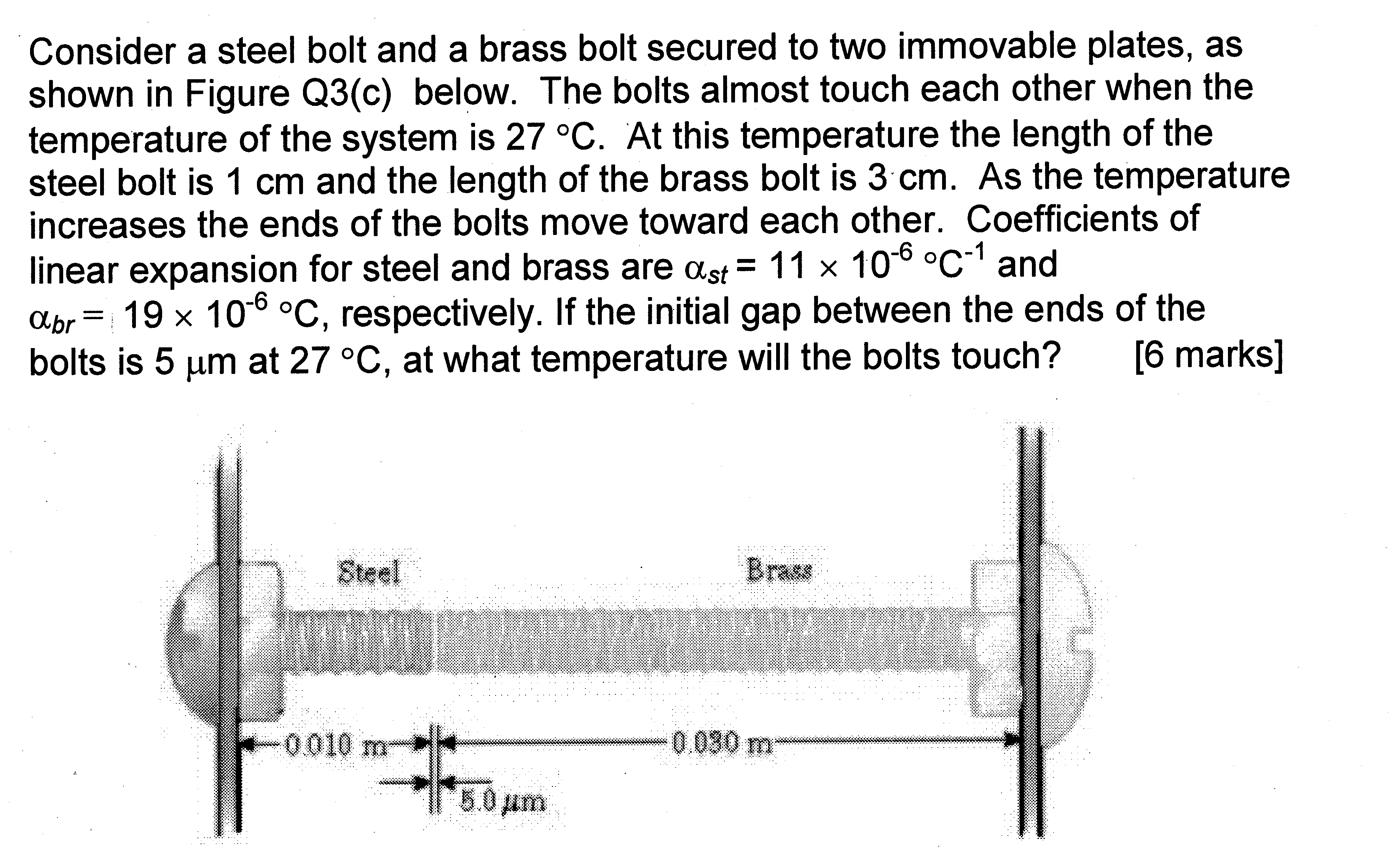
The thermal expansion of a bolt refers to the change in its length or shape due to changes in temperature. This phenomenon occurs because the material of the bolt, typically metal, expands or contracts when it is heated or cooled. The thermal expansion coefficient of the material determines the amount of expansion or contraction that occurs. This coefficient is a measure of how much the material expands or contracts per unit change in temperature.
Factors Affecting Thermal Expansion of Bolts
The thermal expansion of a bolt is affected by several factors, including the material composition, temperature range, and bolt geometry. The thermal expansion coefficient of the material is a critical factor, as it determines the amount of expansion or contraction that occurs. Other factors, such as stress and strain, can also influence the thermal expansion of a bolt. For example:
- The temperature range to which the bolt is exposed can affect its thermal expansion, with higher temperatures resulting in greater expansion.
- The bolt geometry, including its length and diameter, can also impact its thermal expansion, with longer bolts experiencing greater expansion.
- The material composition of the bolt, including its alloy and treatment, can influence its thermal expansion coefficient and overall expansion behavior.
Calculating Thermal Expansion of Bolts
Calculating the thermal expansion of a bolt involves using the thermal expansion coefficient of the material and the temperature change to which the bolt is exposed. The formula for calculating thermal expansion is: ΔL = α L ΔT, where ΔL is the change in length, α is the thermal expansion coefficient, L is the original length, and ΔT is the change in temperature. For example:
- Using the thermal expansion coefficient of the material, which is typically measured in units of 1/K or 1/°C.
- Applying the formula to calculate the change in length of the bolt, taking into account the original length and temperature change.
- Considering other factors, such as stress and strain, that can influence the thermal expansion of the bolt.
Effects of Thermal Expansion on Bolt Performance
The thermal expansion of a bolt can have significant effects on its performance and reliability. For example, excessive expansion can lead to loosening or failure of the bolt, while insufficient expansion can result in over-tightening or galling. The thermal expansion coefficient of the material can also impact the fatigue life of the bolt, with high coefficients resulting in reduced lifespan. For example:
- The thermal expansion of a bolt can affect its clamping force, which can impact the structural integrity of the surrounding material.
- The thermal expansion of a bolt can also influence its corrosion resistance, with expanded bolts being more susceptible to corrosion.
- The thermal expansion of a bolt can impact its reuse, with expanded bolts potentially being damaged or deformed.
Materials with Low Thermal Expansion
Some materials have low thermal expansion coefficients, making them suitable for applications where thermal stability is critical. These materials include invar, kovar, and copper-beryllium alloys, which have thermal expansion coefficients that are significantly lower than those of steel or aluminum. For example:
- Invar has a thermal expansion coefficient of approximately 1.2 x 10^-6 1/K, making it an ideal material for applications where thermal stability is critical.
- Kovar has a thermal expansion coefficient of approximately 5.5 x 10^-6 1/K, making it suitable for applications where thermal expansion must be minimized.
- Copper-beryllium alloys have thermal expansion coefficients that are typically lower than those of steel or aluminum, making them suitable for applications where thermal stability is important.
Design Considerations for Thermal Expansion of Bolts
When designing bolts for thermal expansion, several factors must be considered, including the thermal expansion coefficient of the material, the temperature range to which the bolt will be exposed, and the bolt geometry. The design must also take into account other factors, such as stress and strain, that can influence the thermal expansion of the bolt. For example:
- Selecting a material with a low thermal expansion coefficient to minimize the effects of thermal expansion.
- Designing the bolt geometry to accommodate the thermal expansion, including clearances and tolerances.
- Considering the temperature range to which the bolt will be exposed and designing the bolt accordingly, including insulation and thermal protection.
What is the linear equation for CTE?

The linear equation for CTE (Coefficient of Thermal Expansion) is given by the formula: ΔL = α × L × ΔT, where ΔL is the change in length, α is the coefficient of thermal expansion, L is the original length, and ΔT is the change in temperature. This equation is used to calculate the change in length of a material due to a change in temperature.
Understanding the Concept of CTE
The concept of CTE is crucial in understanding how materials behave under different temperature conditions. The linear equation for CTE is used to predict the change in length of a material, which is essential in various engineering applications. The coefficient of thermal expansion is a measure of how much a material expands or contracts when its temperature changes. Some key points to consider are:
- The CTE value is specific to each material and is usually measured in units of per degree Celsius or Kelvin.
- The CTE value can be positive or negative, depending on whether the material expands or contracts with increasing temperature.
- The linear equation for CTE assumes that the material behaves linearly, meaning that the change in length is directly proportional to the change in temperature.
Applications of the Linear Equation for CTE
The linear equation for CTE has numerous applications in various fields, including engineering, physics, and materials science. The equation is used to design and analyze systems that are subject to temperature changes, such as bridges, buildings, and electronic components. Some key applications are:
- Thermal stress analysis: The linear equation for CTE is used to calculate the thermal stresses that occur in a material due to temperature changes.
- Design of thermal systems: The equation is used to design systems that can withstand temperature changes, such as heat exchangers and thermal interfaces.
- Selection of materials: The CTE value is an important factor in selecting materials for a particular! application, as it can affect the performance and reliability of the system.
Limitations of the Linear Equation for CTE
The linear equation for CTE is a simplified model that assumes a linear relationship between the change in length and the change in temperature. However, in reality, the behavior of materials can be more complex, and the equation may not always be accurate. Some limitations are:
- Non-linear behavior: Some materials exhibit non-linear behavior, meaning that the change in length is not directly proportional to the change in temperature.
- Temperature dependence: The CTE value can be temperature-dependent, meaning that it changes with temperature.
- Material anisotropy: The CTE value can be different in different directions, depending on the material's anisotropy.
Experimental Methods for Measuring CTE
The CTE value can be measured using various experimental methods, including dilatometry, interferometry, and thermal mechanical analysis. These methods involve measuring the change in length of a material as a function of temperature. Some key points to consider are:
- Accuracy and precision: The measurement method should be accurate and precise to obtain reliable CTE values.
- Sample preparation: The sample should be prepared carefully to ensure that it is free from defects and has a uniform microstructure.
- Temperature control: The temperature should be controlled carefully to ensure that the measurement is made at a consistent temperature.
Importance of CTE in Materials Selection
The CTE value is an important factor in selecting materials for a particular application, as it can affect the performance and reliability of the system. A material with a high CTE value may be more prone to thermal stress and failure, while a material with a low CTE value may be more stable and reliable. Some key points to consider are:
- Thermal compatibility: The CTE value should be compatible with the thermal expansion of other materials in the system.
- Thermal stress: The CTE value can affect the thermal stress that occurs in a material due to temperature changes.
- Material stability: The CTE value can affect the stability and reliability of a material over time.
Frequently Asked Questions (FAQs)
What is the Fastener Thermal Expansion Equation and Calculator?
The Fastener Thermal Expansion Equation and Calculator is a tool used to calculate the thermal expansion of fasteners, such as bolts and screws, due to changes in temperature. This equation takes into account the coefficient of thermal expansion of the material, the initial temperature, and the final temperature to determine the change in length of the fastener. The calculator is a useful tool for engineers and designers who need to ensure that their designs can withstand thermal stresses and strains caused by temperature fluctuations. By using the Fastener Thermal Expansion Equation and Calculator, users can determine the maximum allowable temperature range for their fasteners and ensure that their designs are safe and reliable.
How does the Fastener Thermal Expansion Equation and Calculator work?
The Fastener Thermal Expansion Equation and Calculator works by using the formula for thermal expansion, which is given by ΔL = α L ΔT, where ΔL is the change in length, α is the coefficient of thermal expansion, L is the initial length, and ΔT is the change in temperature. The calculator takes the user-input values for the initial temperature, final temperature, and coefficient of thermal expansion, and uses these values to calculate the change in length of the fastener. The calculator also takes into account the Units of measurement, such as degrees Celsius or degrees Fahrenheit, to ensure that the calculation is accurate. By using the Fastener Thermal Expansion Equation and Calculator, users can quickly and easily determine the thermal expansion of their fasteners and ensure that their designs are compatible with the operating conditions.
What are the benefits of using the Fastener Thermal Expansion Equation and Calculator?
The Fastener Thermal Expansion Equation and Calculator offers several benefits to users, including increased accuracy and reduced calculation time. By using the calculator, users can quickly and easily determine the thermal expansion of their fasteners, without having to perform complex mathematical calculations. The calculator also helps to reduce errors and improve safety, by ensuring that the thermal expansion of the fastener is taken into account in the design process. Additionally, the Fastener Thermal Expansion Equation and Calculator can be used to optimize designs, by determining the optimum material and dimensions for the fastener, based on the operating conditions. By using the calculator, users can improve the reliability and performance of their designs, and reduce the risk of failure due to thermal stresses and strains.
How can I apply the results of the Fastener Thermal Expansion Equation and Calculator to my design?
The results of the Fastener Thermal Expansion Equation and Calculator can be applied to a design by using the calculated change in length to determine the maximum allowable temperature range for the fastener. This information can then be used to select the optimum material and dimensions for the fastener, based on the operating conditions. The results can also be used to design the fastener and surrounding components, to ensure that they can withstand the thermal stresses and strains caused by temperature fluctuations. Additionally, the results can be used to develop a maintenance schedule, to ensure that the fastener is inspected and replaced as needed, to prevent failure due to thermal degradation. By applying the results of the Fastener Thermal Expansion Equation and Calculator, users can improve the reliability and performance of their designs, and reduce the risk of failure due to thermal stresses and strains.
Deja una respuesta

Entradas Relacionadas