Calculator Moment of Inertia Equation, Section Modulus Equation, Radii of Gyration Equations Channel Sections
The calculation of moment of inertia, section modulus, and radii of gyration is crucial for structural engineers when designing channel sections. These values are essential in determining the flexural and torsional properties of a channel. The moment of inertia equation, section modulus equation, and radii of gyration equations provide a mathematical framework for calculating these properties. By understanding and applying these equations, engineers can ensure the stability and safety of structures that incorporate channel sections, such as beams and columns, in various construction projects. Accurate calculations are vital for optimal design and performance.
- Calculator Moment of Inertia Equation, Section Modulus Equation, Radii of Gyration Equations Channel Sections
-
Understanding the Fundamentals of Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations for Channel Sections
- Calculator Moment of Inertia Equation for Channel Sections
- Section Modulus Equation for Channel Sections
- Radii of Gyration Equations for Channel Sections
- Applications of Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations
- Limitations and Assumptions of Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations
-
Frequently Asked Questions (FAQs)
- What is the Moment of Inertia Equation for a Channel Section and how is it used in engineering applications?
- How is the Section Modulus Equation used to calculate the bending stress of a channel section, and what are its limitations?
- What are the Radii of Gyration Equations for a Channel Section, and how are they used in engineering applications?
- How do the Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations for Channel Sections relate to each other, and what are their applications in engineering design?
Calculator Moment of Inertia Equation, Section Modulus Equation, Radii of Gyration Equations Channel Sections
The calculator moment of inertia equation, section modulus equation, and radii of gyration equations are essential tools in engineering and physics, particularly in the design and analysis of structural elements such as beams, columns, and channels. These equations help engineers and physicists calculate the moment of inertia, section modulus, and radii of gyration of various shapes, including channel sections.
Introduction to Moment of Inertia
The moment of inertia is a measure of an object's resistance to changes in its rotation. It depends on the mass distribution of the object and the axis of rotation. The moment of inertia is calculated using the formula I = ∫r^2 dm, where I is the moment of inertia, r is the distance from the axis of rotation to the infinitesimal mass element dm. In the context of channel sections, the moment of inertia is crucial in determining the bending stiffness and torsional stiffness of the section.
Section Modulus Equation
The section modulus equation is used to calculate the section modulus of a channel section, which is a measure of the section's ability to resist bending. The section modulus is calculated using the formula S = I/y, where S is the section modulus, I is the moment of inertia, and y is the distance from the neutral axis to the extreme fiber. The section modulus is essential in determining the maximum bending stress that a channel section can withstand.
Radii of Gyration Equations
The radii of gyration equations are used to calculate the radii of gyration of a channel section, which are measures of the section's resistance to rotation about a particular axis. The radii of gyration are calculated using the formulas k_x = √(I_x/A) and k_y = √(I_y/A), where k_x and k_y are the radii of gyration about the x-axis and y-axis, respectively, I_x and I_y are the moments of inertia about the x-axis and y-axis, respectively, and A is the cross-sectional area of the section.
Channel Sections and Their Applications
Channel sections are commonly used in construction, mechanical engineering, and other fields due to their high strength-to-weight ratio and ease of fabrication. They are often used as beams, columns, and frames in buildings, bridges, and other structures. The calculator moment of inertia equation, section modulus equation, and radii of gyration equations are essential tools in the design and analysis of these structures.
Calculator Tools and Resources
There are many calculator tools and resources available online that can help engineers and physicists calculate the moment of inertia, section modulus, and radii of gyration of channel sections. These tools often provide pre-built formulas and graphs that can be used to visualize and analyze the results. Some popular calculator tools include moment of inertia calculators, section modulus calculators, and radii of gyration calculators.
| Calculator Tool | Formula | Description |
|---|---|---|
| Moment of Inertia Calculator | I = ∫r^2 dm | Calculates the moment of inertia of a channel section |
| Section Modulus Calculator | S = I/y | Calculates the section modulus of a channel section |
| Radii of Gyration Calculator | k_x = √(I_x/A) and k_y = √(I_y/A) | Calculates the radii of gyration of a channel section |
Understanding the Fundamentals of Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations for Channel Sections
The calculator moment of inertia equation, section modulus equation, and radii of gyration equations are essential for calculating the mechanical properties of channel sections. These equations are used to determine the moment of inertia, section modulus, and radii of gyration, which are critical parameters in designing and analyzing structural members. The moment of inertia is a measure of the resistance to bending and torsion of a structural member, while the section modulus is a measure of the resistance to bending. The radii of gyration are used to calculate the moment of inertia and section modulus.
Calculator Moment of Inertia Equation for Channel Sections
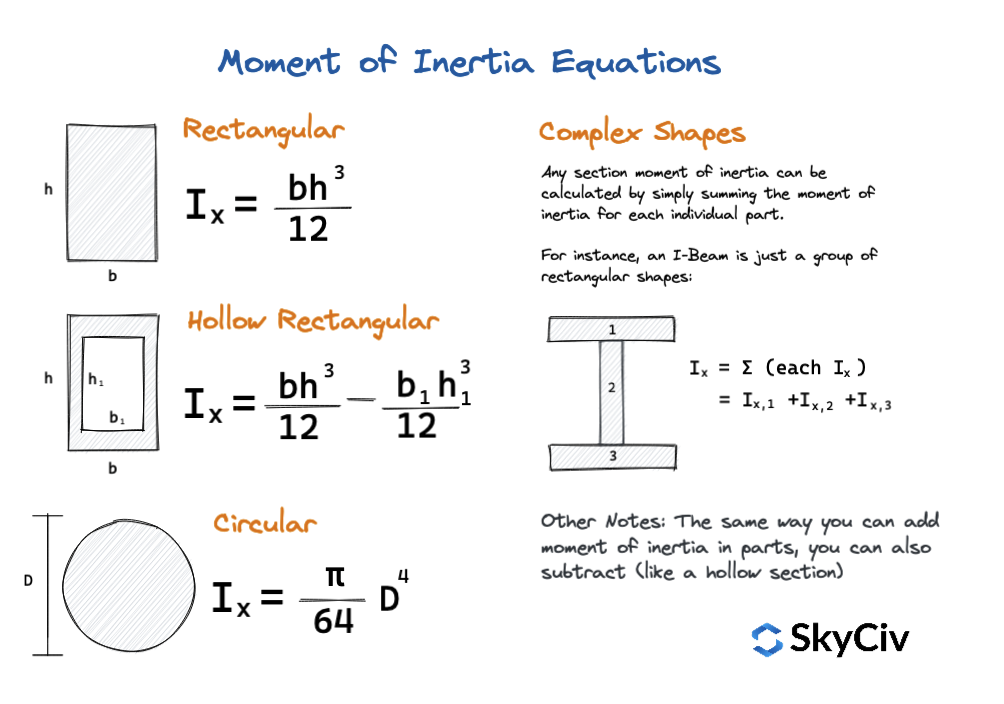
The calculator moment of inertia equation for channel sections is used to calculate the moment of inertia about the x-axis and y-axis. The moment of inertia is calculated using the cross-sectional area and the distance from the axis to the centroid of the section. The equation for the moment of inertia about the x-axis is given by I_x = (b * h^3) / 12, where b is the width of the channel and h is the height of the channel. Similarly, the equation for the moment of inertia about the y-axis is given by I_y = (h * b^3) / 12. These equations are used to calculate the moment of inertia for different types of channel sections, including symmetric and asymmetric channels.
Section Modulus Equation for Channel Sections
The section modulus equation for channel sections is used to calculate the section modulus, which is a measure of the resistance to bending. The section modulus is calculated using the moment of inertia and the distance from the axis to the extreme fiber of the section. The equation for the section modulus is given by S = I / c, where I is the moment of inertia and c is the distance from the axis to the extreme fiber. The section modulus is an important parameter in designing structural members, as it determines the maximum bending stress that a member can withstand.
Radii of Gyration Equations for Channel Sections
The radii of gyration equations for channel sections are used to calculate the radii of gyration, which are used to calculate the moment of inertia and section modulus. The radii of gyration are calculated using the cross-sectional area and the moment of inertia. The equation for the radius of gyration about the x-axis is given by r_x = sqrt(I_x / A), where I_x is the moment of inertia about the x-axis and A is the cross-sectional area. Similarly, the equation for the radius of gyration about the y-axis is given by r_y = sqrt(I_y / A). The radii of gyration are important parameters in designing structural members, as they determine the stability and vibration characteristics of the member.
Applications of Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations
The calculator moment of inertia equation, section modulus equation, and radii of gyration equations have numerous applications in civil engineering, mechanical engineering, and aerospace engineering. These equations are used to design and analyze structural members, such as beams, columns, and frames. They are also used to calculate the mechanical properties of machinery and equipment, such as gears, shafts, and bearings. Additionally, these equations are used to analyze the stability and vibration characteristics of structures and machinery, which is critical in ensuring the safety and reliability of these systems.
Limitations and Assumptions of Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations
The calculator moment of inertia equation, section modulus equation, and radii of gyration equations have several limitations and assumptions that must be considered when using them. One of the main limitations is that these equations assume a homogeneous and isotropic material, which may not be the case in reality. Additionally, these equations assume a linear elastic behavior, which may not be valid for large deformations or nonlinear materials. Furthermore, these equations do not account for boundary conditions, such as supports and loads, which can affect the mechanical properties of the structural member. Therefore, it is essential to carefully evaluate the assumptions and limitations of these equations when using them to design and analyze structural members.
Frequently Asked Questions (FAQs)
What is the Moment of Inertia Equation for a Channel Section and how is it used in engineering applications?
The Moment of Inertia Equation for a channel section is a critical concept in engineering, particularly in the fields of mechanical engineering and civil engineering. The moment of inertia is a measure of an object's resistance to changes in its rotation, and it is essential in calculating the stress and deflection of a beam or a structural member. For a channel section, the moment of inertia equation is given by I = (bh^3)/12 - (bt^3)/12, where b is the width of the channel, h is the height of the channel, and t is the thickness of the channel. This equation is used to calculate the moment of inertia of a channel section around its neutral axis, which is essential in determining the bending stress and deflection of the beam.
How is the Section Modulus Equation used to calculate the bending stress of a channel section, and what are its limitations?
The Section Modulus Equation is used to calculate the bending stress of a channel section, and it is given by S = I/y, where I is the moment of inertia of the channel section and y is the distance from the neutral axis to the extreme fiber of the beam. The section modulus equation is essential in calculating the bending stress of a beam, as it takes into account the non-uniform distribution of stress across the cross-section of the beam. However, the section modulus equation has its limitations, as it assumes that the beam is subjected to pure bending and neglects the effects of shear stress and torsion. Additionally, the section modulus equation is only applicable to beams with a constant cross-section and does not account for variable cross-sections or non-uniform loading.
What are the Radii of Gyration Equations for a Channel Section, and how are they used in engineering applications?
The Radii of Gyration Equations for a channel section are used to calculate the radius of gyration of the channel section around its neutral axis. The radii of gyration equations are given by kx = √(Ix/A) and ky = √(Iy/A), where Ix and Iy are the moments of inertia of the channel section around the x and y axes, respectively, and A is the cross-sectional area of the channel. The radii of gyration equations are essential in calculating the natural frequency of a beam, as they take into account the mass distribution of the beam. The radii of gyration equations are also used in calculating the critical load of a beam, which is the load at which the beam becomes unstable and collapses.
How do the Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations for Channel Sections relate to each other, and what are their applications in engineering design?
The Calculator Moment of Inertia Equation, Section Modulus Equation, and Radii of Gyration Equations for channel sections are all related to each other, as they are used to calculate the mechanical properties of a channel section. The moment of inertia equation is used to calculate the moment of inertia of the channel section, which is then used to calculate the section modulus and radii of gyration. The section modulus equation is used to calculate the bending stress of the beam, while the radii of gyration equations are used to calculate the natural frequency and critical load of the beam. These equations are essential in engineering design, as they are used to calculate the stress, deflection, and stability of a beam or a structural member. They are widely used in the design of buildings, bridges, and machinery, and are an essential tool for engineers and designers to ensure the safety and efficiency of their designs.
Deja una respuesta

Entradas Relacionadas