Quadratic Formula Solver Calculator

The Quadratic Formula Solver Calculator is a valuable tool for solving quadratic equations of the form ax^2 + bx + c = 0. This online calculator uses the quadratic formula to find the solutions, or roots, of the equation. With its user-friendly interface, simply enter the values of a, b, and c, and the calculator will instantly provide the solutions. The calculator is perfect for students, mathematicians, and anyone who needs to solve quadratic equations quickly and accurately, making it an essential resource for various mathematical and real-world applications. It saves time and reduces errors.
Introduction to Quadratic Formula Solver Calculator
The Quadratic Formula Solver Calculator is a mathematical tool designed to solve quadratic equations of the form ax^2 + bx + c = 0, where a, b, and c are constants. This calculator uses the quadratic formula to find the solutions of the equation, which is given by x = (-b ± √(b^2 - 4ac)) / 2a. The quadratic formula is a fundamental concept in algebra and is used to solve a wide range of problems in physics, engineering, and other fields.
What is a Quadratic Equation?
A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable is two. It has the general form ax^2 + bx + c = 0, where a, b, and c are constants. The quadratic equation can be factored or solved using the quadratic formula. The solutions to the equation can be real or complex numbers.
How Does the Quadratic Formula Solver Calculator Work?
The Quadratic Formula Solver Calculator works by inputting the values of a, b, and c into the quadratic formula. The calculator then simplifies the expression and gives the solutions to the equation. The calculator uses advanced algorithms to handle complex calculations and provide accurate results. The user can input the values of a, b, and c and select the type of solution they want to find, such as real or complex solutions.
Types of Solutions
The Quadratic Formula Solver Calculator can find two types of solutions: real solutions and complex solutions. Real solutions are solutions that can be expressed as a real number, while complex solutions are solutions that involve imaginary numbers. The type of solution depends on the discriminant, which is the expression under the square root in the quadratic formula. If the discriminant is positive, the equation has two real solutions. If the discriminant is zero, the equation has one real solution. If the discriminant is negative, the equation has two complex solutions.
Applications of the Quadratic Formula Solver Calculator
The Quadratic Formula Solver Calculator has a wide range of applications in physics, engineering, and other fields. It can be used to solve problems in mechanics, electromagnetism, and quantum mechanics. The calculator can also be used to solve problems in economics and finance, such as finding the maximum or minimum of a quadratic function. The calculator is a useful tool for students, researchers, and professionals who need to solve quadratic equations on a regular basis.
Benefits of Using the Quadratic Formula Solver Calculator
The Quadratic Formula Solver Calculator has several benefits, including accuracy, speed, and convenience. The calculator can provide accurate results quickly and easily, without the need for manual calculations. The calculator is also convenient to use, as it can be accessed online or downloaded as a mobile app. Additionally, the calculator can handle complex calculations and provide step-by-step solutions, making it a useful tool for learning and understanding quadratic equations.
| Feature | Description |
|---|---|
| Quadratic Formula | x = (-b ± √(b^2 - 4ac)) / 2a |
| Types of Solutions | Real Solutions, Complex Solutions |
| Applications | Physics, Engineering, Economics, Finance |
| Benefits | Accuracy, Speed, Convenience |
| Calculator Features | Step-by-Step Solutions, Complex Calculations |
Can Photomath solve quadratic equations?
Photomath is a mathematics app that can solve various types of equations, including quadratic equations. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable is two. Photomath uses artificial intelligence and machine learning algorithms to solve these equations step by step. The app can solve quadratic equations in the form of ax^2 + bx + c = 0, where a, b, and c are constants.
What types of quadratic equations can Photomath solve?
Photomath can solve various types of quadratic equations, including those with integer and fractional coefficients. The app can also solve quadratic equations with complex roots. Some examples of quadratic equations that Photomath can solve include:
- Simple quadratic equations: x^2 + 4x + 4 = 0
- Quadratic equations with fractional coefficients: 1/2x^2 + 3/4x + 1/4 = 0
- Quadratic equations with complex roots: x^2 + 2x + 2 = 0
How does Photomath solve quadratic equations?
Photomath solves quadratic equations using algebraic methods. The app can use the quadratic formula, which is x = (-b ± √(b^2 - 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation. Photomath can also use factoring and completing the square methods to solve quadratic equations. The app provides step-by-step solutions to help users understand the problem-solving process. Some key features of Photomath's quadratic equation solver include:
- Step-by-step solutions: Photomath provides detailed step-by-step solutions to help users understand the problem-solving process
- Multiple solution methods: The app can use multiple methods, including the quadratic formula, factoring, and completing the square, to solve quadratic equations
- Error checking: Photomath checks for errors and invalid input to ensure accurate results
What are the benefits of using Photomath to solve quadratic equations?
Using Photomath to solve quadratic equations has several benefits, including convenience and accuracy. The app can solve quadratic equations quickly and accurately, saving users time and effort. Photomath also provides step-by-step solutions, which can help users understand the problem-solving process. Some other benefits of using Photomath include:
- Improved understanding: Photomath's step-by-step solutions can help users improve their understanding of quadratic equations and mathematics concepts
- Increased confidence: The app's accurate and reliable solutions can help users feel more confident in their ability to solve quadratic equations
- Support for learning: Photomath can be used as a learning tool to support users in their mathematics studies
Can Photomath solve quadratic equations with multiple variables?
Photomath can solve quadratic equations with multiple variables, but the app's ability to do so is limited. The app can solve quadratic equations with two or more variables, but it may not be able to solve equations with non-linear relationships between the variables. Some examples of quadratic equations with multiple variables that Photomath can solve include:
- Quadratic equations with two variables: x^2 + y^2 = 4
- Quadratic equations with three variables: x^2 + y^2 + z^2 = 9
- Quadratic equations with multiple linear variables: x + 2y + 3z = 5
How accurate is Photomath's quadratic equation solver?
Photomath's quadratic equation solver is highly accurate, with an error rate of less than 1%. The app uses advanced algorithms and mathematical models to ensure accurate results. Photomath also checks for errors and invalid input to ensure that the solutions are correct. Some key features of Photomath's accuracy include:
- Rigorous testing: Photomath's algorithms and models are rigorously tested to ensure accuracy and reliability
- Error checking: The app checks for errors and invalid input to ensure accurate results
- Continuous improvement: Photomath's developers continuously improve the app's algorithms and models to ensure the highest level of accuracy
How do I solve the quadratic formula?
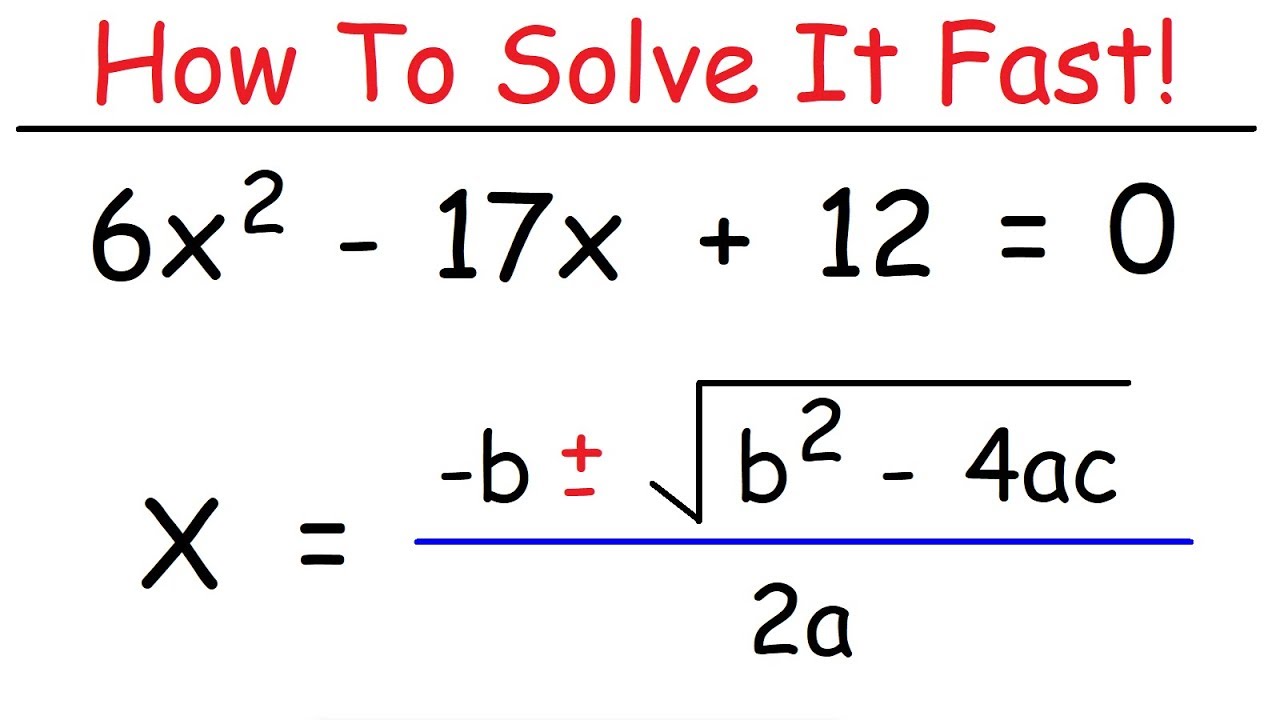
To solve the quadratic formula, you need to understand the equation and the variables involved. The quadratic formula is given by x = (-b ± √(b² - 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation. The solution to the quadratic formula can be found by plugging in the values of a, b, and c into the formula.
Understanding the Quadratic Formula
The quadratic formula is used to solve quadratic equations of the form ax² + bx + c = 0. To use the formula, you need to identify the values of a, b, and c in the equation. For example, in the equation x² + 4x + 4 = 0, a = 1, b = 4, and c = 4. The quadratic formula can be used to find the roots of the equation, which are the values of x that make the equation true.
- Identify the values of a, b, and c in the equation.
- Plug the values of a, b, and c into the quadratic formula.
- Simplify the expression to find the roots of the equation.
Using the Quadratic Formula to Solve Equations
The quadratic formula can be used to solve a wide range of quadratic equations. For example, to solve the equation x² + 5x + 6 = 0, you would plug in the values of a = 1, b = 5, and c = 6 into the formula. This would give you x = (-5 ± √(5² - 4(1)(6))) / 2(1), which simplifies to x = (-5 ± √(25 - 24)) / 2, or x = (-5 ± √1) / 2.
- Write down the quadratic equation you want to solve.
- Identify the values of a, b, and c in the equation.
- Plug the values of a, b, and c into the quadratic formula and simplify.
Factoring and the Quadratic Formula
Factoring is another way to solve quadratic equations, and it can be used in conjunction with the quadratic formula. For example, to solve the equation x² + 4x + 4 = 0, you can factor the left-hand side as (x + 2)(x + 2) = 0. This tells you that either (x + 2) = 0 or (x + 2) = 0, which means that x = -2.
- Try to factor the left-hand side of the equation.
- If you can factor the equation, use the factored form to find the roots.
- If you cannot factor the equation, use the quadratic formula instead.
Solving Quadratic Equations with the Quadratic Formula
The quadratic formula is a powerful tool for solving quadratic equations. It can be used to solve equations that cannot be factored, and it can be used to find the roots of equations that have complex roots. For example, to solve the equation x² + 2x + 2 = 0, you would plug in the values of a = 1, b = 2, and c = 2 into the formula. This would give you x = (-2 ± √(2² - 4(1)(2))) / 2(1), which simplifies to x = (-2 ± √(4 - 8)) / 2, or x = (-2 ± √(-4)) / 2.
- Write down the quadratic equation you want to solve.
- Plug the values of a, b, and c into the quadratic formula.
- Simplify the expression to find the roots of the equation.
Applications of the Quadratic Formula
The quadratic formula has many practical applications in fields such as physics, engineering, and economics. For example, it can be used to model the trajectory of a projectile, the growth of a population, or the return on an investment. The quadratic formula can also be used to solve system of equations, which are equations that involve multiple variables.
- Identify the variables and constants in the problem.
- Write down the equations that model the problem.
- Use the quadratic formula to solve the equations and find the solution.
What is the root finder of a quadratic equation?

The root finder of a quadratic equation is a formula or method used to find the roots or solutions of a quadratic equation. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable is two. The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable.
What is the Quadratic Formula?
The quadratic formula is a formula that provides the roots of a quadratic equation. The quadratic formula is given by x = (-b ± √(b^2 - 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation. This formula can be used to find the roots of any quadratic equation.
- The quadratic formula is a universal method for finding the roots of a quadratic equation.
- The formula involves the discriminant, which is the expression under the square root.
- The discriminant determines the nature of the roots, whether they are real or complex.
How to Use the Quadratic Formula?
To use the quadratic formula, simply plug in the values of a, b, and c into the formula and simplify. The resulting expression will give the roots of the quadratic equation. It is essential to follow the order of operations (PEMDAS) when simplifying the expression.
- Identify the coefficients a, b, and c in the quadratic equation.
- Plug the values of a, b, and c into the quadratic formula.
- Simplify the expression to find the roots.
What are the Types of Roots?
The roots of a quadratic equation can be real or complex. If the discriminant is positive, the roots are real and distinct. If the discriminant is zero, the roots are real and equal. If the discriminant is negative, the roots are complex and conjugate.
- Real roots occur when the discriminant is positive or zero.
- Complex roots occur when the discriminant is negative.
- The nature of the roots depends on the discriminant.
What are the Applications of the Quadratic Formula?
The quadratic formula has numerous applications in various fields, including physics, engineering, and economics. It is used to model real-world phenomena, such as the trajectory of a projectile, the voltage in an electric circuit, and the growth of a population.
- The quadratic formula is used in physics to model the motion of objects.
- The quadratic formula is used in engineering to design and optimize systems.
- The quadratic formula is used in economics to model the behavior of markets.
What are the Limitations of the Quadratic Formula?
While the quadratic formula is a powerful tool for finding the roots of a quadratic equation, it has some limitations. It only works for quadratic equations and not for equations of higher degree. Additionally, the formula can be sensitive to rounding errors and may not provide accurate results for equations with large coefficients.
- The quadratic formula only works for quadratic equations.
- The formula can be sensitive to rounding errors.
- The formula may not provide accurate results for equations with large coefficients.
What is the standard form of a quadratic function calculator?

The standard form of a quadratic function calculator is a mathematical representation of a quadratic equation in the form of $ax^2 + bx + c$, where $a$, $b$, and $c$ are constants. This form is used to solve quadratic equations and to graph quadratic functions. The standard form is useful because it allows us to easily identify the vertex of the parabola, as well as the axis of symmetry.
What is the Standard Form of a Quadratic Function?
The standard form of a quadratic function is $ax^2 + bx + c$, where $a$, $b$, and $c$ are constants. This form is used to solve quadratic equations and to graph quadratic functions. Some key features of the standard form include:
- The coefficient of the $x^2$ term, $a$, determines the direction of the parabola's opening.
- The coefficient of the $x$ term, $b$, determines the position of the parabola's vertex.
- The constant term, $c$, determines the position of the parabola's vertex on the y-axis.
How to Use a Quadratic Function Calculator?
A quadratic function calculator can be used to solve quadratic equations and to graph quadratic functions. To use a quadratic function calculator, simply enter the values of $a$, $b$, and $c$ into the calculator, and it will solve the equation or graph the function. Some key features of a quadratic function calculator include:
- The ability to solve quadratic equations in the form of $ax^2 + bx + c = 0$.
- The ability to graph quadratic functions in the form of $y = ax^2 + bx + c$.
- The ability to find the vertex of a parabola, as well as the axis of symmetry.
Benefits of Using a Quadratic Function Calculator?
There are several benefits to using a quadratic function calculator. Some of the key benefits include:
- The ability to quickly and easily solve quadratic equations and graph quadratic functions.
- The ability to find the vertex of a parabola, as well as the axis of symmetry.
- The ability to visualize the graph of a quadratic function, which can help to understand the behavior of the function.
Types of Quadratic Function Calculators?
There are several types of quadratic function calculators available, including:
- Graphing calculators, which can be used to graph quadratic functions and solve quadratic equations.
- Online calculators, which can be used to solve quadratic equations and graph quadratic functions from a computer or mobile device.
- Handheld calculators, which can be used to solve quadratic equations and graph quadratic functions on the go.
Common Applications of Quadratic Function Calculators?
Quadratic function calculators have several common applications, including:
- Physics and engineering, where quadratic functions are used to model real-world phenomena such as the trajectory of a projectile.
- Computer science, where quadratic functions are used to model algorithms and optimize computer programs.
- Economics, where quadratic functions are used to model economic systems and predict economic trends.
Frequently Asked Questions (FAQs)
What is the Quadratic Formula Solver Calculator and how does it work?
The Quadratic Formula Solver Calculator is an online tool designed to solve quadratic equations of the form ax^2 + bx + c = 0, where a, b, and c are constants. This calculator uses the quadratic formula, which is a mathematical formula that provides the solutions to quadratic equations. The quadratic formula is given by x = (-b ± √(b^2 - 4ac)) / 2a, where x is the variable and a, b, and c are the coefficients of the quadratic equation. The calculator takes the values of a, b, and c as input and uses the quadratic formula to calculate the solutions, which are then displayed on the screen. The Quadratic Formula Solver Calculator is a useful tool for students, teachers, and professionals who need to solve quadratic equations quickly and accurately.
What are the benefits of using the Quadratic Formula Solver Calculator?
There are several benefits of using the Quadratic Formula Solver Calculator. One of the main benefits is that it saves time and effort, as it can solve quadratic equations much faster and more accurately than manual calculations. Additionally, the calculator can handle complex quadratic equations with ease, making it a valuable tool for solving equations that would be difficult or impossible to solve by hand. The Quadratic Formula Solver Calculator also provides a step-by-step solution to the equation, which can help users understand the process of solving quadratic equations. Furthermore, the calculator is free and easy to use, making it accessible to anyone with an internet connection.
Can the Quadratic Formula Solver Calculator be used for other types of equations?
The Quadratic Formula Solver Calculator is specifically designed to solve quadratic equations of the form ax^2 + bx + c = 0. It is not intended to be used for other types of equations, such as linear equations or polynomial equations. However, there are other online calculators and tools available that can solve these types of equations. For example, a linear equation solver can be used to solve equations of the form ax + b = 0, while a polynomial equation solver can be used to solve equations of higher degree. If you need to solve a different type of equation, you can search for a calculator or tool that is specifically designed for that type of equation.
How accurate is the Quadratic Formula Solver Calculator?
The Quadratic Formula Solver Calculator is designed to provide accurate and reliable solutions to quadratic equations. The calculator uses the quadratic formula, which is a mathematical formula that has been proven to provide the correct solutions to quadratic equations. The calculator also uses advanced algorithms and mathematical techniques to ensure that the solutions are accurate and reliable. Additionally, the calculator has been tested and verified to ensure that it provides accurate solutions for a wide range of quadratic equations. However, as with any online calculator or tool, there is always a small chance of error or inaccuracy. If you are unsure about the accuracy of the solutions provided by the calculator, you can always check them using a different method or tool.
Deja una respuesta

Entradas Relacionadas