Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator:

The design and analysis of seamless full-hemispherical head ASME pressure vessels have become increasingly crucial in various industries. These vessels are widely used for storing liquids and gases under high pressure, requiring precise calculations to ensure safety and efficiency. The American Society of Mechanical Engineers (ASME) provides a set of guidelines and equations for the design of such vessels, taking into account factors like material properties, dimensions, and operating conditions. This article will delve into the key equations and provide a calculator for seamless full-hemispherical head ASME pressure vessels, facilitating accurate and reliable designs. Calculations will be explored in detail.
- Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator
- How to calculate hemispherical head?
- What is hemispherical pressure vessel head?
- What is the depth of a hemispherical head?
-
Frequently Asked Questions (FAQs)
- What is the Seamless Full-Hemispherical Head ASME Pressure Vessel and its importance in engineering applications?
- How do the Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator work, and what are their limitations?
- What are the key factors that affect the design and operation of Seamless Full-Hemispherical Head ASME Pressure Vessels, and how can they be optimized?
- How can the Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator be applied to real-world engineering problems, and what are the potential benefits and challenges?
Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator
The Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator are used to calculate the thickness and stress of a seamless full-hemispherical head pressure vessel. The ASME (American Society of Mechanical Engineers) code provides guidelines for the design and construction of pressure vessels, including the calculation of stress and strain on the vessel.
Introduction to Seamless Full-Hemispherical Head ASME Pressure Vessel
A seamless full-hemispherical head is a type of pressure vessel head that is formed from a single piece of metal without any welds or seams. This type of head is often used in high-pressure applications, such as in the petrochemical and nuclear industries, where the integrity of the vessel is critical. The ASME code provides equations and guidelines for the design and calculation of these vessels, including the thickness and stress calculations.
ASME Pressure Vessel Equations
The ASME code provides several equations for calculating the thickness and stress of a seamless full-hemispherical head pressure vessel. These equations take into account the internal pressure, external pressure, and temperature of the vessel, as well as the properties of the material used to construct the vessel. The equations are based on the theory of elasticity and the theory of plasticity, and are used to determine the minimum thickness required for the vessel to withstand the applied loads.
Seamless Full-Hemispherical Head Pressure Vessel Calculator
A calculator is a tool used to perform calculations and determine the thickness and stress of a seamless full-hemispherical head pressure vessel. The calculator uses the ASME equations and guidelines to perform the calculations, and can be used to determine the minimum thickness required for the vessel to withstand the applied loads. The calculator can also be used to determine the stress and strain on the vessel, and to identify any potential weak points in the design.
Advantages of Seamless Full-Hemispherical Head ASME Pressure Vessel
There are several advantages to using a seamless full-hemispherical head ASME pressure vessel, including:
| Advantage | Description |
|---|---|
| Increased Safety | The seamless design eliminates the risk of weld failures and leaks. |
| Improved Durability | The seamless design provides a smooth and consistent surface, reducing the risk of corrosion and wear. |
| Reduced Maintenance | The seamless design reduces the need for weld repairs and maintenance. |
| Increased Efficiency | The seamless design provides a smooth and consistent surface, reducing the risk of energy losses and inefficiencies. |
| Cost-Effective | The seamless design can be more cost-effective than traditional welded designs. |
Applications of Seamless Full-Hemispherical Head ASME Pressure Vessel
Seamless full-hemispherical head ASME pressure vessels are used in a variety of industries, including the petrochemical, nuclear, and chemical industries. They are also used in power generation, water treatment, and food processing applications, where the integrity of the vessel is critical. The vessels are designed to withstand high pressures and temperatures, and are used to store and process hazardous materials.
How to calculate hemispherical head?

To calculate a hemispherical head, you need to understand the formula and the variables involved. The hemispherical head is a type of tank head that is half of a sphere, and its volume can be calculated using the formula: V = (2/3)πr³, where V is the volume and r is the radius of the sphere. To calculate the hemispherical head, you need to know the radius of the sphere and the thickness of the head.
Understanding the Formula
The formula for calculating the hemispherical head is based on the volume of a sphere. The volume of a sphere is given by the formula: V = (4/3)πr³, where V is the volume and r is the radius of the sphere. To calculate the hemispherical head, you need to divide the volume of the sphere by 2, since the hemispherical head is half of a sphere. The formula can be broken down into the following steps:
- Calculate the radius of the sphere
- Calculate the volume of the sphere using the formula: V = (4/3)πr³
- Divide the volume of the sphere by 2 to get the volume of the hemispherical head
Calculating the Radius
The radius of the sphere is a critical variable in calculating the hemispherical head. The radius can be calculated using the diameter of the sphere, which is twice the radius. To calculate the radius, you need to know the diameter of the sphere, which can be measured or calculated using other variables. The radius can be calculated using the following steps:
- Measure or calculate the diameter of the sphere
- Divide the diameter by 2 to get the radius
- Use the radius to calculate the volume of the sphere
Calculating the Volume
The volume of the sphere is a critical variable in calculating the hemispherical head. The volume can be calculated using the formula: V = (4/3)πr³, where V is the volume and r is the radius of the sphere. To calculate the volume, you need to know the radius of the sphere, which can be calculated using the diameter. The volume can be calculated using the following steps:
- Calculate the radius of the sphere
- Use the formula: V = (4/3)πr³ to calculate the volume
- Divide the volume by 2 to get the volume of the hemispherical head
Calculating the Thickness
The thickness of the hemispherical head is a critical variable in calculating its weight and strength. The thickness can be calculated using the formula: t = (P r) / (2 σ), where t is the thickness, P is the pressure, r is the radius, and σ is the stress. To calculate the thickness, you need to know the pressure, radius, and stress of the hemispherical head. The thickness can be calculated using the following steps:
- Calculate the pressure of the hemispherical head
- Calculate the radius of the sphere
- Use the formula: t = (P r) / (2 σ) to calculate the thickness
Applying the Calculations
The calculations for the hemispherical head can be applied in various fields, such as engineering, architecture, and design. The calculations can be used to determine the weight, strength, and stability of the hemispherical head. To apply the calculations, you need to know the variables involved, such as the radius, thickness, and pressure. The calculations can be applied using the following steps:
- Calculate the radius and thickness of the hemispherical head
- Calculate the volume and weight of the hemispherical head
- Use the calculations to determine the strength and stability of the hemispherical head
What is hemispherical pressure vessel head?
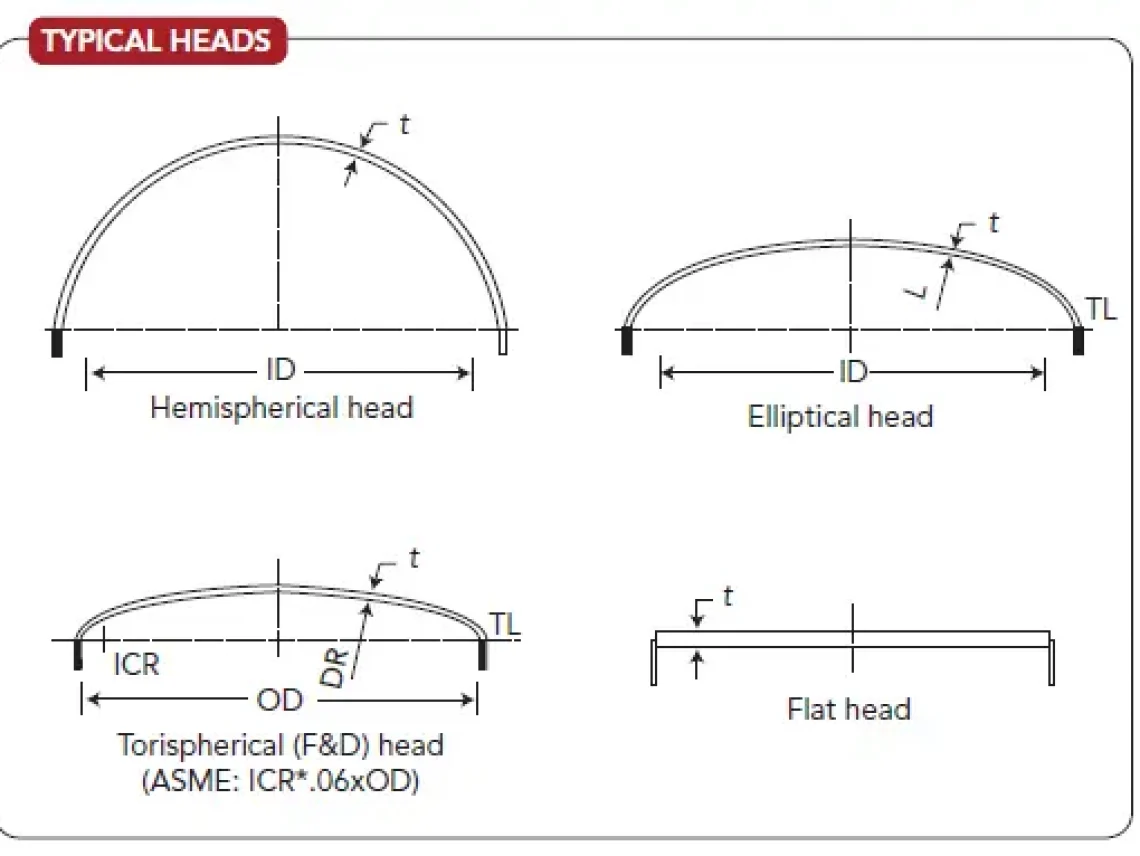
A hemispherical pressure vessel head is a type of curved surface used to enclose the end of a pressure vessel, which is a container designed to hold gases or liquids at a pressure higher than the surrounding environment. The hemispherical shape provides a strong and efficient way to distribute the stress caused by the internal pressure, making it a popular choice for many industrial applications.
Design and Fabrication
The design and fabrication of a hemispherical pressure vessel head require careful consideration of the material properties and the design specifications. The head is typically made from a single piece of metal or composite material, which is formed into a hemispherical shape using various techniques such as spinning, forging, or welding. The thickness of the head is critical in determining its ability to withstand the internal pressure, and it is often calculated using finite element analysis or other numerical methods. Some of the key factors to consider in the design and fabrication of a hemispherical pressure vessel head include:
- Material selection: choosing a material that can withstand the operating temperature and pressure conditions
- Thickness calculation: calculating the minimum required thickness to ensure the head can withstand the internal pressure
- Forming and fabrication: selecting a suitable forming and fabrication method to create the hemispherical shape
Advantages and Benefits
The use of a hemispherical pressure vessel head offers several advantages and benefits over other types of heads. One of the main advantages is the high stress resistance provided by the hemispherical shape, which allows for a more efficient use of material. Additionally, the hemispherical head is often less expensive to fabricate than other types of heads, such as elliptical or torispherical heads. Some of the key advantages and benefits of a hemispherical pressure vessel head include:
- High stress resistance: the hemispherical shape provides a high level of resistance to stress and deformation
- Material efficiency: the hemispherical shape allows for a more efficient use of material
- Cost-effectiveness: the hemispherical head is often less expensive to fabricate than other types of heads
Applications and Industries
Hemispherical pressure vessel heads are used in a wide range of applications and industries, including petrochemical, nuclear, and aerospace. They are often used in high-pressure and high-temperature applications, such as reactors, tanks, and piping systems. The corrosion resistance and durability of the hemispherical head make it a popular choice for use in harsh environments. Some of the key applications and industries that use hemispherical pressure vessel heads include:
- Petrochemical industry: used in reactors, tanks, and piping systems
- Nuclear industry: used in reactors and containment vessels
- Aerospace industry: used in fuel tanks and propulsion systems
Testing and Inspection
The testing and inspection of a hemispherical pressure vessel head are critical to ensuring its safety and reliability. The head is typically subject to a range of non-destructive testing methods, including ultrasonic testing, radiographic testing, and magnetic particle testing. The inspection process involves verifying the dimensions, thickness, and surface finish of the head to ensure it meets the design specifications. Some of the key testing and inspection methods used for hemispherical pressure vessel heads include:
- Ultrasonic testing: used to detect defects and discontinuities in the material
- Radiographic testing: used to inspect the internal structure of the head
- Magnetic particle testing: used to detect surface defects and cracks
Codes and Standards
The design, fabrication, and testing of a hemispherical pressure vessel head are governed by a range of codes and standards, including the ASME Boiler and Pressure Vessel Code and the API Standard 650. These codes and standards provide guidelines and requirements for the design, fabrication, and testing of pressure vessel heads, including the material selection, thickness calculation, and inspection methods. Some of the key codes and standards that apply to hemispherical pressure vessel heads include:
- ASME Boiler and Pressure Vessel Code: provides guidelines for the design and fabrication of boilers and pressure vessels
- API Standard 650: provides guidelines for the design and fabrication of welded steel tanks
- ASTM Standards: provides guidelines for the testing and inspection of materials and components
What is the depth of a hemispherical head?
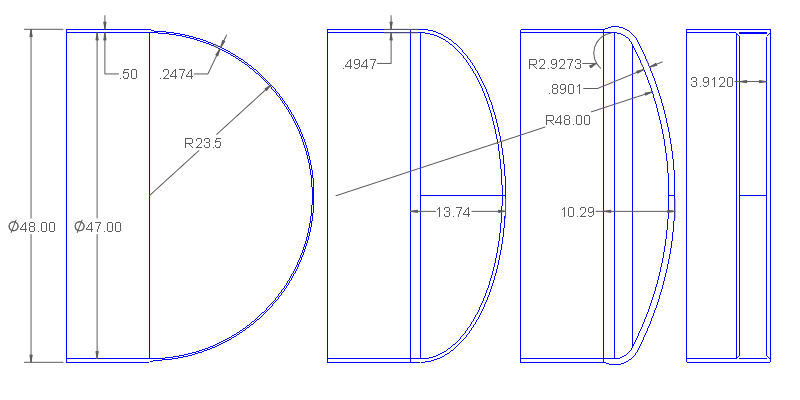
The depth of a hemispherical head is a measure of its curvature, which is typically defined as the distance from the center of the sphere to the edge of the hemisphere. In a hemispherical head, this distance is equal to the radius of the sphere. The depth of a hemispherical head can vary depending on the specific application and design requirements. For example, in pressure vessels, the depth of the hemispherical head is critical in determining the stress and strain on the material.
Introduction to Hemispherical Heads
The hemispherical head is a type of circular head that is commonly used in pressure vessels, tanks, and pipes. The depth of a hemispherical head is an important factor in determining its strength and stability. Some key features of hemispherical heads include:
- Uniform stress distribution: Hemispherical heads are designed to distribute stress evenly across the surface, which helps to prevent failure.
- High pressure resistance: Hemispherical heads are capable of withstanding high pressures, making them suitable for use in pressure vessels and tanks.
- Low weight: Hemispherical heads are often lighter than other types of heads, which can help to reduce the overall weight of the vessel or tank.
Calculating the Depth of a Hemispherical Head
To calculate the depth of a hemispherical head, you need to know the radius of the sphere and the thickness of the material. The depth of the hemispherical head can be calculated using the following formula: depth = radius - thickness. Some key factors to consider when calculating the depth of a hemispherical head include:
- Material properties: The strength and stiffness of the material can affect the depth of the hemispherical head.
- Design requirements: The pressure and temperature requirements of the vessel or tank can impact the depth of the hemispherical head.
- Manufacturing process: The manufacturing process used to create the hemispherical head can also affect its depth and accuracy.
Applications of Hemispherical Heads
Hemispherical heads are used in a variety of applications, including pressure vessels, tanks, and pipes. The depth of the hemispherical head is critical in determining its performance and safety. Some common applications of hemispherical heads include:
- Chemical processing: Hemispherical heads are used in chemical processing equipment, such as reactors and separators.
- Power generation: Hemispherical heads are used in power generation equipment, such as boilers and heat exchangers.
- Oil and gas: Hemispherical heads are used in oil and gas equipment, such as tanks and pipelines.
Advantages of Hemispherical Heads
Hemispherical heads offer several advantages over other types of heads, including uniform stress distribution, high pressure resistance, and low weight. The depth of the hemispherical head is an important factor in determining its strength and stability. Some key advantages of hemispherical heads include:
- Improved safety: Hemispherical heads are designed to withstand high pressures and temperatures, which helps to improve safety.
- Increased efficiency: Hemispherical heads can help to improve efficiency by reducing stress and strain on the material.
- Reduced maintenance: Hemispherical heads are often easier to maintain than other types of heads, which can help to reduce downtime and costs.
Design Considerations for Hemispherical Heads
When designing a hemispherical head, there are several factors to consider, including material properties, design requirements, and manufacturing process. The depth of the hemispherical head is critical in determining its performance and safety. Some key design considerations for hemispherical heads include:
- Material selection: The material used to create the hemispherical head must be able to withstand the pressure and temperature requirements of the application.
- Thickness calculation: The thickness of the hemispherical head must be calculated carefully to ensure that it can withstand the stress and strain of the application.
- Welding and fabrication: The welding and fabrication process used to create the hemispherical head must be carefully controlled to ensure accuracy and quality.
Frequently Asked Questions (FAQs)
What is the Seamless Full-Hemispherical Head ASME Pressure Vessel and its importance in engineering applications?
The Seamless Full-Hemispherical Head ASME Pressure Vessel is a type of pressure vessel that is designed to withstand high internal pressures. It is a crucial component in various industrial applications, including chemical processing, power generation, and oil and gas production. The seamless full-hemispherical head design provides a high level of structural integrity and safety, making it an ideal choice for applications where high-pressure and high-temperature conditions are involved. The ASME (American Society of Mechanical Engineers) code provides a set of standards and guidelines for the design, fabrication, and testing of pressure vessels, ensuring that they meet the required safety and performance criteria.
How do the Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator work, and what are their limitations?
The Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator are used to determine the wall thickness and stress levels in a pressure vessel. The equations take into account various design parameters, such as the internal pressure, temperature, and material properties, to calculate the required wall thickness and stress levels. The calculator provides a user-friendly interface to input the design parameters and calculate the results. However, the equations and calculator have certain limitations, such as assuming a perfectly spherical shape and neglecting non-uniform stress distributions. Additionally, the calculator may not account for complex loading conditions or non-linear material behavior, which can affect the accuracy of the results.
What are the key factors that affect the design and operation of Seamless Full-Hemispherical Head ASME Pressure Vessels, and how can they be optimized?
The design and operation of Seamless Full-Hemispherical Head ASME Pressure Vessels are affected by several key factors, including material selection, wall thickness, internal pressure, and temperature. The material selection is critical, as it affects the strength, ductility, and corrosion resistance of the vessel. The wall thickness must be carefully calculated to ensure that it can withstand the internal pressure and stress levels. The internal pressure and temperature conditions must also be carefully controlled to prevent over-pressurization or overheating, which can lead to catastrophic failure. To optimize the design and operation of these vessels, finite element analysis and computational fluid dynamics can be used to simulate the stress and flow behavior, allowing for the optimization of the design parameters and operating conditions.
How can the Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator be applied to real-world engineering problems, and what are the potential benefits and challenges?
The Seamless Full-Hemispherical Head ASME Pressure Vessel Equations and Calculator can be applied to various real-world engineering problems, such as designing and optimizing pressure vessels for chemical processing and power generation applications. The equations and calculator can help engineers to quickly and accurately calculate the required wall thickness and stress levels, reducing the design time and cost. Additionally, the calculator can be used to validate and verify the design of existing pressure vessels, ensuring that they meet the required safety and performance criteria. However, the application of these equations and calculator requires a good understanding of the underlying assumptions and limitations, as well as the potential challenges associated with complex loading conditions and non-linear material behavior.
Deja una respuesta

Entradas Relacionadas