Mean Free Path of Gases Formulae and Calculator

The mean free path of gases is a fundamental concept in physics and chemistry, describing the average distance a gas molecule travels before colliding with another molecule. This distance is crucial in understanding various phenomena, such as gas diffusion, viscosity, and thermal conductivity. The mean free path is influenced by factors like temperature, pressure, and molecular size. To calculate this distance, several formulae are employed, taking into account the specific properties of the gas and the conditions it is in. A calculator can be used to simplify these complex calculations and provide accurate results.
Understanding the Mean Free Path of Gases: Formulae and Calculator
The mean free path of gases is a fundamental concept in physics and chemistry that describes the average distance a gas molecule travels between collisions with other molecules. This concept is crucial in understanding various phenomena, such as gas viscosity, diffusion, and conduction. The mean free path is calculated using the formula: λ = kT / (√2πd^2P), where λ is the mean free path! k is the Boltzmann constant, T is the temperature, d is the diameter of the gas molecule, and P is the pressure.
Definition and Importance of Mean Free Path
The mean free path is defined as the average distance traveled by a gas molecule between successive collisions. It is an important concept in understanding the behavior of gases, as it helps to explain various phenomena, such as gas viscosity and diffusion. The mean free path is also related to the collision frequency, which is the number of collisions a gas molecule undergoes per unit time.
Formulae for Calculating Mean Free Path
The formula for calculating the mean free path is λ = kT / (√2πd^2P), where λ is the mean free path, k is the Boltzmann constant, T is the temperature, d is the diameter of the gas molecule, and P is the pressure. This formula is derived from the kinetic theory of gases, which assumes that gas molecules are in constant random motion and undergo elastic collisions with each other.
Mean Free Path Calculator
A mean free path calculator is a tool used to calculate the mean free path of a gas using the formula λ = kT / (√2πd^2P). The calculator requires input values for the temperature, diameter of the gas molecule, and pressure. The calculator then uses these values to calculate the mean free path, which can be used to understand various phenomena, such as gas viscosity and diffusion.
Factors Affecting Mean Free Path
The mean free path is affected by several factors, including temperature, pressure, and diameter of the gas molecule. An increase in temperature or diameter of the gas molecule results in an increase in the mean free path, while an increase in pressure results in a decrease in the mean free path. The mean free path is also affected by the density of the gas, with a decrease in density resulting in an increase in the mean free path.
Applications of Mean Free Path
The mean free path has several applications in various fields, including physics, chemistry, and engineering. It is used to understand various phenomena, such as gas viscosity, diffusion, and conduction. The mean free path is also used in the design of vacuum systems, heat exchangers, and mass spectrometers.
| Gas | Temperature (K) | Pressure (Pa) | Diameter (m) | Mean Free Path (m) |
|---|---|---|---|---|
| Helium | 300 | 101325 | 2.18e-10 | 1.85e-7 |
| Oxygen | 300 | 101325 | 3.61e-10 | 6.53e-8 |
| Nitrogen | 300 | 101325 | 3.75e-10 | 5.81e-8 |
What is the formula for the mean free path of an ideal gas?

The formula for the mean free path of an ideal gas is given by λ = kT / (√2πd^2P), where λ is the mean free path, k is the Boltzmann constant, T is the temperature, d is the diameter of the gas molecules, and P is the pressure. This formula is derived from the kinetic theory of gases, which assumes that the gas molecules are in constant random motion and interact with each other through elastic collisions.
Derivation of the Mean Free Path Formula
The derivation of the mean free path formula involves several assumptions and simplifications, including the assumption that the gas molecules are spherical and that the collisions between them are elastic. The formula is derived by considering the average distance traveled by a gas molecule between collisions, which is related to the mean free time and the average velocity of the molecules. The resulting formula is a simple expression that depends on the temperature, diameter of the gas molecules, and pressure of the gas.
- The mean free path is the average distance traveled by a gas molecule between collisions.
- The mean free time is the average time between collisions, which is related to the mean free path and the average velocity of the molecules.
- The average velocity of the molecules is a function of the temperature and the mass of the molecules.
Importance of the Mean Free Path in Gas Dynamics
The mean free path is an important parameter in gas dynamics, as it determines the transport properties of the gas, such as the viscosity and thermal conductivity. The mean free path also plays a crucial role in the behavior of gases at high temperatures and low pressures, where the collisions between molecules are less frequent. In these conditions, the mean free path can be comparable to or even larger than the size of the container, which can lead to non-equilibrium behavior and deviations from the ideal gas law.
- The viscosity of a gas is related to the mean free path and the average velocity of the molecules.
- The thermal conductivity of a gas is also related to the mean free path and the average velocity of the molecules.
- The behavior of gases at high temperatures and low pressures is strongly influenced by the mean free path.
Relationship Between Mean Free Path and Gas Properties
The mean free path is inversely proportional to the pressure of the gas and directly proportional to the temperature. This means that as the pressure increases, the mean free path decreases, and as the temperature increases, the mean free path increases. The mean free path is also inversely proportional to the square of the diameter of the gas molecules, which means that larger molecules have a shorter mean free path.
- The pressure of a gas affects the mean free path, with higher pressures resulting in a shorter mean free path.
- The temperature of a gas affects the mean free path, with higher temperatures resulting in a longer mean free path.
- The diameter of the gas molecules affects the mean free path, with larger molecules resulting in a shorter mean free path.
Applications of the Mean Free Path in Physics and Engineering
The mean free path has important applications in physics and engineering, including the design of vacuum systems, the study of gas dynamics, and the development of new materials. The mean free path is also used to model the behavior of gases in complex systems, such as turbines and heat exchangers. In these systems, the mean free path can be used to predict the performance and optimize the design.
- The design of vacuum systems requires a understanding of the mean free path and its relationship to the pressure and temperature of the gas.
- The study of gas dynamics relies heavily on the mean free path, which is used to model the behavior of gases in complex systems.
- The development of new materials often involves the use of thin films and nanostructures, which can be affected by the mean free path of the gas molecules.
Limitations and Assumptions of the Mean Free Path Formula
The mean free path formula is based on several assumptions and simplifications, including the assumption that the gas molecules are spherical and that the collisions between them are elastic. The formula is also limited to ideal gases, which means that it may not be applicable to real gases that exhibit non-ideal behavior. Additionally, the formula assumes that the gas is in thermal equilibrium, which may not always be the case in real systems.
- The assumptions of the mean free path formula, such as the assumption of spherical molecules, can limit its applicability to real systems.
- The simplifications of the mean free path formula, such as the assumption of elastic collisions, can also limit its accuracy.
- The limitations of the mean free path formula, such as its restriction to ideal gases, can make it difficult to apply to real systems.
What is the mean free path of a gas particle?
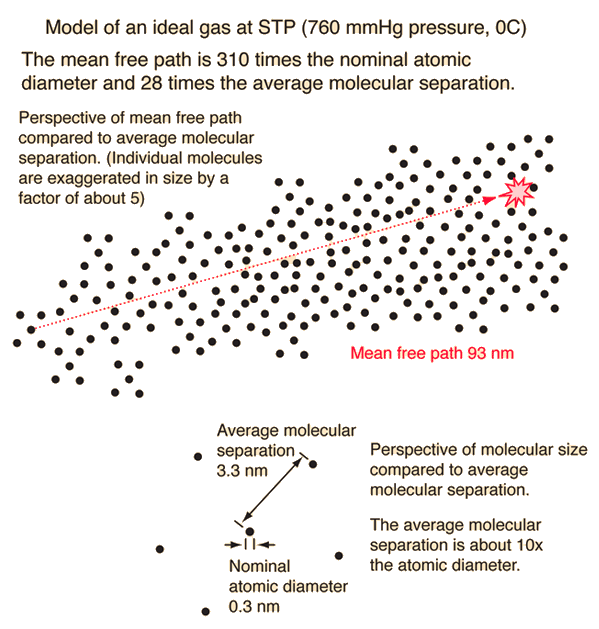
The mean free path of a gas particle is the average distance it travels between collisions with other particles. This concept is crucial in understanding the behavior of gases and is used to describe the transport properties of gases, such as diffusion and viscosity. The mean free path is an important parameter in kinetic theory, which is a theoretical framework used to study the behavior of gases.
Definition and Formula
The mean free path is defined as the average distance a gas particle travels between collisions with other particles. It can be calculated using the formula: λ = 1 / (√2 π d^2 n), where λ is the mean free path, d is the diameter of the gas particle, and n is the number density of the gas. The mean free path depends on the temperature and pressure of the gas, as well as the size and shape of the particles.
- The mean free path is inversely proportional to the square of the particle diameter.
- The mean free path is inversely proportional to the number density of the gas.
- The mean free path is directly proportional to the temperature of the gas.
Factors Affecting Mean Free Path
The mean free path of a gas particle is affected by several factors, including the temperature, pressure, and composition of the gas. At higher temperatures, the particles have more energy and are able to travel farther between collisions, resulting in a longer mean free path. At higher pressures, the particles are packed more closely together, resulting in a shorter mean free path.
- Temperature is a key factor in determining the mean free path, as it affects the kinetic energy of the particles.
- Pressure also plays a crucial role, as it affects the density of the gas.
- Composition of the gas can also affect the mean free path, as different particles have different sizes and shapes.
Importance in Kinetic Theory
The mean free path is a fundamental concept in kinetic theory, which is used to study the behavior of gases. It is used to calculate the transport properties of gases, such as diffusion and viscosity. The mean free path is also used to understand the behavior of gases in different situations, such as in vacuums or at high pressures.
- The mean free path is used to calculate the diffusion coefficient of a gas.
- The mean free path is used to calculate the viscosity of a gas.
- The mean free path is used to understand the behavior of gases in nonequilibrium situations.
Applications in Real-World Systems
The mean free path has numerous applications in real-world systems, including in the design of engines, pumps, and turbines. It is also used in the study of atmospheric and space phenomena, such as the behavior of gases in the atmosphere and the propagation of sound waves.
- The mean free path is used in the design of aerodynamic systems, such as aircraft and missiles.
- The mean free path is used in the study of atmospheric phenomena, such as weather patterns and climate change.
- The mean free path is used in the study of space phenomena, such as the behavior of gases in space.
Relationship to Other Physical Properties
The mean free path is related to other physical properties of gases, such as pressure, temperature, and density. It is also related to the behavior of gases in different situations, such as in equilibrium and nonequilibrium situations.
- The mean free path is inversely proportional to the pressure of the gas.
- The mean free path is directly proportional to the temperature of the gas.
- The mean free path is related to the density of the gas, as it affects the number density of the particles.
What is the mean free path of electrons in a gas?
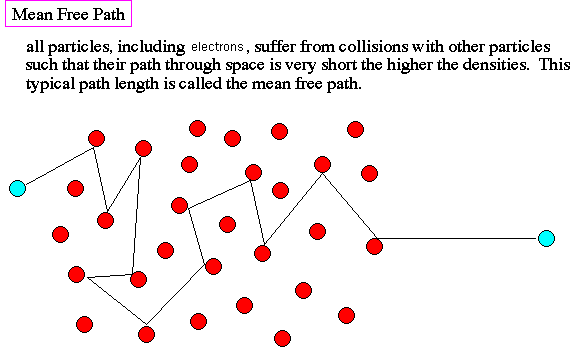
The mean free path of electrons in a gas is the average distance an electron travels between collisions with gas molecules. This concept is crucial in understanding the behavior of plasmas and gases in various fields, including physics, chemistry, and engineering.
Definition and Importance
The mean free path is defined as the average distance an electron travels before experiencing a collision with a gas molecule. This distance is a critical parameter in determining the transport properties of plasmas and gases, such as electrical conductivity and thermal conductivity. The mean free path depends on the density of the gas, the temperature, and the cross-sectional area of the gas molecules. Some key factors that affect the mean free path include:
- The number density of the gas molecules, which affects the frequency of collisions.
- The temperature of the gas, which influences the kinetic energy of the electrons and the gas molecules.
- The cross-sectional area of the gas molecules, which determines the probability of collisions.
Calculation Methods
The mean free path can be calculated using various methods, including kinetic theory and Monte Carlo simulations. The kinetic theory approach involves solving the Boltzmann equation, which describes the distribution function of the electrons in the gas. The Monte Carlo simulations involve tracking the trajectories of individual electrons and gas molecules to estimate the mean free path. Some key parameters that are required for these calculations include:
- The mass and charge of the electrons and gas molecules.
- The density and temperature of the gas.
- The cross-sectional area of the gas molecules.
Factors Affecting the Mean Free Path
Several factors can affect the mean free path of electrons in a gas, including the pressure, temperature, and composition of the gas. The mean free path is inversely proportional to the pressure of the gas, meaning that higher pressures result in shorter mean free paths. The temperature of the gas also affects the mean free path, as higher temperatures increase the kinetic energy of the electrons and the gas molecules, leading to more frequent collisions. Some key factors that affect the mean free path include:
- The pressure of the gas, which affects the density of the gas molecules.
- The temperature of the gas, which influences the kinetic energy of the electrons and the gas molecules.
- The composition of the gas, which affects the cross-sectional area of the gas molecules.
Applications in Plasma Physics
The mean free path is a crucial parameter in plasma physics, as it determines the transport properties of plasmas, such as electrical conductivity and thermal conductivity. Understanding the mean free path is essential for designing and optimizing plasma devices, such as plasma etchers and plasma sources. Some key applications of the mean free path in plasma physics include:
- Plasma etching, where the mean free path affects the etching rate and uniformity.
- Plasma sources, where the mean free path influences the ionization efficiency and stability.
- Plasma diagnostics, where the mean free path is used to estimate the density and temperature of the plasma.
Comparison with Other Transport Properties
The mean free path is related to other transport properties, such as electrical conductivity and thermal conductivity, which are also critical in understanding the behavior of plasmas and gases. The mean free path is inversely proportional to the collision frequency, which affects the electrical conductivity and thermal conductivity of the gas. Some key relationships between the mean free path and other transport properties include:
- The electrical conductivity, which is affected by the mean free path and the collision frequency.
- The thermal conductivity, which is influenced by the mean free path and the temperature of the gas.
- The viscosity, which is related to the mean free path and the density of the gas.
Frequently Asked Questions (FAQs)
What is the Mean Free Path of Gases and its importance in physics?
The mean free path of gases is a fundamental concept in physics and chemistry, which refers to the average distance a gas molecule travels between collisions with other molecules. This concept is crucial in understanding the behavior of gases and their interactions with other substances. The mean free path is an important factor in determining the transport properties of gases, such as viscosity, thermal conductivity, and diffusion. By understanding the mean free path, scientists can better comprehend the behavior of gases in various environments, including atmospheric conditions, chemical reactions, and industrial processes.
How is the Mean Free Path of Gases calculated using formulae and calculators?
The mean free path of gases can be calculated using various formulae, which take into account the properties of the gas, such as its density, temperature, and pressure. One commonly used formula is the kinetic theory equation, which relates the mean free path to the mean velocity of the gas molecules and the collision frequency. Calculators and computer simulations can also be used to calculate the mean free path, providing a more accurate and efficient way to determine this important parameter. These calculators and simulations often utilize algorithms and models that account for the complex interactions between gas molecules, allowing for a more precise calculation of the mean free path.
What are the key factors that affect the Mean Free Path of Gases?
The mean free path of gases is influenced by several key factors, including temperature, pressure, and density. As the temperature of a gas increases, the mean free path decreases, due to the increased velocity of the gas molecules. Conversely, as the pressure of a gas increases, the mean free path also decreases, due to the increased frequency of collisions between molecules. The density of a gas also plays a crucial role, as it affects the number of molecules present in a given volume, which in turn affects the mean free path. Other factors, such as the size and shape of the gas molecules, can also influence the mean free path, making it a complex and multifaceted phenomenon.
How is the Mean Free Path of Gases used in real-world applications and industries?
The mean free path of gases has numerous practical applications in various industries, including aerospace, chemical engineering, and materials science. In aerospace engineering, the mean free path is used to design more efficient rocket engines and heat shields, which must withstand the harsh conditions of space. In chemical engineering, the mean free path is used to optimize chemical reactions and processes, such as catalysis and separation. In materials science, the mean free path is used to understand the properties of nanomaterials and thin films, which have unique electronic and thermal properties. By understanding and applying the concept of mean free path, scientists and engineers can develop new technologies and improve existing ones, leading to innovations and advances in various fields.
Deja una respuesta

Entradas Relacionadas