Una de las relaciones fundamentales más importantes en la fabricación ajustada es la relación entre el inventario, el rendimiento y el tiempo de entrega. El inventario y el rendimiento suelen ser fáciles de medir. El plazo de entrega, sin embargo, es más difícil. Debería tomarse el tiempo cuando una parte ingresa al sistema y luego tomar el tiempo nuevamente cuando una parte abandona el sistema. Por suerte, el tiempo de entrega se puede calcular de manera fácil y precisa utilizando la Ley de Little, una de las leyes más fundamentales en la fabricación ajustada (y también en muchos otros lugares).
La Ley de Little se publicó por primera vez alrededor de 1954. Lleva el nombre de John Little (un profesor del MIT y no uno de los hombres felices de Robin Hood 🙂). No inventó la ley, pero fue el primero en demostrar matemáticamente su validez universal en 1961.
Las variables
Primero, primero expliquemos las variables. A lo largo de esta publicación, usaré un pago en el supermercado como ejemplo, suponiendo que todos ustedes hayan esperado en línea en el momento del pago. Por lo tanto, nuestro sistema de ejemplo es el sistema de pago, definido como el sistema que incluye a todos los clientes que esperan en línea o que se procesan (pero que aún no compran productos).
Inventario
El inventario es simplemente el número de partes en el sistema observado. También podría llamarlo WIP (Work in Progress). Para nuestro proceso de pago en el supermercado, el inventario sería la cantidad de personas que esperan en la fila, incluido el cliente que se atiende actualmente (pero no el cajero, ese sería el proceso).
El inventario suele ser bastante fácil de medir. Simplemente cuente el número de partes en el sistema, ya sea a mano o buscando sus datos ERP. Puede usar el inventario actual si está interesado en un estado actual del sistema. También puede usar el inventario promedio durante un período más largo si desea analizar el comportamiento promedio del sistema.
Rendimiento
El rendimiento es el número promedio de partes completadas en un tiempo dado. Tomando nuevamente el ejemplo de un supermercado, podría medirse en clientes por hora.
El rendimiento también es bastante fácil de medir. Verifica cuántas piezas ha producido durante un período de tiempo. Dividir el número de partes por el tiempo total le da el rendimiento.
En cuanto al rendimiento, de nuevo, hay diferentes formas de medirlo. Podrías mirar un período más largo, incluidos los fines de semana y los horarios fuera del turno (es decir, ¿cuántas partes produjiste durante el mes?). Alternativamente, solo podría observar durante las horas de trabajo reales (es decir, ¿cuántas piezas produjo durante un turno de 8 horas?). Ambos son posibles. Dependiendo de cuál use, obtendrá el tiempo de rendimiento en horas de trabajo u horas totales, incluido el tiempo libre.
Tiempo de espera
El tiempo de entrega es el tiempo que tarda una parte en pasar completamente por el sistema (es decir, es el tiempo entre la entrada y la salida del proceso). En el ejemplo de las cajas de los supermercados, es el momento desde el momento en que comienza a esperar en línea hasta que recoge sus productos y se va.
El tiempo de entrega es difícil de medir directamente. En un supermercado, puede hacer que todos midan su propio tiempo de espera. Para las partes físicas, sin embargo, alguien tendría que medirlo. En realidad, esto es poco práctico.
Sin embargo, el tiempo de entrega es un valor importante en la fabricación. Un plazo de entrega más largo significa que necesitará más tiempo para implementar los cambios.
Ley de Little
La Ley
La Ley de Little es en realidad bastante simple. Hay tres variables, a menudo etiquetadas de la siguiente manera:
La Ley de Little es entonces la relación muy simple como se muestra a continuación.
Sin embargo, en aras de la claridad, prefiero escribirlo en su totalidad. Por lo tanto:
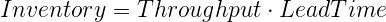
Por lo tanto, para determinar el tiempo de entrega que calcula:
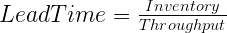
Y finalmente, para determinar el rendimiento que calcula:
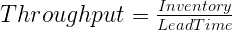
Los supuestos subyacentes
A menudo, en la academia, puede encontrar resultados de investigación muy jactanciosos, excepto que si lee detenidamente los supuestos, descubre que se aplica solo a una situación muy especial y poco realista. Con bastante frecuencia, estas limitaciones hacen que los resultados de la investigación sean inutilizables en la práctica.
La Ley de Little, sin embargo, solo tiene dos supuestos principales. Primero, necesitas tener un sistema estable sin grandes cambios. En otras palabras, las tres variables involucradas (inventario, rendimiento y tiempo de entrega) no cambian significativamente mientras se observan. Asuma nuevamente que tiene un supermercado con un cajero. Usando Little’s Law, calcula el tiempo de espera estimado en función de la velocidad del cajero y el número de personas en la cola. Sin embargo, si se abre una segunda línea de pago, la velocidad del sistema se duplica. Por lo tanto, su cálculo ya no es válido, ya que la velocidad del sistema se ha duplicado. Del mismo modo, si la cola se alarga porque llegan más personas que se van, la Ley de Little ya no da el tiempo de espera promedio. Por lo tanto, las tasas de llegada y salida deben ser similares.
Segundo, Las unidades utilizadas para el inventario, el rendimiento y el tiempo de entrega deben ser consistentes. Medir el rendimiento en lotes por hora, el inventario en artículos individuales y el tiempo de entrega en días arruinarán sus cálculos, a menos que convierta los valores en unidades consistentes.
En la práctica, sin embargo, ambos supuestos son supuestos muy razonables. En primer lugar, la mayoría de los sistemas de fabricación no cambian drásticamente en poco tiempo, incluso si simplemente actualiza los valores de la fórmula y obtiene los nuevos números. Con respecto a las unidades, el conocimiento básico de las matemáticas y el sentido común puede evitar fácilmente este problema. Por lo tanto, ¡Little’s Law tiene una validez casi universal y es altamente aplicable en la práctica!
Lo que no es relevante
La belleza de la Ley de Little son todos los factores que no importan. Esta universalidad hace que la Ley de Little sea extremadamente práctica en las operaciones cotidianas en el taller.
Algunos ejemplos de cálculos
Hagamos algunos cálculos de muestra. Asumir una línea de caja de supermercado. ¿Cuánto tiempo tiene que un cliente esperar en la caja del supermercado para el siguiente ejemplo:
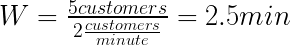
Por lo tanto, un cliente espera un promedio de 2.5 minutos en línea. Expandamos esto para todo el supermercado. ¿Cuánto tiempo pasa el cliente promedio en el supermercado? Asumamos:
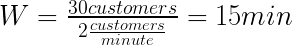
Por lo tanto, el cliente promedio pasa 15 minutos en el supermercado, de los cuales pasa 12.5 minutos comprando y 2.5 minutos en la caja. Si observamos a las personas más de cerca, también veríamos que 25 de ellos están comprando y 5 están esperando en la caja.
Hagamos un ejemplo de fabricación . Cuál es el duración promedio que una parte gasta en el almacén de productos terminados (es decir, ¿cuál es nuestro alcance en productos terminados)?
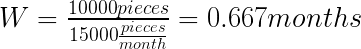
Por lo tanto, la pieza promedio pasa dos tercios de un mes en el almacén. Veamos el plazo de entrega de todo el flujo de material:
Por lo tanto, una parte tarda aproximadamente 1 mes en pasar por todo el sistema. Ahora supongamos que tenemos un sistema kanban. ¿Cuánto tiempo tarda un kanban en completar el ciclo? Suponga que un kanban representa 100 piezas, y hay en promedio 50 kanbans esperando la producción.
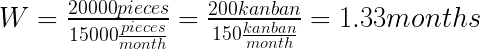
Por lo tanto, toma 1.33 meses antes de que un kanban complete un ciclo completo.
También puede usar la Ley de Little para el procesamiento continuo como, por ejemplo, productos químicos. Vamos a calcular cuánto tiempo permanece el agua en el lago más grande de Estados Unidos, el Lago Superior, antes de que salga del lago.
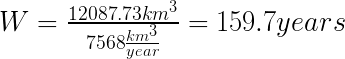
Por lo tanto, el agua permanece en el Lago Superior durante casi 160 años antes de que fluya. Más de la mitad del agua en el lago ya estaba allí cuando Abraham Lincoln era presidente 🙂.
Por qué es relevante
La Ley de Little es casi siempre válida y muy fácil de calcular. También muestra la relación de los dos factores que influyen en el tiempo de entrega: inventario y rendimiento. El siguiente gráfico muestra esta relación en términos relativos.
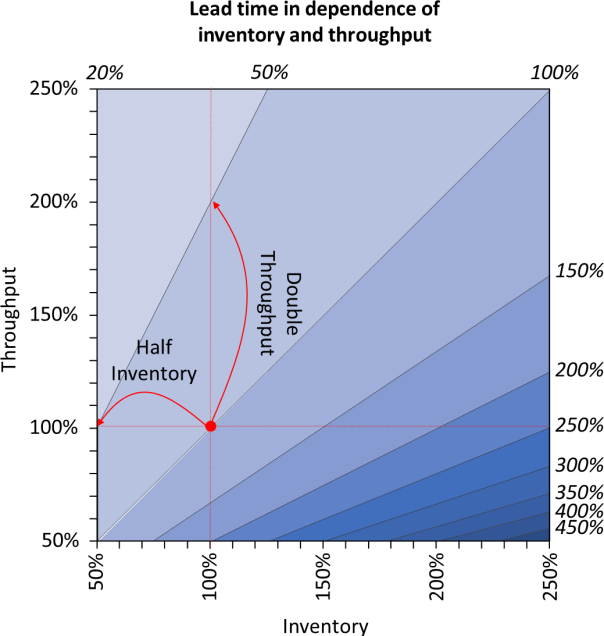Por lo tanto, si desea reducir su tiempo de espera a la mitad, deberá duplicar su rendimiento o reducir a la mitad su inventario. Ambos lograrían los mismos resultados. Sin embargo, duplicar el número de piezas producidas en un momento dado es probablemente bastante difícil y costoso en la práctica. Reducir a la mitad el inventario suele ser mucho más fácil. Además, si reduce a la mitad su inventario, incluso puede recuperar el dinero vendiendo temporalmente más de lo que compra o produce.
Por lo tanto, la Ley de Little es otra justificación matemática para el impulso en la producción ajustada para reducir el inventario, y la ventaja de la producción de extracción y su límite fijo en WIP. Pero, por favor, mantenga suficiente inventario para que su sistema funcione sin problemas, o será más costoso que antes.
Espero que este artículo sea interesante para usted y lo ayude con su trabajo diario de mejorar su sistema . Ahora, sal, calcula tu tiempo de entrega y Organiza tu industria!
PD: Esta es mi publicación número 100 en AllAboutLean.com. Gracias por leer, seguir y comentar 🙂
